Метод координат в пространстве

Прямоугольная система координат в пространстве
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждом из них выбрано направление(оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
Рассмотрим рисунок

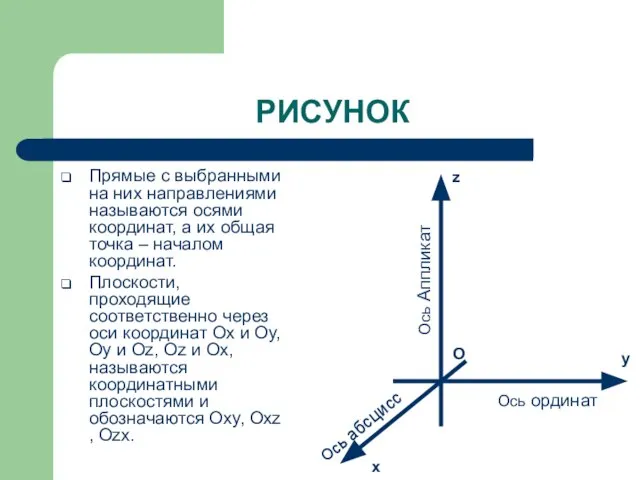
РИСУНОК
Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат.
Плоскости, проходящие соответственно через оси координат Ох и Оy, Oу и Оz, Oz и Ox, называются координатными плоскостями и обозначаются Oxy, Oхz , Ozх.
Ось Аппликат
Ось абсцисс
Ось ординат
y
z
O
x

Определение луча на координатной плоскости.
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью.

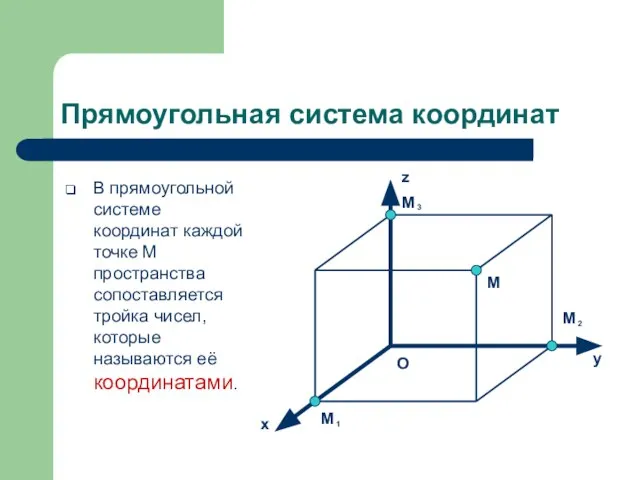
Прямоугольная система координат
В прямоугольной системе координат каждой точке M пространства сопоставляется тройка чисел, которые называются её координатами.
y
z
x
M
1
M
2
M
3
M
O

Нахождение точки на координатной плоскости.
Если, например, точка M лежит на координатной плоскости или на оси координат, то некоторые её координаты равны нулю. Так, если M принадлежит Oxy, то аппликата точка M равна нулю: z=0. Аналогично если M принадлежит Oхz, то y=0, а если M принадлежит Oyz, то x=0. Если M принадлежит Ox, то ордината и аппликата точки M равна нулю: y=0 и z=0. Если M принадлежит Oy, то x=0 и z=0; если M принадлежит Oz, то x=0 и y=0. Все три координаты начала координат равны нулю: О (0;0;0). Напиши координаты для точек A, B, C, D, E, F на рисунке следующего слайда.

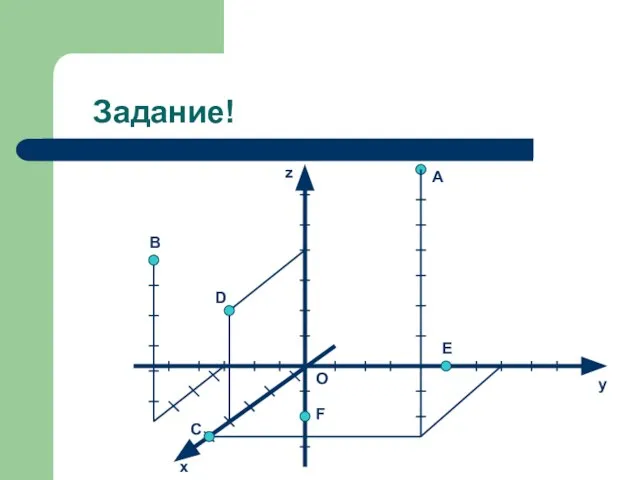
Задание!
B
C
O
E
F
D
z
y
x
A

Ответы.
A(5; 4; 10),
B(4; -3; 6),
C(5; 0; 0),
D(4; 0; 4),
E(0; 5; 0),
F(0; 0; -2).
Сравни свои ответы.

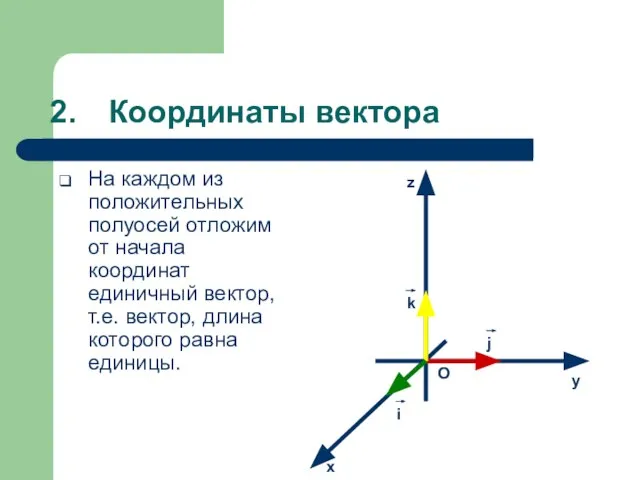
Координаты вектора
На каждом из положительных полуосей отложим от начала координат единичный вектор, т.е. вектор, длина которого равна единицы.
j
k
i
y
z
x
O

Разложение по координатным векторам
Любой вектор a можно разложить по координатным векторам, т.е. представить в виде
а = xi + yj + zk
Причем коэффициенты разложения x, y, z определяются единственным образом.

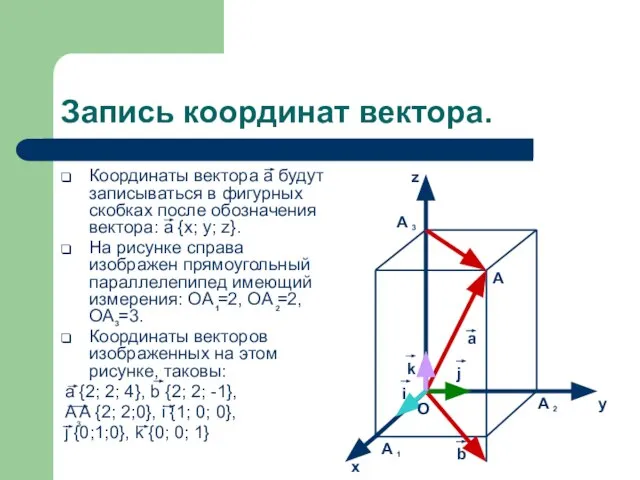
Запись координат вектора.
Координаты вектора а будут записываться в фигурных скобках после обозначения вектора: а {x; y; z}.
На рисунке справа изображен прямоугольный параллелепипед имеющий измерения: OA =2, OA =2, OA =3.
Координаты векторов изображенных на этом рисунке, таковы:
a {2; 2; 4}, b {2; 2; -1},
A A {2; 2;0}, i {1; 0; 0},
j {0;1;0}, k {0; 0; 1}
A
A
A
A
O
y
x
z
a
j
i
k
b
3
2
1
1
2
3
3

Нулевой вектор и равные вектора
Так как нулевой вектор можно представить в виде 0 = 0i + 0j + 0k, то все координаты нулевого вектора равны нулю.
Координаты равных векторов соответственно равны, т.е. если векторы
a {x ; y ; z } и b {x ; y ; z } равны, то x =x , y =y и z =z .
1
1
1
2
2
2
1
2
1
2
1
2

Правила нахождения суммы, разности и произведения на данное число.
Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a + b имеет координаты
{x +x ; y +y ; z +z }
1
2
1
2
1
2
2
2
2
1
1
1

Правило №2
Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a – b имеет координаты
{x –x ; y –y ; z –z }
1
2
1
2
1
2
1
2
1
1
2
2

Правило №3
Каждая координата произведения вектора на число равна произведение соответствующей координаты вектора на это число. Если a {x; y; z } – данный вектор, α - данное число, то вектор αa имеет координаты
{ x; y; z}
α
α
α

Связь между координатами векторов и координатами точек.
Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором данной точки.
Координаты любой точки равны соответствующим координатам её радиус-вектора.
Каждая координата вектора равна разности соответствующих координат его конца и начала.

Простейшие задачи в координатах
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Длина вектора a {x; y; z} вычисляется по формуле
|a| = √x² + y² + z²

Расстояние между точками
Расстояния между точка M (x ; y ; z ) и
M (x ; y ; z ) вычисляется по формуле
d = √(x – x )² + (y – y )² + (z – z )²
1
2
2
2
2
1
1
1
2
1
2
1
2
1

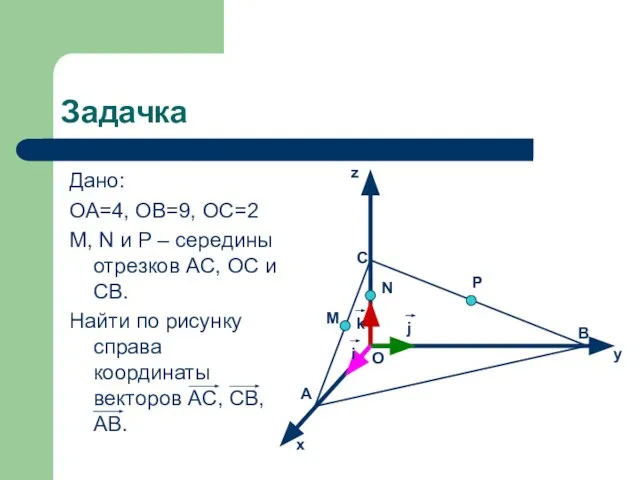
Задачка
Дано:
ОА=4, ОВ=9, ОС=2
M, N и P – середины отрезков AC, OC и CB.
Найти по рисунку справа координаты векторов AC, CB, AB.
P
B
y
N
j
i
k
M
O
C
A
x
z

Решение:
AC = AO + OC = 4i + 2k, AC {-4; 0; 2}
CB = CO + OB = 2k + 9j, CB {0; 9; 2}
AB = AO + OB = -4i + 9j, AB {-4; 7; 0}