Методическая разработка темы: «Показательная функция»

Содержание
Показательная функция
Показательные уравнения
Показательные неравенства
Типовые задачи
Тесты
Домашняя контрольная работа

Показательная функция
График.
Определение
Свойства
Содержание

Определение
Показательная функция – это функция вида ,
где x – переменная,
- заданное число, >0, ≠1.
Примеры:
⮍ к теме

Свойства показательной функции
Область определения:
все действительные числа
Множество значений:
все положительные числа
При > 1 функция возрастающая;
при 0 < < 1 функция убывающая.
D(y) = R;
E(y) = (0; + ∞);
⮍ к теме

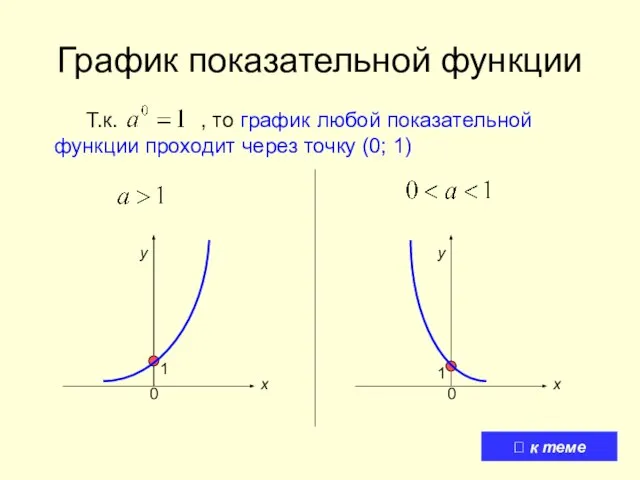
График показательной функции
Т.к. , то график любой показательной функции проходит через точку (0; 1)
1
1
х
х
у
у
0
0
⮍ к теме

Показательные уравнения
Определение
Простейшие уравнения
Способы решения сложных уравнений
Содержание

Определение
Уравнение, в котором переменная содержится в показателе степени, называется показательным.
Примеры:
⮍ к теме

Простейшее показательное уравнение – это уравнение вида
Простейшее показательное уравнение решается с использованием свойств степени.
⮍ к теме

Способы решения сложных показательных уравнений.
Вынесение за скобки степени с меньшим показателем
Замена переменной
Деление на показательную функцию
⮍ к теме

Вынесение за скобки степени с меньшим показателем
Данный способ используется, если соблюдаются два условия:
1) основания степеней
одинаковы;
2) коэффициенты перед
переменной одинаковы
Например:
решение

Замена переменной
При данном способе показательное уравнение сводится к квадратному.
Способ замены переменной используют, если
показатель одной из степеней в 2 раза больше, чем
у другой.
Например:
3 2x – 4 · 3 х – 45 = 0
коэффициенты перед
переменной противоположны.
Например:
2 2 - х – 2 х – 1 =1
б)
а) основания степеней одинаковы;
решение
решение

Деление на показательную функцию
Данный способ используется, если основания степеней разные.
а) в уравнении вида ax = bx делим на bx
Например: 2х = 5х | : 5x
б) в уравнении A a2x + B (ab)x + C b2x = 0
делим на b2x.
Например:
3⋅25х - 8⋅15х + 5⋅9х = 0 | : 9x
решение
решение

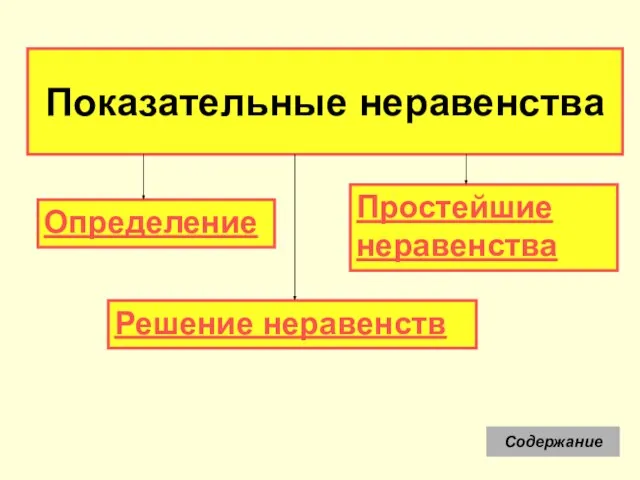
Показательные неравенства
Определение
Простейшие неравенства
Решение неравенств
Содержание

Определение
Показательные неравенства –
это неравенства, в которых неизвестное содержится в показателе степени.
Примеры:
⮍ к теме

Простейшие показательные неравенства – это неравенства вида:
где a > 0, a ≠ 1, b – любое число.
⮍ к теме

При решении простейших неравенств используют свойства возрастания или убывания показательной функции. Для решения более сложных показательных неравенств используются те же способы, что и при решении показательных уравнений.
⮍ к теме

Типовые задачи
Показательная функция
Показательные уравнения
Показательные неравенства
Содержание

Показательная функция
Построение графика
Сравнение чисел с использованием свойств показательной функции
Сравнение числа с 1
а) аналитический способ;
б) графический способ.
? типовые задачи

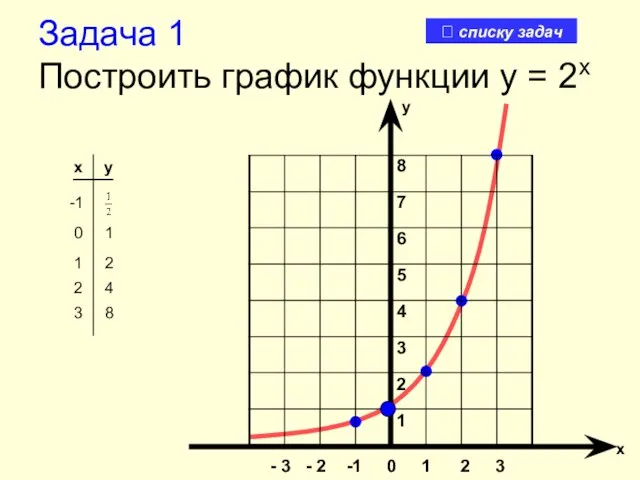
Задача 1
Построить график функции y = 2x
x
y
-1
8
7
6
5
4
3
2
1
- 3 - 2 -1 0 1 2 3
х
у
3 8
2 4
1 2
0 1
? списку задач

Задача 2
Сравнить числа
Решение
Ответ:
? списку задач

Задача 3
Сравнить число с 1.
Решение
-5 < 0
Ответ:
? списку задач

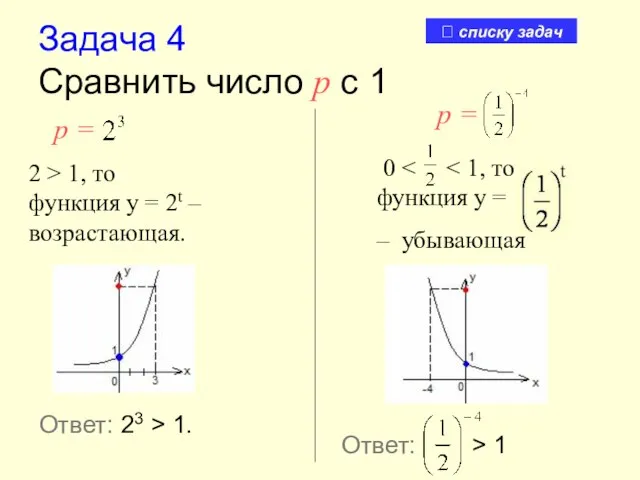
Задача 4
Cравнить число р с 1
р =
2 > 1, то функция у = 2t – возрастающая.
0 < < 1, то
функция у =
– убывающая
Ответ: 23 > 1.
Ответ:
> 1
? списку задач
р =

Показательные уравнения
Простейшие показательные уравнения
Уравнения, решаемые вынесением за скобки степени с меньшим показателем
Уравнения, решаемые заменой переменной
случай 1;
случай 2.
Уравнения, решаемые делением на показательную функцию
случай 1;
случай 2.
? типовые задачи

Простейшие показательные уравнения
Ответ: - 5,5.
Ответ: 0; 3.
? списку задач

Вынесение за скобки степени с меньшим показателем
Ответ: 5
x + 1 - (x - 2) =
= x + 1 – x + 2 = 3
? списку задач
⮍ к теории

Замена переменной (сл.1)
основания степеней одинаковы, показатель одной из степеней в 2 раза больше, чем у другой .
3 2x – 4 · 3 х – 45 = 0
t = 3x (t > 0)
t 2 – 4t – 45 = 0
По т. Виета: t1· t 2 = - 45; t1+ t 2 =4
t1 = 9; t 2 = - 5 – посторонний корень
3x = 9; 3x = 32; x = 2.
Ответ: 2
? списку задач
⮍ к теории

Замена переменной (сл. 2)
Основания степеней одинаковы,
коэффициенты перед переменной противоположны.
По т. Виета:
- посторонний корень
Ответ: 1
? списку задач
⮍ к теории

Деление
на показательную функцию
Ответ: 0
? списку задач
⮍ к теории

Деление
на показательную функцию
Ответ: 0; 1.
? списку задач
⮍ к теории

Простейшие показательные неравенства
Двойные неравенства
Неравенства, решаемые вынесением за скобки степени с меньшим показателем
Неравенства, решаемые заменой переменной
Показательные неравенства
? типовые задачи

Простейшие
показательные неравенства
? списку задач

Двойные неравенства
Ответ: (- 4; -1).
3 > 1, то
? списку задач

Решение
показательных неравенств
Метод: Вынесение за скобки степени с меньшим
показателем
Ответ: х >3
3 > 1, то
: 10
? списку задач

Решение показательных неравенств
Метод: Замена переменной
Ответ: х < -1.
3>1, то
? списку задач

Тесты по темам:
Показательная функция и её свойства
Показательные уравнения
Показательные неравенства
Содержание