Методы оптимальных решений. Решение прикладных задач

Решение прикладных задач
Дано словесное описание задачи. Привести ее табличное и математическое описание: целевая функция, система ограничений

Задача №1.
Завод выпускает два вида строительных материалов: жидкое стекло и пенопласт. Трудозатраты на производство 1 т. стекла – 20 ч., пенопласта – 10ч. На заводе работает 10 рабочих по 40 часов в неделю. Оборудование позволяет производить не более 15 т. стекла и 30 т. пенопласта в неделю. Прибыль от реализации 1 т. стекла – 50 руб., 1 т. пенопласта – 40 руб. Сколько материалов каждого вида необходимо произвести для того, чтобы получить максимальную прибыль.
Решение:
Пусть завод выпускает т. стекла, т. пенопласта, тогда по условию задачи мы имеем систему неравенств - ограничений:

Прибыль данного предприятия от реализации производимой продукции составит
руб.
Итак, мы получили следующую задачу линейного программирования. Руководству завода необходимо определить такие и объемы производимой продукции, чтобы выполнялись условия-ограничения:

и прибыль предприятия, задаваемая функцией ,
была бы максимальной.
.

Задача №2
Предприятие располагает ресурсами сырья и рабочей силы, необходимыми для производства двух видов продукции. Запас сырья составляет 120 т., трудозатрат – 400 часов. На единицу первого продукта необходимо затратить 3 т. сырья, на единицу второго – 5 т. На единицу первого продукта тратится 14 ч., второго – 12 ч. Прибыль от реализации единицы первого продукта равна 30 тыс./т., второго продукта – 35 тыс./т. Чему равна максимальная прибыль
Решение:
Пусть предприятие выпускает единиц продукции I – го вида, единиц продукции II – го вида. Тогда по условию задачи мы имеем систему неравенств - ограничений:

Прибыль данного предприятия от реализации производимой продукции
составит тыс./т.
Итак, мы получили следующую задачу линейного программирования. Руководству предприятия необходимо определить такие и объемы производимой продукции, чтобы выполнялись условия-ограничения:

и прибыль предприятия, задаваемая функцией ,
была бы максимальной.

Задача №3
Предприятие производит продукцию двух видов, используя для этого ресурсы трех видов. Известна технологическая матрица и вектор ресурсов . Элемент технологической матрицы соответствует ресурсу , необходимому для производства единицы продукта .
Технологическая матрица ,
вектор
Пусть предприятие выпускает
единиц продукции I – го вида,
единиц продукции II – го вида,
- система ограничений.
Решение:

Задача №4
Предприятие имеет ресурсы А и Б в количестве 240 и 120 единиц соответственно. Ресурсы используются при выпуске двух видов изделий, причем расход на изготовление одного изделия первого вида составляет 3 единицы ресурса А и 2 единицы ресурса В, на изготовление одного изделия второго вида – 2 единицы ресурса А и 2 единицы ресурса В. Прибыль от реализации одного изделия первого вида – 20 руб., второго вида – 30 руб. Ресурс В должен быть использован полностью, изделий первого вида надо выпустить не менее чем изделий второго вида.
Решение:
Пусть предприятие выпускает единиц изделий I – го вида, единиц изделий II – го вида. Тогда по условию задачи мы имеем систему неравенств - ограничений:

Прибыль данного предприятия от реализации производимой продукции
составит руб.
Итак, мы получили следующую задачу линейного программирования. Руководству предприятия необходимо определить такие и объемы производимых изделий, чтобы выполнялись условия-ограничения:
и прибыль предприятия, задаваемая функцией
была бы максимальной.

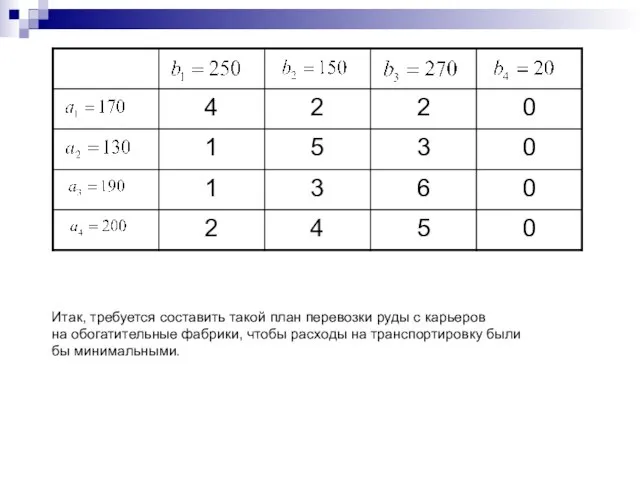
Задача №5
Компания, занимающаяся добычей руды, имеет четыре карьера. Производительность карьеров соответственно 170, 130, 190, 200 тыс. т. ежемесячно. Руда направляется на три обогатительные фабрики, мощности которых соответственно 250, 150, 270 тыс. т. в месяц. Транспортные затраты на перевозку 1тыс. т. руды с карьеров на фабрики заданы таблично. Сформировать таблицу транспортных затрат самостоятельно. Составить математическую модель задачи.

Решение:
Итак, определим модель транспортной задачи, для этого проверим условие.
Сравнивая суммарную производительность карьеров
и суммарные мощности обогатительных фабрик потребность
в руде, установим, является ли модель транспортной задачи, заданная этой таблицей,
открытой или закрытой.
(тыс. т.).
(тыс. т.).
с нулевыми затратами на перевозку. В результате чего получаем следующую модель
транспортной задачи.

Итак, требуется составить такой план перевозки руды с карьеров
на обогатительные фабрики, чтобы расходы на транспортировку были
бы минимальными.

Задача №6
На предприятии имеется три группы станков, каждая из которых может выполнять пять операций по обработке деталей (операции могут выполняться в любом порядке). Максимальное время работы каждой группы станков равно 100, 250, 180 ч. соответственно. Время выполнения каждой операции составляет 100, 120, 70, 110, 130 ч. соответственно. Производительность каждой группы станков задается матрицей:
Решение: