Методы оптимальных решений

2. Экономическая задача на экстремум
Фирма производит товар двух видов в количестве х и у.
Цены этих товаров равны Р1=110,Р2=70.Функция издержек С(х,у)= 7х2 +8ху+3у2+90. Определить, при каких объемах выпуска достигается максимальная прибыль и найти эту прибыль.
Решение.1) Математическая модель.
Функция прибыли
f(x,y)=110x+70y- (7х2 +8ху+3у2+90). Следует исследовать ее на экстремум.

3. Решение экономической задачи на экстремум
2) z(x,y)=110x+70y- (7х2 +8ху+3у2+90)
1)Частные производные:
zיx=110-14x-8у, zYי=70-8х-6y, zייxx=-14,zייYY =-6,zייxY =-8
2) Найдем стационарные точки функции из условия
откуда, х=5,у=5,т.е.М(5,5,)-стационарная
точка.
3) Проверим ее на экстремум.
D (x, y)=-14×(-6)-(-8)2=20,т.е. экстремум есть. Это максимум.

4. Экономическая задача на условный экстремум
Функция потребления имеет вид u=x y.
Цены товаров x и у соответственно равны
Р1=2 ,Р2=1.
Найти при каких значениях x и у функция u достигает
максимального значения при бюджете равном 200 (а).
Решение. Бюджетное ограничение задается равенством: 2х+у=200. Следовательно, функцию
u=x y требуется исследовать на условный экстремум при условии 2х+у=200 (уравнение связи).

5. Решение экономической задачи на условный экстремум
Выразим из уравнения связи у=200-2х и подставим
в функцию потребления: u=x(200-2x)=200x-2х2 .Это
функция одной переменной х. Найдем ее производную
u′Ꞌ= 200-4x. Стационарная точка функции х=50. Очевидно, что это точка максимума ( ветви параболы направлены вниз). Таким образом, функция потребления достигает максимального значения при
х=50 и у=100 и ее значение . umax =50×100=5000

6. Постановка задачи линейного программирования
Если в экономических задачах оптимизации критерий (целевая функция) и ограничения линейно зависят от параметров, то полученная задача называется задачей линейного программирования (ЗЛП).
К такой задаче, например, относится задача выбора некоторым предприятием номенклатуры и объема продукции, обеспечивающей максимальную прибыль при условии ограниченных ресурсов.

7. Пример задачи линейного программирования
Пусть на предприятии изготавливают два вида продукции Р1 и Р2 используют три вида ресурсов S1 , S2 и S3 ( труд, сырье, оборудование). Известны затраты каждого ресурса на единицу каждой продукции P1: 2,4,2 и Р2 : 3,1,2. Запасы ресурсов
S1 =6; S2 =4; S3 =4. Прибыль от реализации единицы готовой продукции С1 =3 и С2= 6.Требуется найти такие объемы выпуска продукции, при которых прибыль будет максимальна.

8. Математическая модель задачи линейного программирования
Обозначим объемы выпуска продукции х1 и х2, тогда прибыль L(x1 ,x2 )= 3x1+6x2 (1) должна быть максимальна и выполнялись бы ограничения, соответствующие ограничениям на запасы ресурсов:
2х1+3х2 ≤6
4x1+x2 ≤ 4 (2)
2x1+2x2 ≤ 4
объемы выпуска х1≥0 и x2 ≥0

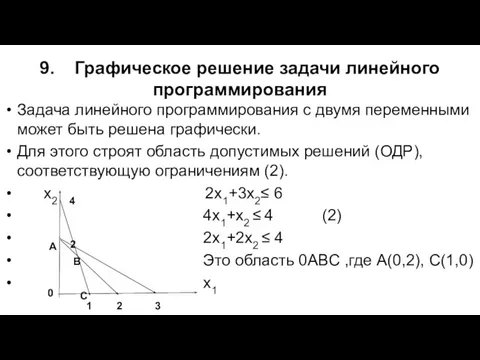
9. Графическое решение задачи линейного программирования
Задача линейного программирования с двумя переменными может быть решена графически.
Для этого строят область допустимых решений (ОДР), соответствующую ограничениям (2).
x2 2х1+3х2≤ 6
4x1+x2 ≤ 4 (2)
2x1+2x2 ≤ 4
Это область 0АВС ,где А(0,2), С(1,0)
х1
4
2
2
3
1
0
В
А
С