Содержание
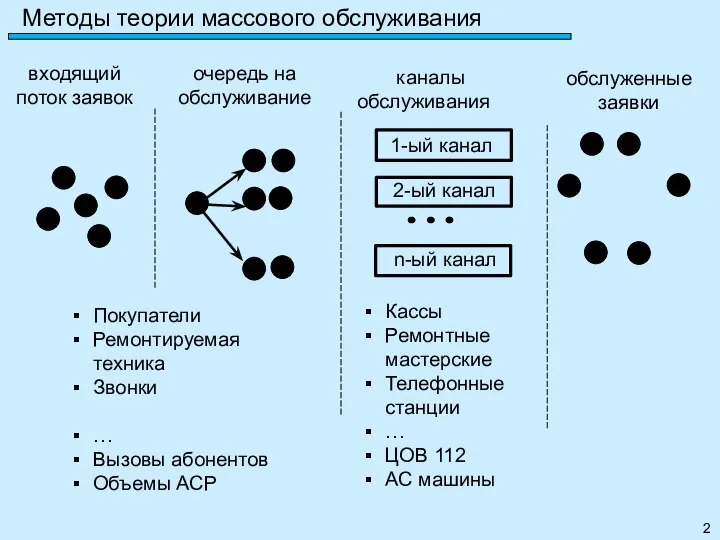
- 2. каналы обслуживания 1-ый канал 2-ый канал n-ый канал входящий поток заявок обслуженные заявки Кассы Ремонтные мастерские
- 3. Методы теории массового обслуживания Предмет теории массового обслуживания - установление зависимости между характером потока заявок, числом
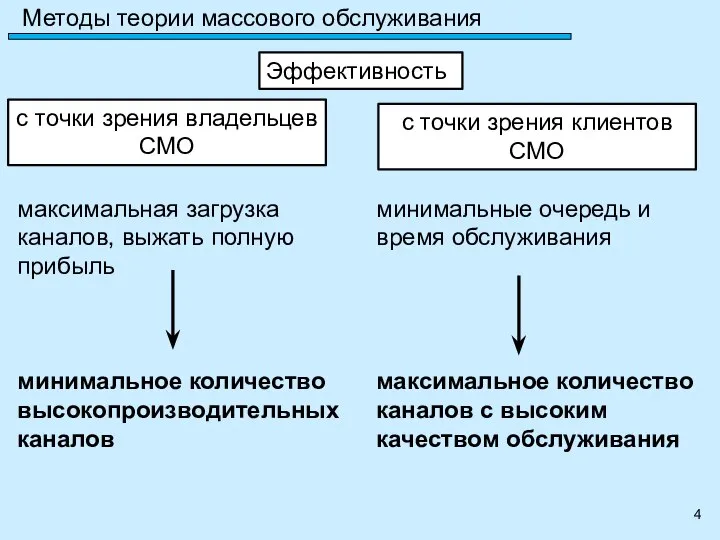
- 4. Эффективность с точки зрения владельцев СМО с точки зрения клиентов СМО максимальная загрузка каналов, выжать полную
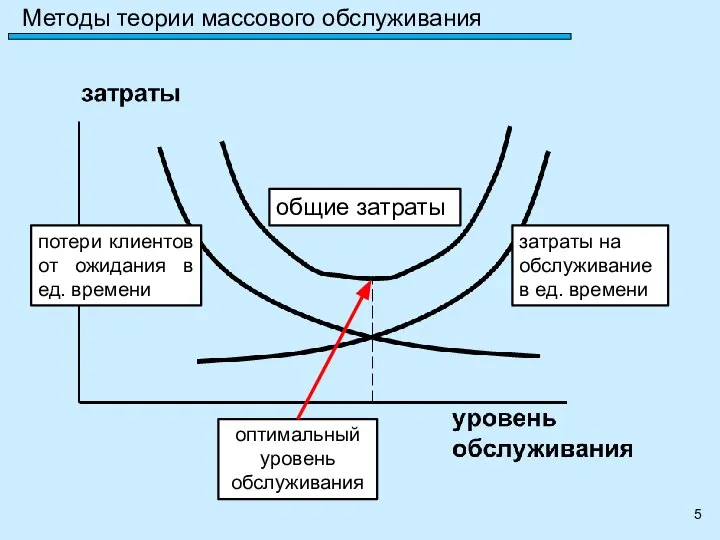
- 5. Методы теории массового обслуживания потери клиентов от ожидания в ед. времени затраты на обслуживание в ед.
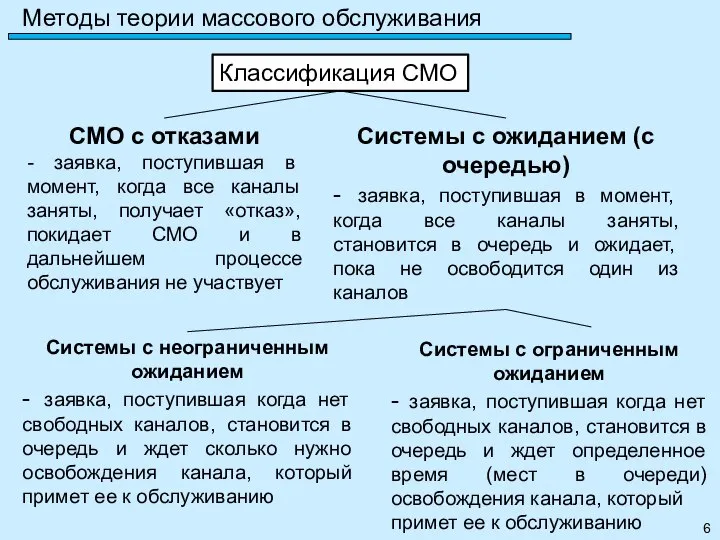
- 6. Методы теории массового обслуживания Классификация СМО Системы с ожиданием (с очередью) - заявка, поступившая в момент,
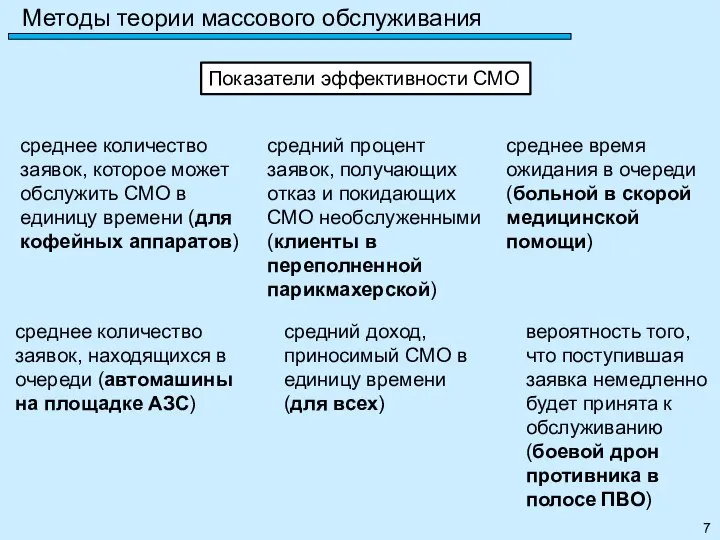
- 7. Методы теории массового обслуживания среднее количество заявок, которое может обслужить СМО в единицу времени (для кофейных
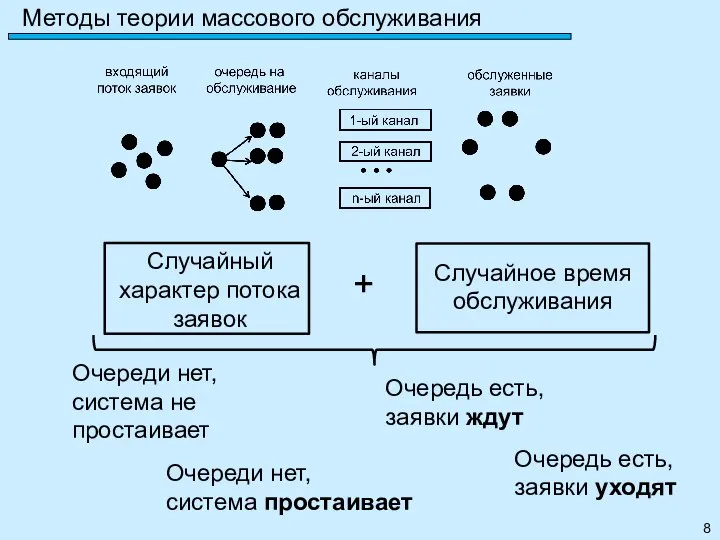
- 8. Случайное время обслуживания Методы теории массового обслуживания Очереди нет, система не простаивает Очереди нет, система простаивает
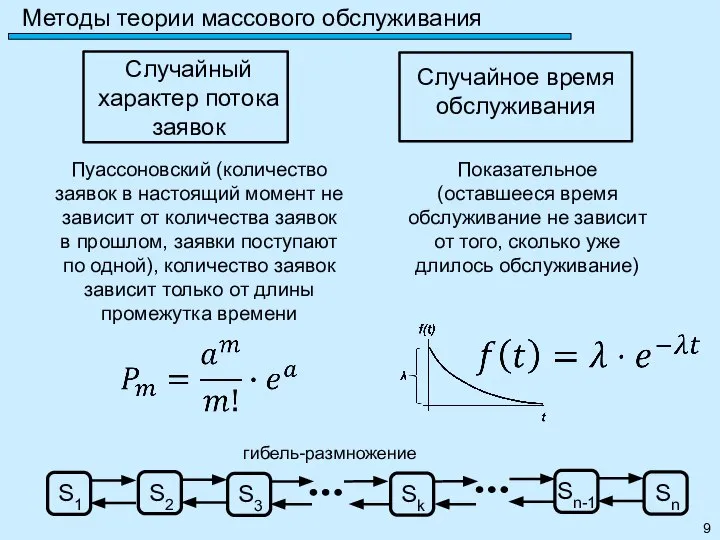
- 9. Методы теории массового обслуживания Случайное время обслуживания Пуассоновский (количество заявок в настоящий момент не зависит от
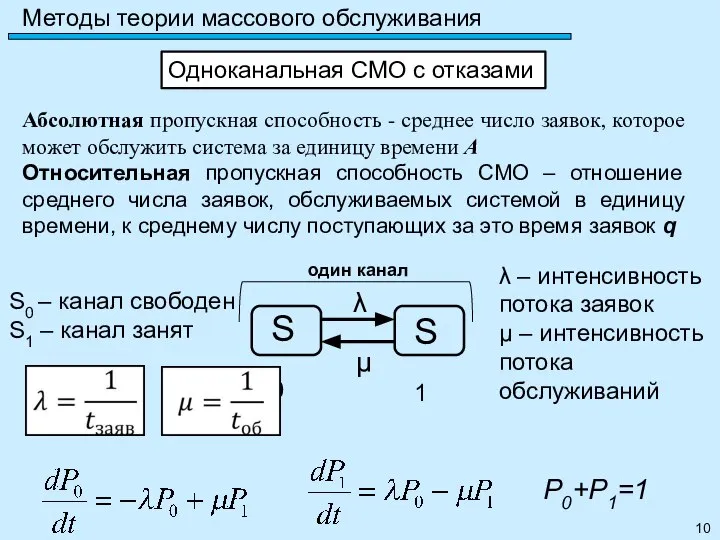
- 10. Методы теории массового обслуживания Одноканальная СМО с отказами P0+P1=1 Абсолютная пропускная способность - среднее число заявок,
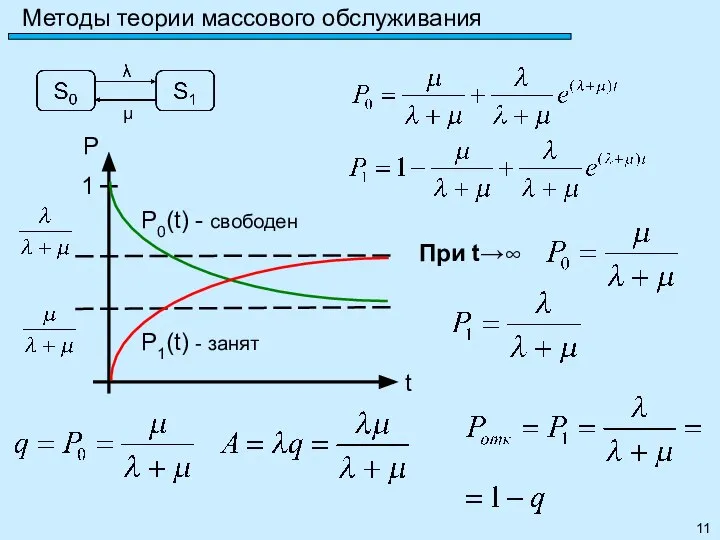
- 11. Методы теории массового обслуживания При t→∞
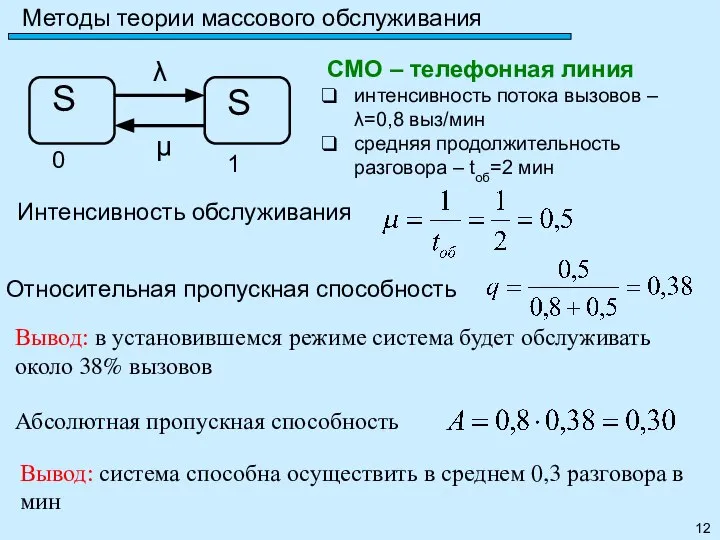
- 12. Методы теории массового обслуживания СМО – телефонная линия интенсивность потока вызовов – λ=0,8 выз/мин средняя продолжительность
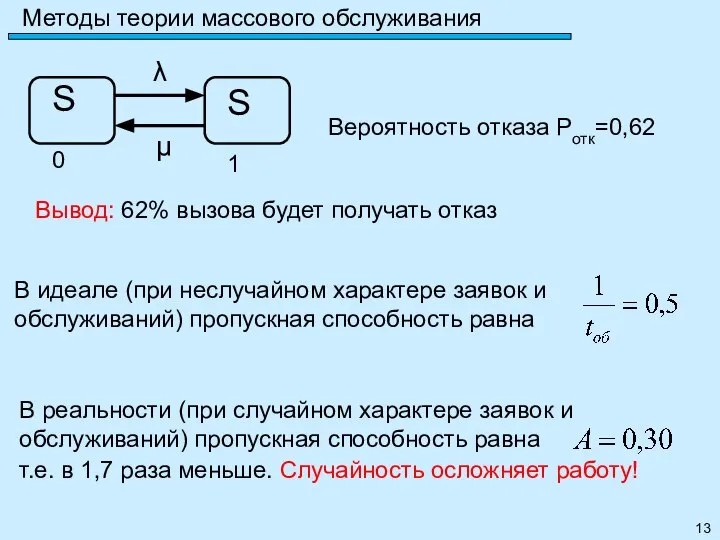
- 13. Методы теории массового обслуживания Вывод: 62% вызова будет получать отказ Вероятность отказа Pотк=0,62 В идеале (при
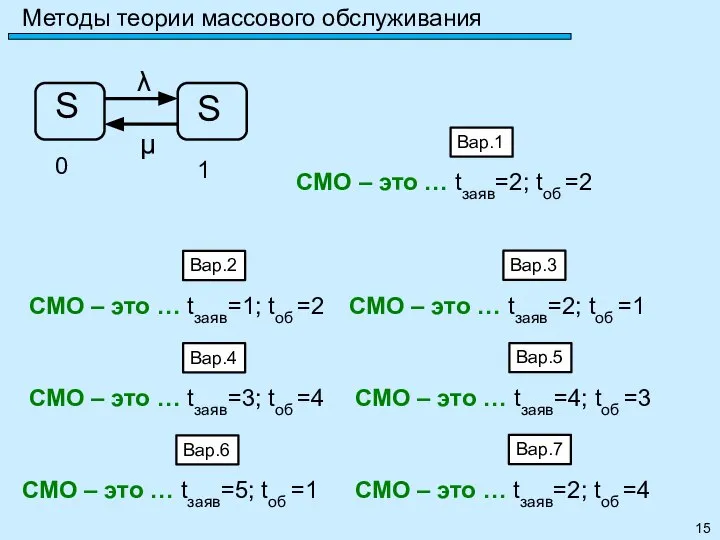
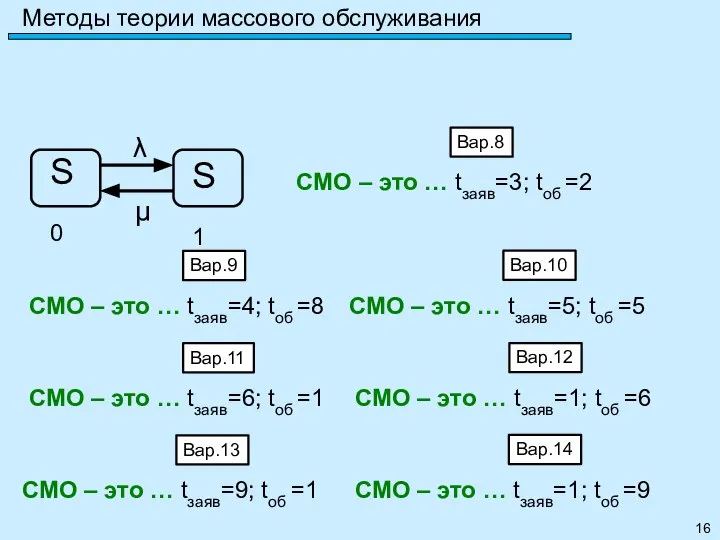
- 14. Метод марковских случайных процессов Задание 22: Привести пример одноканальной СМО с отказами и рассчитать её параметры:
- 15. Методы теории массового обслуживания
- 16. Методы теории массового обслуживания
- 17. Методы теории массового обслуживания
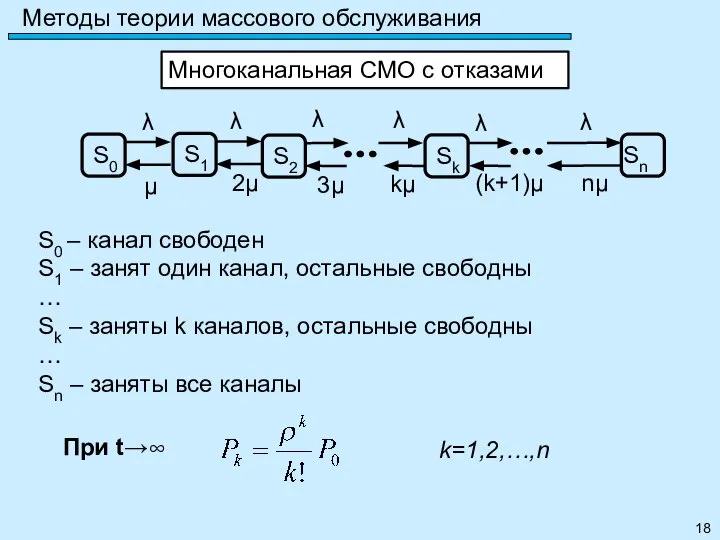
- 18. Методы теории массового обслуживания Многоканальная СМО с отказами S0 – канал свободен S1 – занят один
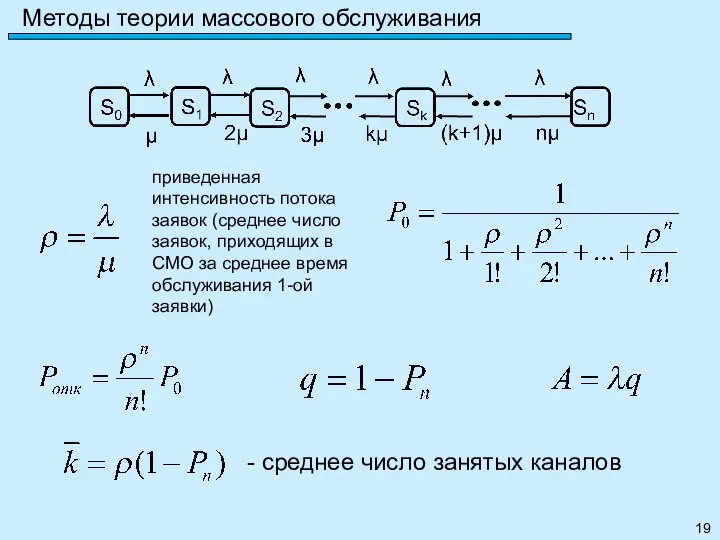
- 19. Методы теории массового обслуживания - среднее число занятых каналов приведенная интенсивность потока заявок (среднее число заявок,
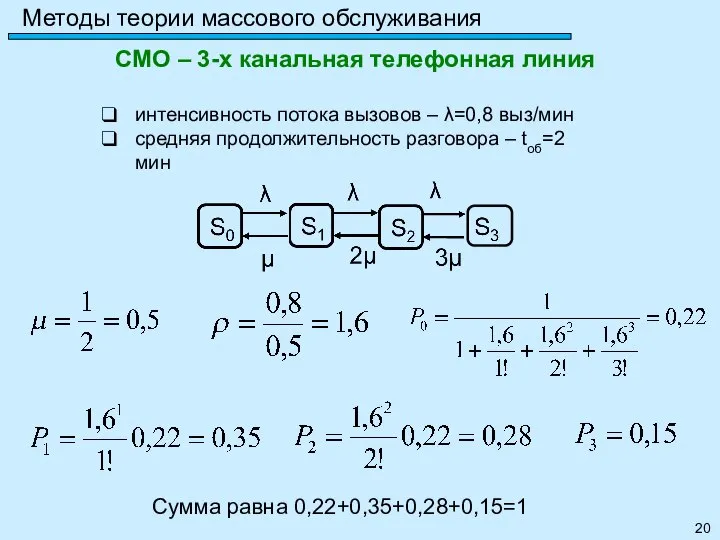
- 20. Методы теории массового обслуживания СМО – 3-х канальная телефонная линия интенсивность потока вызовов – λ=0,8 выз/мин
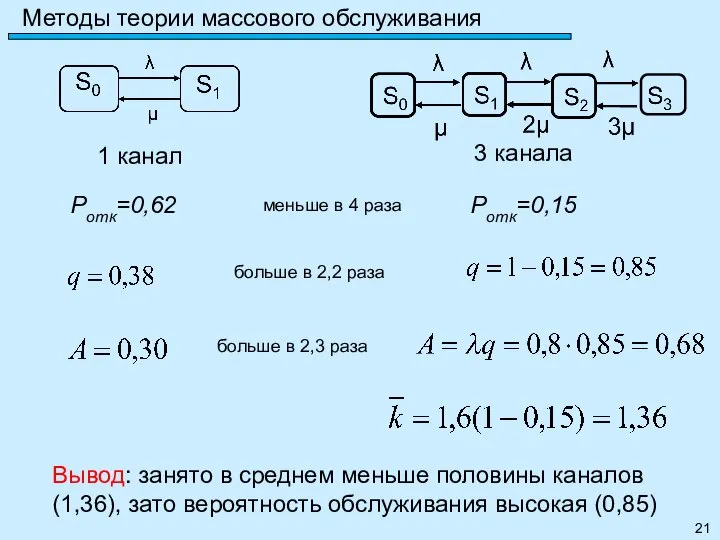
- 21. Методы теории массового обслуживания Pотк=0,62 Pотк=0,15 меньше в 4 раза больше в 2,2 раза больше в
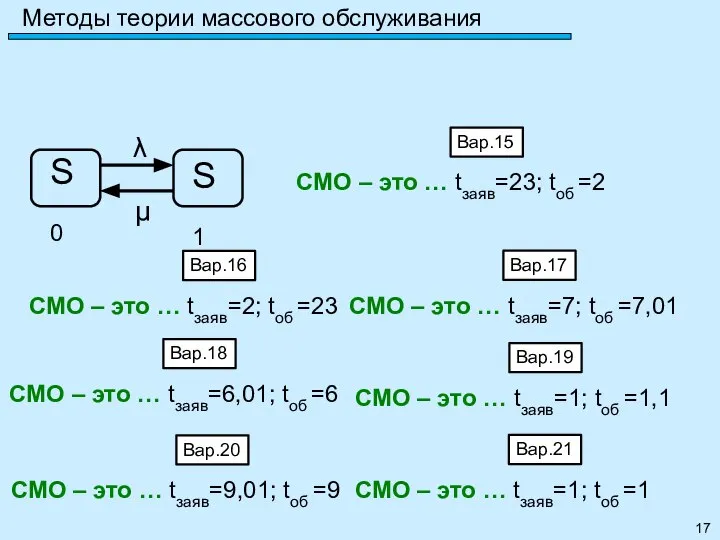
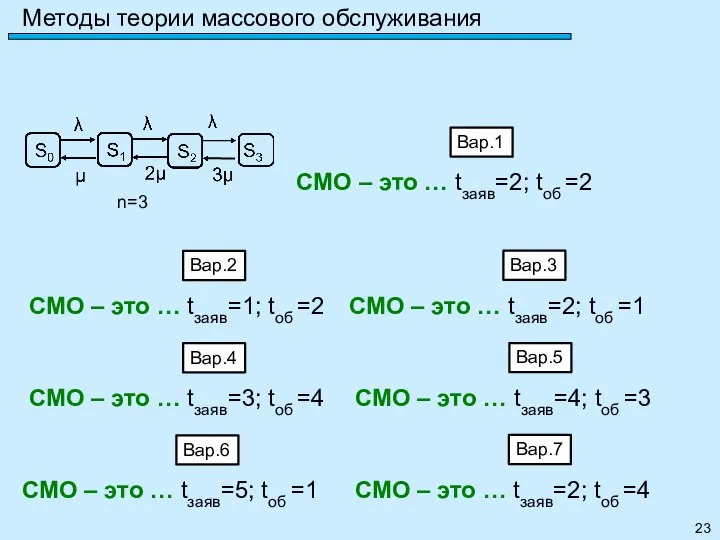
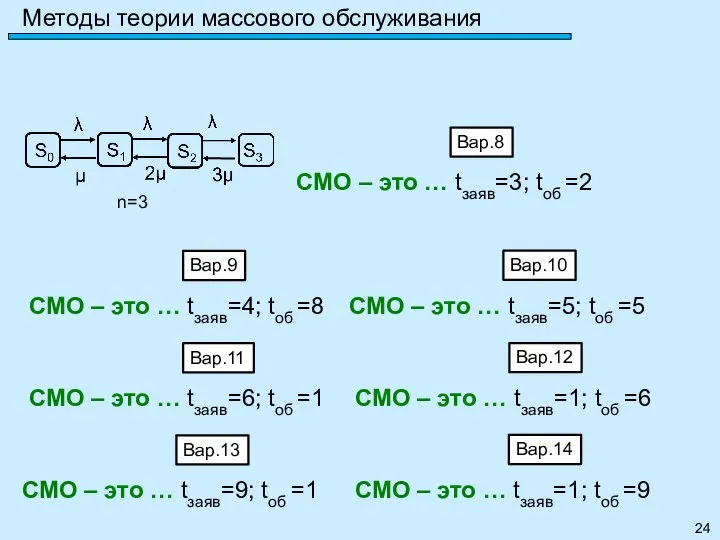
- 22. Метод марковских случайных процессов Задание 23: Привести пример многоканальной СМО с отказами и рассчитать её параметры:
- 23. Методы теории массового обслуживания
- 24. Методы теории массового обслуживания
- 25. Методы теории массового обслуживания
- 26. Методы теории массового обслуживания Одноканальная СМО с ожиданием, очередь ограничена m заявками очереди нет S0 –
- 27. Методы теории массового обслуживания среднее число заявок, находящихся в очереди среднее число заявок, связанных с системой
- 28. Методы теории массового обслуживания среднее время ожидания заявки в очереди среднеe время пребывания заявки в системе
- 29. Методы теории массового обслуживания
- 30. Метод марковских случайных процессов Задание 24: Привести пример одноканальной СМО с ожиданиями и рассчитать её параметры:
- 31. Методы теории массового обслуживания
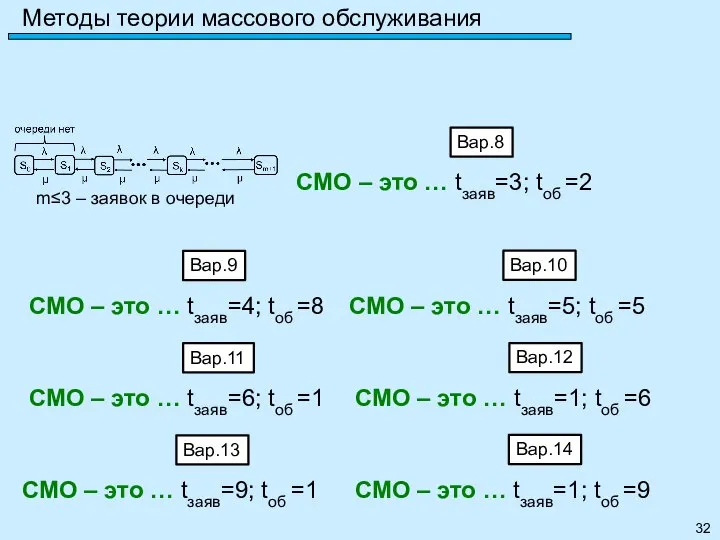
- 32. Методы теории массового обслуживания
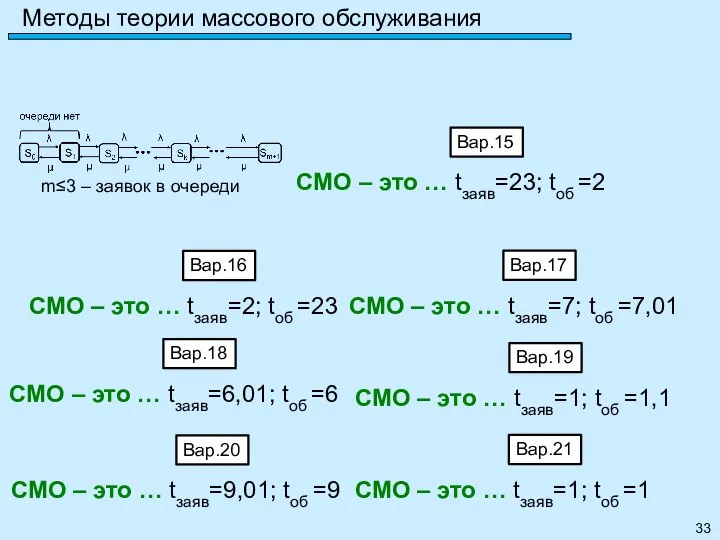
- 33. Методы теории массового обслуживания
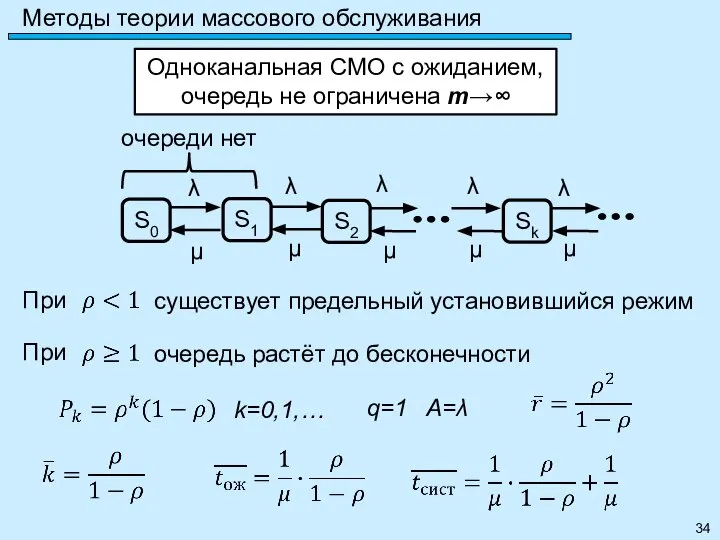
- 34. Методы теории массового обслуживания Одноканальная СМО с ожиданием, очередь не ограничена m→∞ k=0,1,… q=1 A=λ
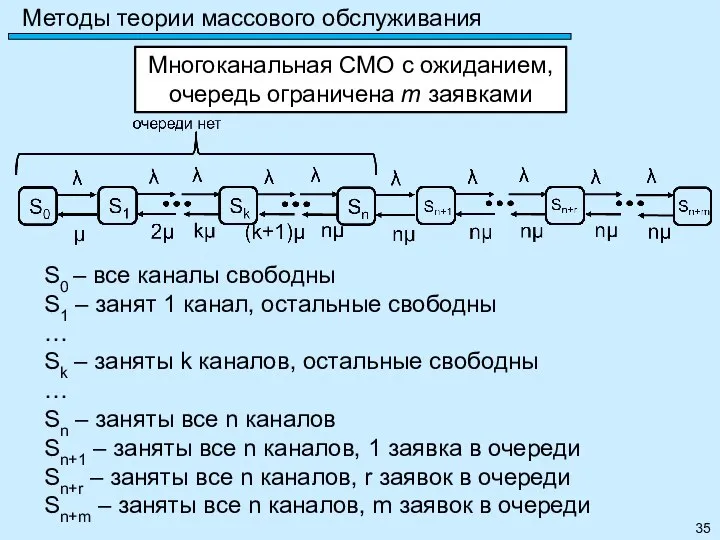
- 35. Методы теории массового обслуживания Многоканальная СМО с ожиданием, очередь ограничена m заявками S0 – все каналы
- 36. Методы теории массового обслуживания …
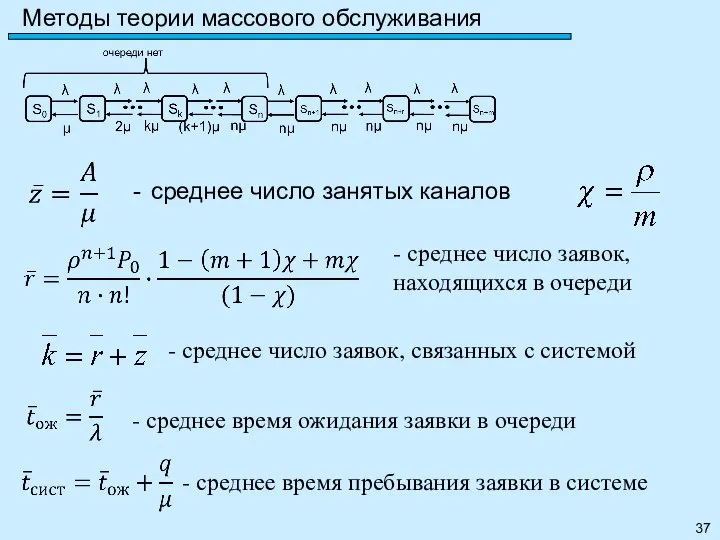
- 37. Методы теории массового обслуживания среднее число занятых каналов - среднее число заявок, находящихся в очереди -
- 38. Методы теории массового обслуживания АЗС - СМО с двумя каналами обслуживания (двумя колонками): площадка при станции
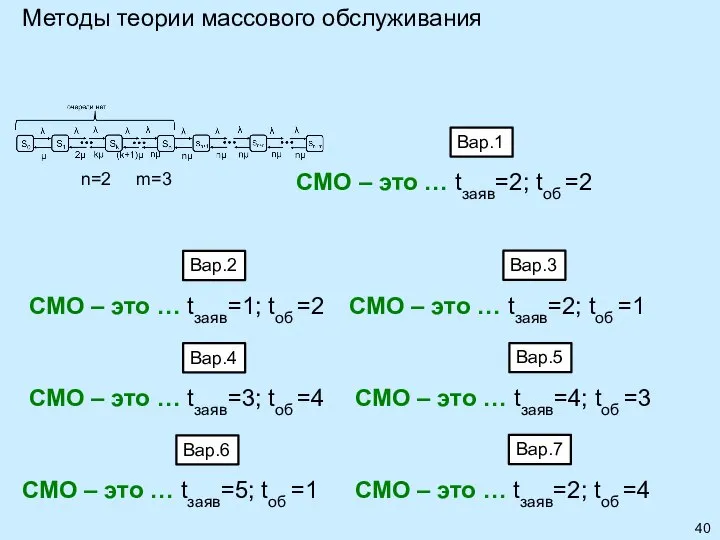
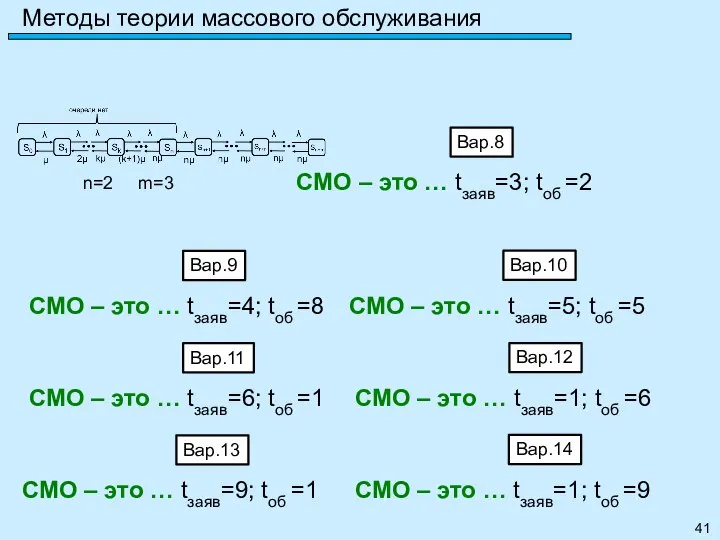
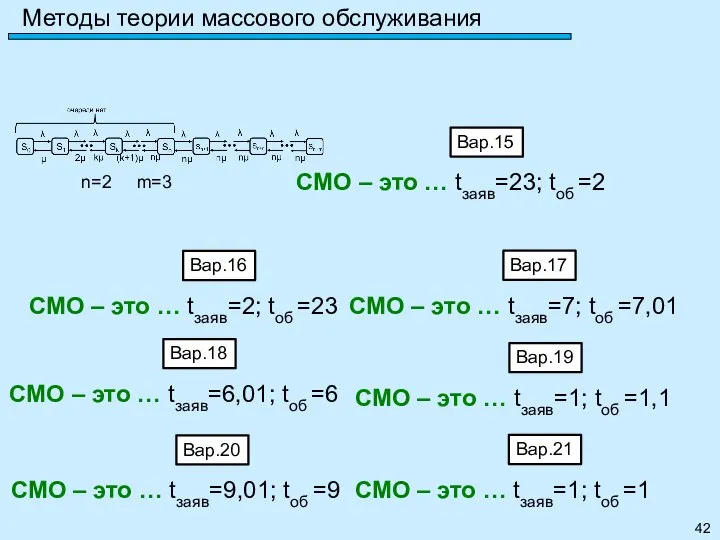
- 39. Метод марковских случайных процессов Задание 25: Привести пример мноканальной СМО с ожиданиями и рассчитать её параметры:
- 40. Методы теории массового обслуживания
- 41. Методы теории массового обслуживания
- 42. Методы теории массового обслуживания
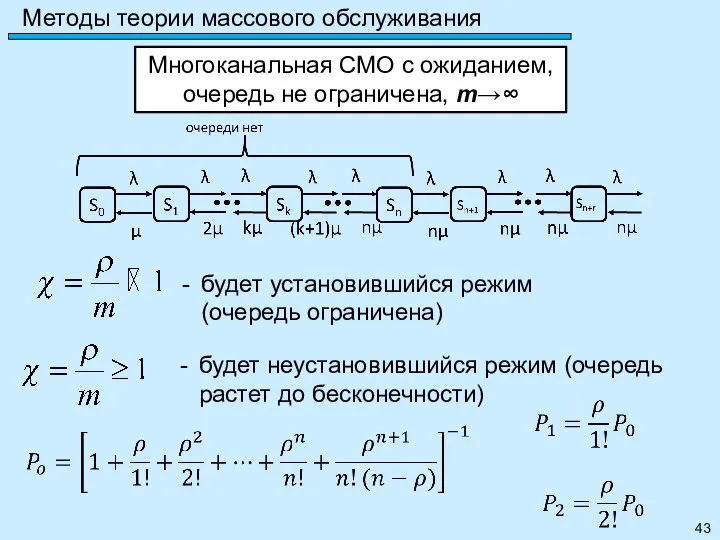
- 43. Методы теории массового обслуживания Многоканальная СМО с ожиданием, очередь не ограничена, m→∞ будет установившийся режим (очередь
- 44. Методы теории массового обслуживания Каждая заявка рано или поздно будет обслужена, поэтому:
- 45. Методы теории массового обслуживания АЗС - СМО с двумя каналами обслуживания (двумя колонками): других АЗС в
- 46. Метод марковских случайных процессов Задание 26: Привести пример мноканальной СМО с ожиданиями и рассчитать её параметры:
- 47. Методы теории массового обслуживания
- 48. Методы теории массового обслуживания
- 49. Методы теории массового обслуживания
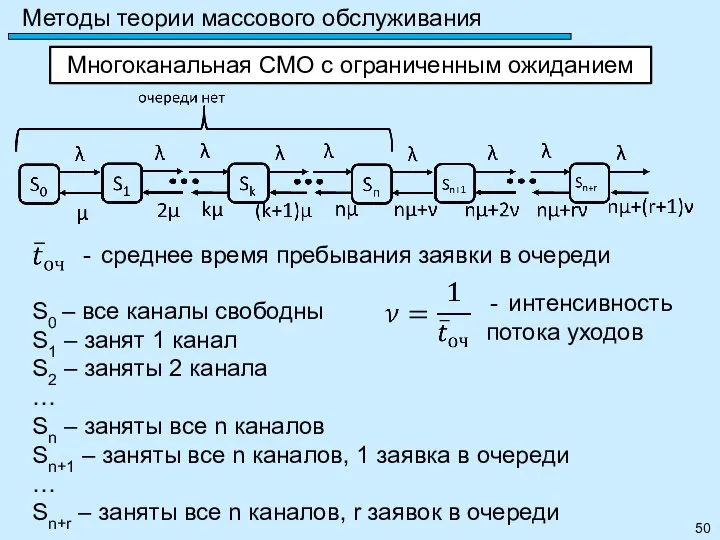
- 50. Методы теории массового обслуживания Многоканальная СМО с ограниченным ожиданием S0 – все каналы свободны S1 –
- 51. Методы теории массового обслуживания Многоканальная СМО с ограниченным ожиданием достаточно до r Pотк не имеет смысла
- 52. Дано: статистика ДТП на территории субъекта РФ производительность АС вертолетов по ведению АСР при ДТП Найти:
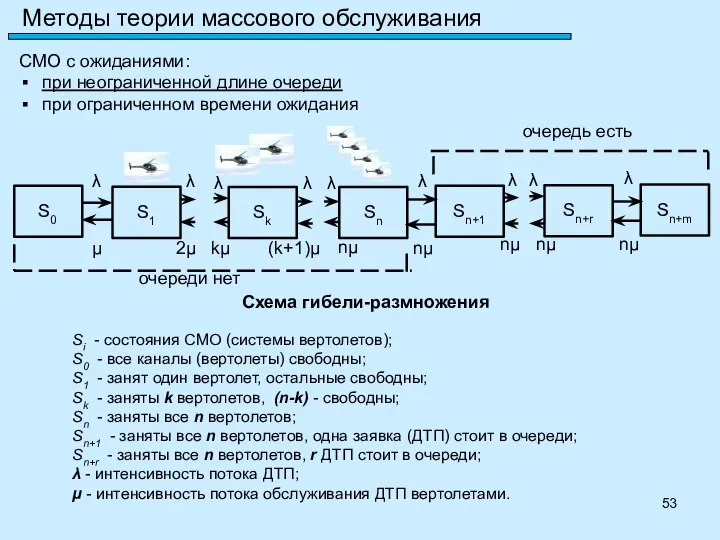
- 53. Si - состояния СМО (системы вертолетов); S0 - все каналы (вертолеты) свободны; S1 - занят один
- 54. Интенсивность потока заявок Интенсивность потока обслуживания Среднее время ожидания пострадавшими в ДТП спасателей и медицинских работников
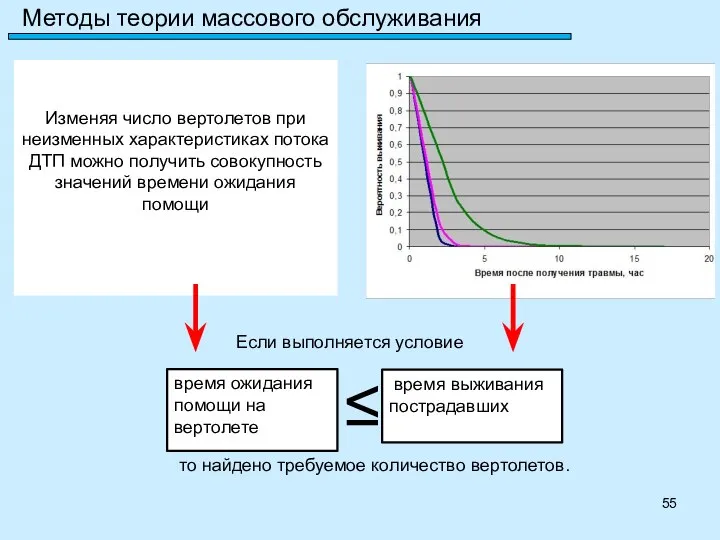
- 55. Изменяя число вертолетов при неизменных характеристиках потока ДТП можно получить совокупность значений времени ожидания помощи Методы
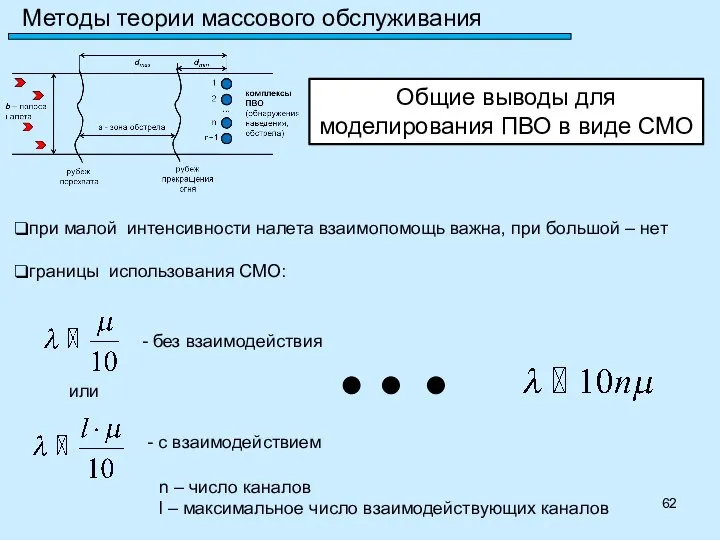
- 56. Методы теории массового обслуживания Пример СМО: система противовоздушной обороны от дронов: количество средств ПВО – n
- 57. Методы теории массового обслуживания Пример СМО с отказами и полной взаимопомощью между каналами: система противовоздушной обороны
- 58. Методы теории массового обслуживания Пример СМО с отказами, взаимопомощью и отсутствием информации о результатах обслуживания: система
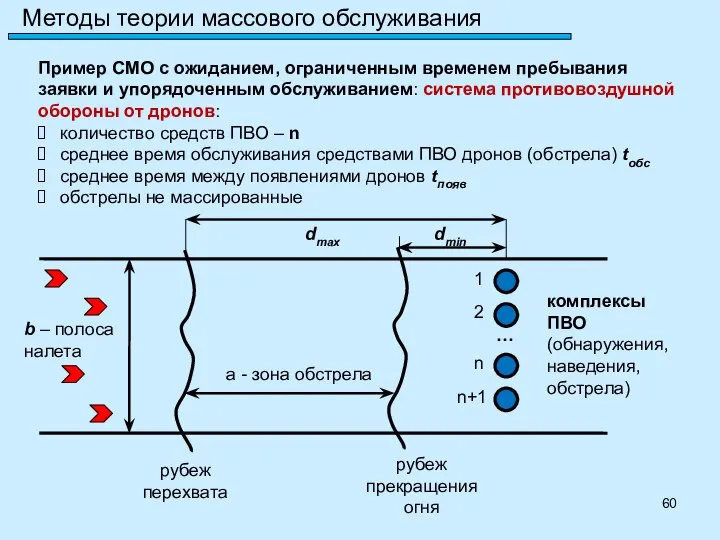
- 59. Методы теории массового обслуживания Пример СМО с ожиданием, ограниченным временем пребывания заявки и упорядоченным обслуживанием: система
- 60. Методы теории массового обслуживания Пример СМО с ожиданием, ограниченным временем пребывания заявки и упорядоченным обслуживанием: система
- 61. Методы теории массового обслуживания μ – эффективная скорострельность одного комплекса g – количество установок, связанных с
- 62. Методы теории массового обслуживания Общие выводы для моделирования ПВО в виде СМО при малой интенсивности налета
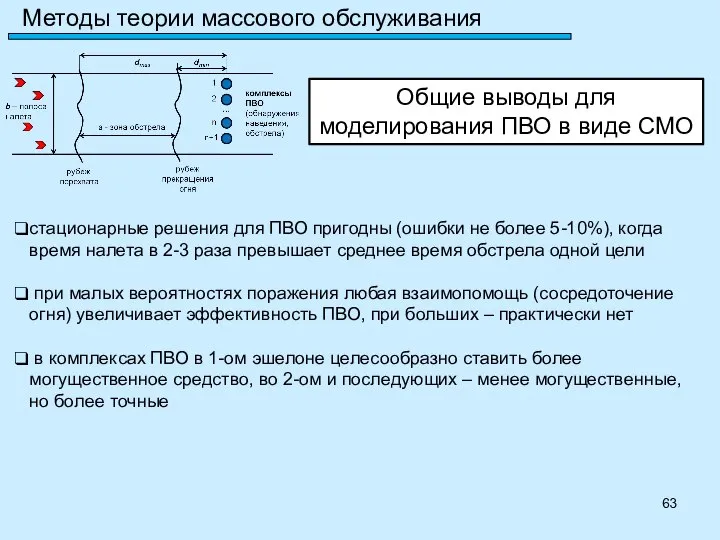
- 63. Методы теории массового обслуживания Общие выводы для моделирования ПВО в виде СМО стационарные решения для ПВО
- 65. Скачать презентацию




















 Коронавирус (COVID-19). Чек-лист для работников АО Группа Илим при выезде в отпуск или в командировку
Коронавирус (COVID-19). Чек-лист для работников АО Группа Илим при выезде в отпуск или в командировку ПРЕДУПРЕДИТЬ – ЗНАЧИТ СПАСТИ
ПРЕДУПРЕДИТЬ – ЗНАЧИТ СПАСТИ Расшифровав надпись, вы отгадаете тему урока.
Расшифровав надпись, вы отгадаете тему урока. Описание картины Петра Кончаловского «Сирень в корзине»
Описание картины Петра Кончаловского «Сирень в корзине» Река Которосль – малая река Нечерноземья
Река Которосль – малая река Нечерноземья Морской порт Санкт-Петербург. Отчет по результатам обхода. 1 и 2 районы порта
Морской порт Санкт-Петербург. Отчет по результатам обхода. 1 и 2 районы порта Модульное обучение
Модульное обучение Додавання малюнківіз файлу до текстового документа
Додавання малюнківіз файлу до текстового документа Система оценки достижений планируемых результатов освоения основной образовательной программы начального общего образования. П
Система оценки достижений планируемых результатов освоения основной образовательной программы начального общего образования. П Речевая деятельность
Речевая деятельность Центр дополнительного образования г. Холма 2020-2021 учебный год
Центр дополнительного образования г. Холма 2020-2021 учебный год Азия и Африка в современном мире
Азия и Африка в современном мире 20140311_proverochnaya_rabota_po_teme_klimat_rossii
20140311_proverochnaya_rabota_po_teme_klimat_rossii Кому мы нужны в Америке
Кому мы нужны в Америке Бизнес-центр «Айсберг»
Бизнес-центр «Айсберг» ТЕМА 10. ЕСКК ТЭСИ РФ
ТЕМА 10. ЕСКК ТЭСИ РФ Яхт-клуб Аврора. Яхт-клуб Пеликан
Яхт-клуб Аврора. Яхт-клуб Пеликан Индивидуальный подход к учащимся в процессе обучения биологии в профильных группах
Индивидуальный подход к учащимся в процессе обучения биологии в профильных группах Геополитика (географическая политика)
Геополитика (географическая политика) Какие газеты и журналы пришли в нашу жизнь
Какие газеты и журналы пришли в нашу жизнь Планирование спортивно-массового мероприятия
Планирование спортивно-массового мероприятия Проектирование локальной вычислительной сети предприятия ООО СпецГидрострой
Проектирование локальной вычислительной сети предприятия ООО СпецГидрострой Требования безопасности к техническому состоянию автотранспорта
Требования безопасности к техническому состоянию автотранспорта  Сталинградская битва (9 класса)
Сталинградская битва (9 класса) Слово 1 класс
Слово 1 класс Горнодобывающая промышленность и металлургия
Горнодобывающая промышленность и металлургия Жизнь Ломоносова -
Жизнь Ломоносова - Школьная форма : её особенности, значение и важность
Школьная форма : её особенности, значение и важность