Михайлова Татьяна Анатольевна учитель математики школы № 60 г. Оби Новосибирской области

Тема урока: Тетраэдр и построение сечений
Цель: выработать навыки решения задач
на построение сечений тетраэдра, развитие познавательного интереса, воспитание ответственного отношения к учебному труду
Оборудование: персональный компьютер, проектор; используется программа «Живая геометрия», Microsoft Power Point

Применение персональных компьютеров на уроке геометрии
1.Возможность продемонстрировать сечения тетраэдра с разных сторон
2.Показать изменения площади сечений
3.Осуществляется быстрый контроль со стороны учителя

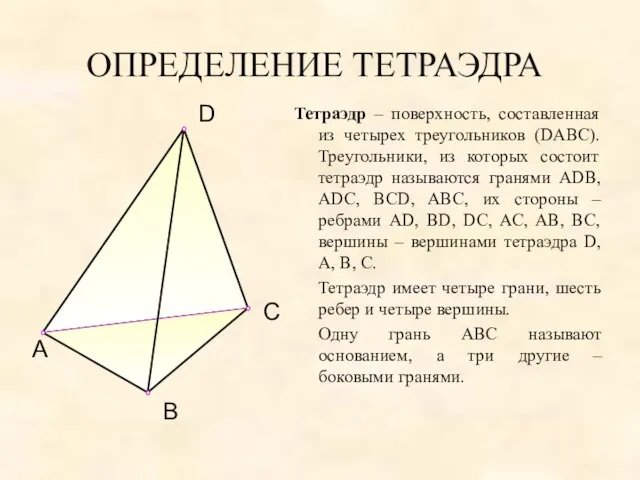
ОПРЕДЕЛЕНИЕ ТЕТРАЭДРА
Тетраэдр – поверхность, составленная из четырех треугольников (DABC). Треугольники, из которых состоит тетраэдр называются гранями ADB, ADC, BCD, ABC, их стороны – ребрами AD, BD, DC, AC, AB, BC, вершины – вершинами тетраэдра D, A, B, C.
Тетраэдр имеет четыре грани, шесть ребер и четыре вершины.
Одну грань ABC называют основанием, а три другие – боковыми гранями.

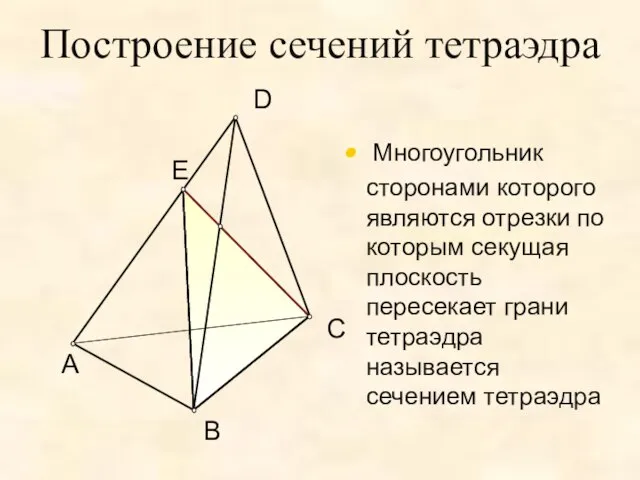
Построение сечений тетраэдра
Многоугольник
сторонами которого являются отрезки по которым секущая плоскость пересекает грани тетраэдра называется сечением тетраэдра

Задачи на построение сечений тетраэдра
Задача 1
На рёбрах АВ, ВD и СD тетраэдра АВСД отмечены точки М, N, Р. Построить сечение тетраэдра плоскостью МNР.
Решение.
1.Построим прямую МЕ, по которой пересекаются плоскости МNР и АВС.
2. Точка М является их общей точкой.
3. Продолжим отрезки NР и ВС до их пересечения в точке Е.
4.Прямая МЕ пересекает ребро АС в точке Т.
5.Четырёхугольник МNРТ- искомое сечение.

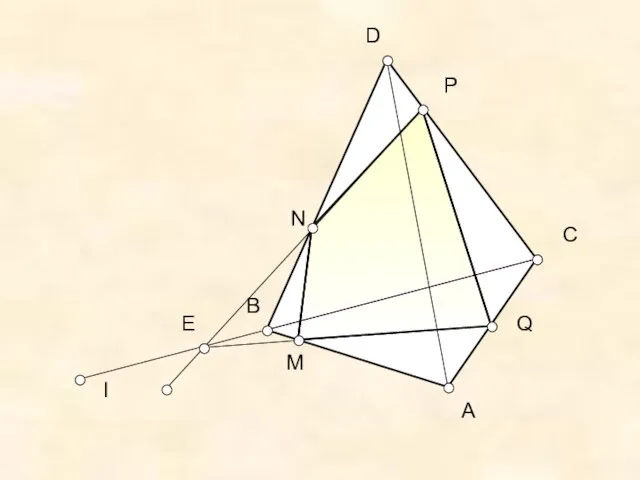
Задача 2
Если прямые NP и ВС параллельны, то прямая NP параллельна грани АВС, поэтому плоскость MNP пересекает эту грань по прямой МЕ, параллельно прямой NP. Точка Q, как и в первой задаче, есть точка пересечения ребра АС с прямой МЕ.

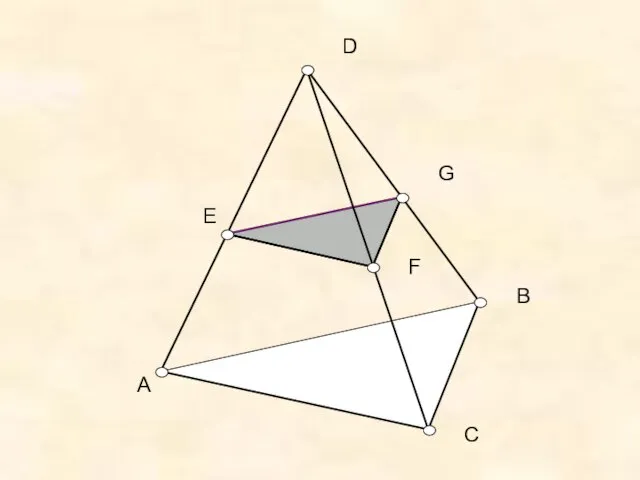
Задача 3
Решение
1. Проведем через точку М прямую параллельную отрезку АВ, и обозначим буквами P и Q точки пересечения этой прямой с боковыми ребрами DA и DB.
2. Через точку Р проведем прямую, параллельную отрезку АС, и обозначим буквой R точку пересечения этой прямой с ребром DC
3. Треугольник PQR – искомое сечение.
Точка М лежит на боковой грани ADB тетраэдра DABC. Построить сечение тетраэдра плоскостью, проходящей через точку М параллельно основанию АВС.

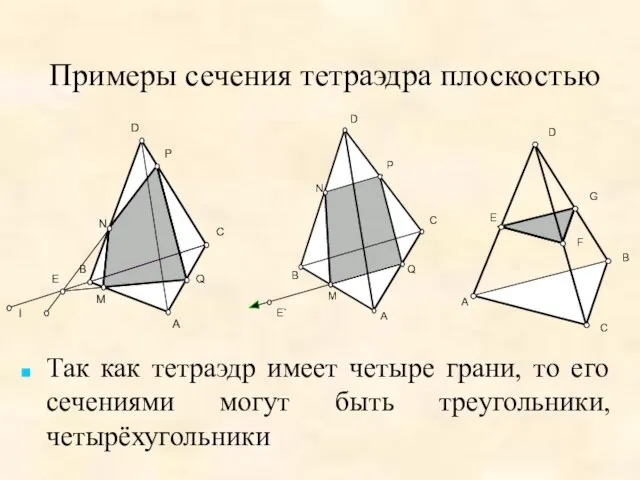
Примеры сечения тетраэдра плоскостью
Так как тетраэдр имеет четыре грани, то его сечениями могут быть треугольники, четырёхугольники

Используемое программное обеспечение
Позволяет создавать красочные, варьируемые и редактируемые чертежи, осуществлять операции над ними, а также производить все необходимые измерения.
Программа «Живая Геометрия» является электронным аналогом готовальни с дополнительными динамическими возможностями и со стандартными компьютерными функциями типа редактирования, каталогизирования и т.п.