Слайд 2Подмножество
Множество К называется подмножеством множества А, если любой элемент множества К принадлежит
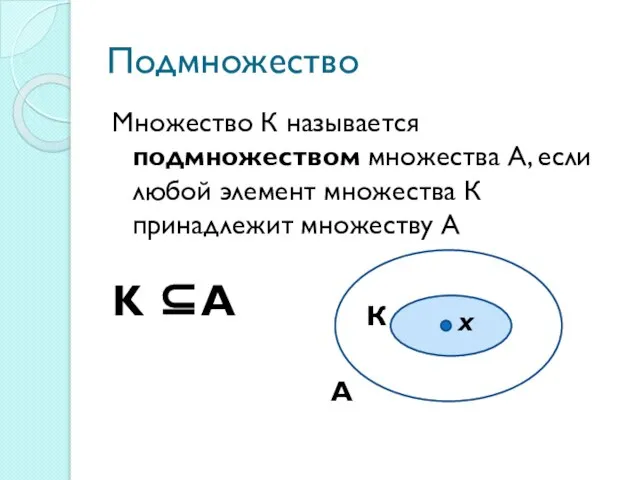
Слайд 3Подмножество
Множество К называется подмножеством множества А, если любой элемент множества К принадлежит

множеству А
∀х∈ К ⇒ х∈ А
Слайд 4Кванторы
Специальные математические символы, облегчающие запись математических выражений
Георг Кантор
Кантор придумал кванторы

Слайд 5Кванторы
∀ − квантор всеобщности
«для любого»
All (англ)

Слайд 6Кванторы
∃ − квантор существования
«существует»
Exist (англ)

Слайд 7Универсальное множество
Множество , которому принадлежат все элементы, обладающие данным характеристическим свойством
Универсальное множество

своё для каждой задачи
Слайд 8Равные множества
Множества, состоящие из одинаковых элементов
А = {1, 2, 4, 8, 16}
B

= {20, 21, 22, 23, 24}
C = {x : x= 2n, n = 0, 1, 2, 3, 4}
A = B = C
Слайд 9Равные множества
Если A = B , то
A⊆ B и B ⊆A

Слайд 10Задача
На множестве U всех букв русского алфавита заданы множества
А = {ё, к,

л, м,н} В ={к, о, з, ё, л}
С = {б, ы, ч, о, к}
Найдите следующие множества и изобразите их кругами Эйлера
1) AUB 2) A∩B 3) (A∩B)UC
4) (AUC)∩B 5) U\(AUB UС)
Слайд 11Задача
Даны числовые промежутки
А= [-4; 5], В =(2; 6), С = (5, 10]
Найдите
![Задача Даны числовые промежутки А= [-4; 5], В =(2; 6), С =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/367634/slide-10.jpg)
следующие множества и изобразите их на числовой прямой и кругами Эйлера
1) AUB 2) A∩B 3) (СUB)\(A∩B)
4) (A∩B)UC 5) (AUB)\ (A∩B)
Слайд 12Формула мощности объединения множеств

Слайд 13Задача 1
В Асбестовском филиале Уральского промышленно-экономического техникума 2 группы юристов.
В группе азПСОу-108

учится 11 человек.
В группе азПСОу-304 – 9 человек.
Сколько всего студентов-юристов в Асбестовском филиале?
Слайд 14Обозначения
А – множество студентов группы азПСОу-108
|А|=11
В – множество студентов группы азПСОу-304

|В|=9
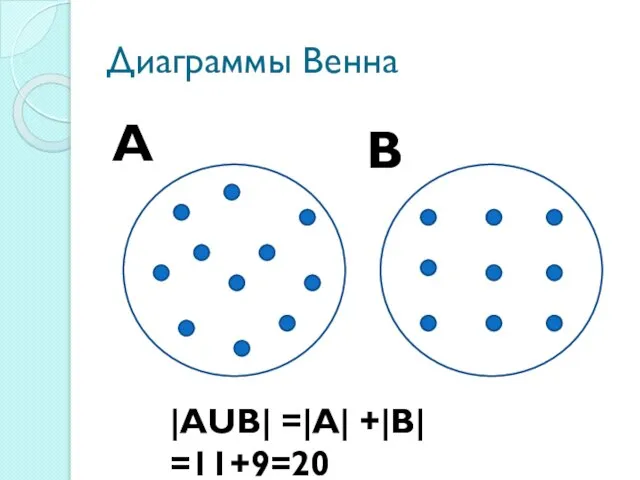
Слайд 15Диаграммы Венна
А
В
|АUВ| =|А| +|В| =11+9=20
Слайд 16Задача 2
Все студенты группы азПСОу-108 очень любят заниматься рукоделием. При этом они

предпочитают только 2 вида рукоделия: плетение из бисера и вышивку крестиком.
1. 7 человек плетут фенечки из бисера.
2. 6 студентов занимаются вышивкой крестиком.
3. 2 человека занимаются обоими видами рукоделия.
Сколько студентов в группе азПСОу-108?
Слайд 17Обозначения
А – множество студентов группы азПСОу-108, увлекающихся бисероплетением
|А|=7
В – множество студентов

группы азПСОу-108, вышивающих крестиком
|В|=6
Слайд 18Обозначения
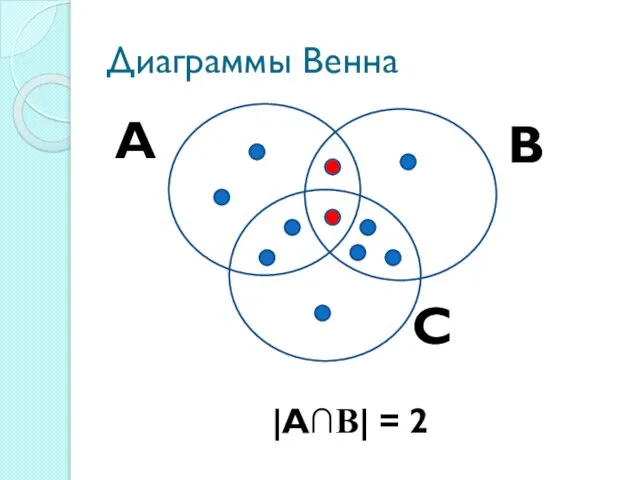
А∩В – множество студентов группы азПСОу-108, увлекающихся бисероплетением и вышивкой одновременно
|А∩В|=2

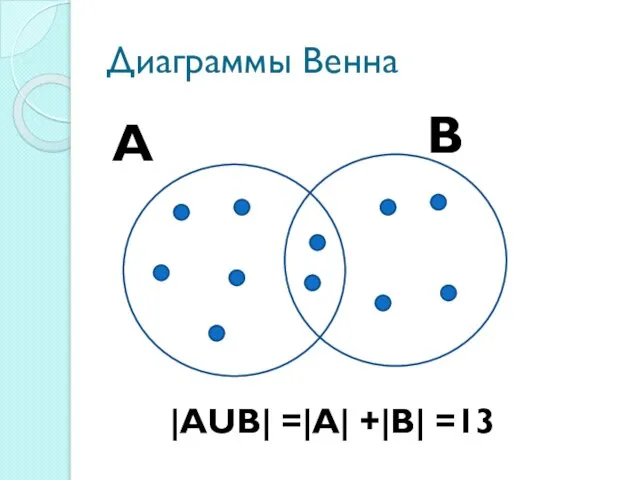
Слайд 19Диаграммы Венна
А
В
|АUВ| =|А| +|В| =13
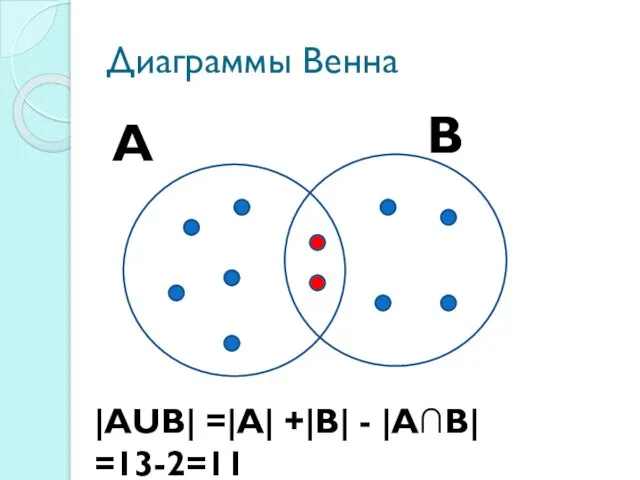
Слайд 20Диаграммы Венна
А
В
|АUВ| =|А| +|В| - |А∩В| =13-2=11
Слайд 21Формула мощности объединения двух множеств
|АUВ| =|А| +|В| - |А∩В|

Слайд 22ФОРМУЛА МОЩНОСТИ ОБЪЕДИНЕНИЯ ТРЁХ МНОЖЕСТВ

Слайд 23Задача 3
Все студенты группы азПСОу-108 очень любят заниматься спортом.
При этом они

предпочитают только 3 вида спорта: синхронное плавание, кёрлинг и спортивное перетягивание каната.
Сколько студентов в этой талантливой группе, если:
Слайд 24Задача 3
1. 6 человек плавают синхронно.
2. 6 студентов занимаются кёрлингом.
3. 7

человек перетягивают канат.
4. Двое кёрлингистов также занимаются синхронным плаванием.
5. Перетягивать канат любят четыре человека из команды кёрлингистов.
6. Синхронным плаванием и перетягиванием каната одновременно увлекаются 3 человека.
7. Всеми тремя видами спорта занимается только 1 студент
Слайд 25Обозначения
А – множество студентов азПСОу-108, занимающихся в секции синхронного плавания
|А|=6
В –

множество студентов-кёрлингистов группы азПСОу-108
|В|=6
С – множество студентов группы азПСОу-108, любящих перетягивать канат
|С|=7
Слайд 26Обозначения
А∩B – множество студентов азПСОу-108, занимающихся синхронным плаванием и кёрлингом одновременно
|А∩B|=2
В∩C

– множество студентов-кёрлингистов группы азПСОу-108, любящих перетягивать канат
|В∩С|=4
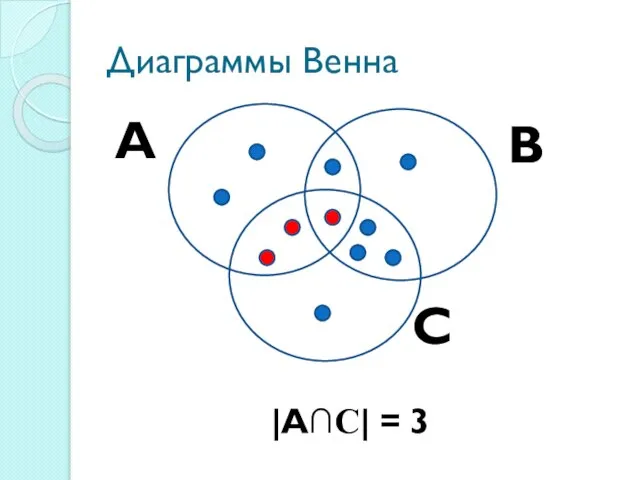
Слайд 27Обозначения
А∩С – множество студентов группы
азПСОу-108, занимающихся перетягиванием каната и синхронным плаванием
|

А∩С|=3
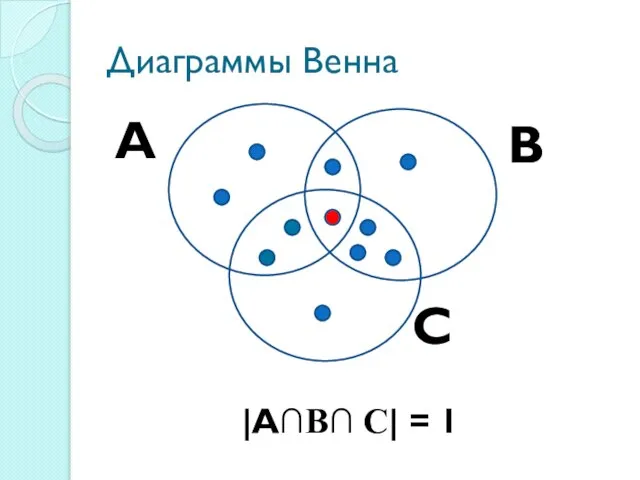
А∩В∩С – множество студентов группы азПСОу-108, занимающихся всеми тремя видами спорта
| А∩В∩С|=1
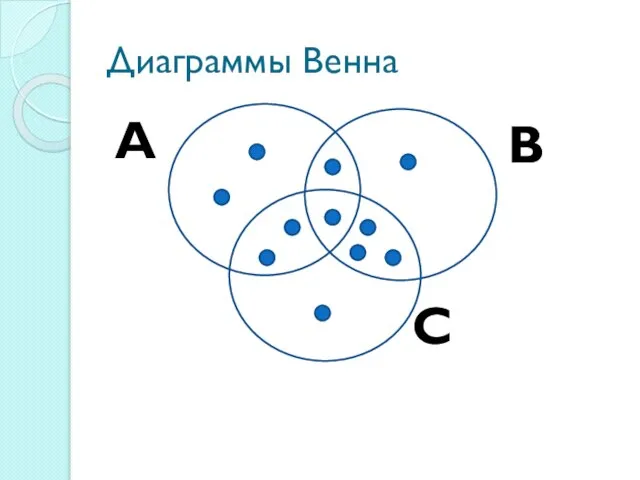
Слайд 28Диаграммы Венна
|А| = 6 |В| =6 |С| = 7
А
С
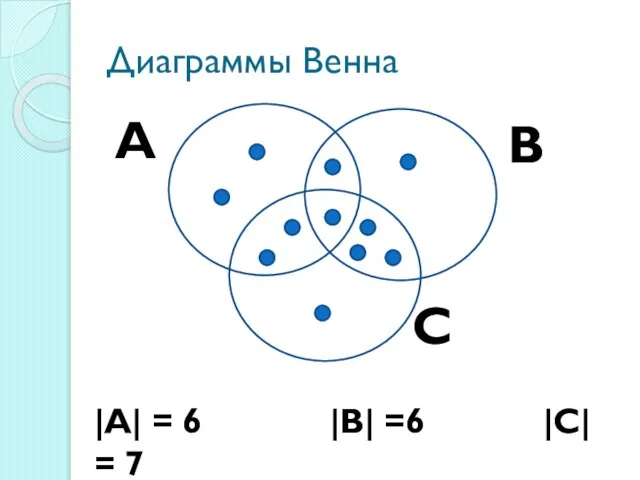
Слайд 32Формула мощности объединения трёх множеств
|АUВUС| =
=|А| +|В|+|С| -
-|А∩В| -|А∩С| -|С∩В|

Слайд 33Формула мощности объединения трёх множеств
|АUВUС| =
=6+6+7-2-4-3=10

Слайд 36Формула мощности объединения трёх множеств
|АUВUС| =
=|А| +|В|+|С| -
-|А∩В| -|А∩С| -|С∩В| +
+

|А∩В ∩С |
Слайд 37Формула мощности объединения трёх множеств
|АUВUС| =
=6+6+7-2-4-3+1=11

Слайд 38Задача 1V
Из 35 студентов, побывавших на каникулах в Москве, все, кроме двоих,

делились впечатлениями.
О посещении Большого театра с восторгом вспоминали 12 чел., Кремля – 14, а 16 – о концерте. По три студента запомнили посещение театра и Кремля, а также театра и концерта, четверо – концерта и пребывания в Кремле.
Сколько студентов сохранили воспоминания одновременно о театре, концерте и Кремле?
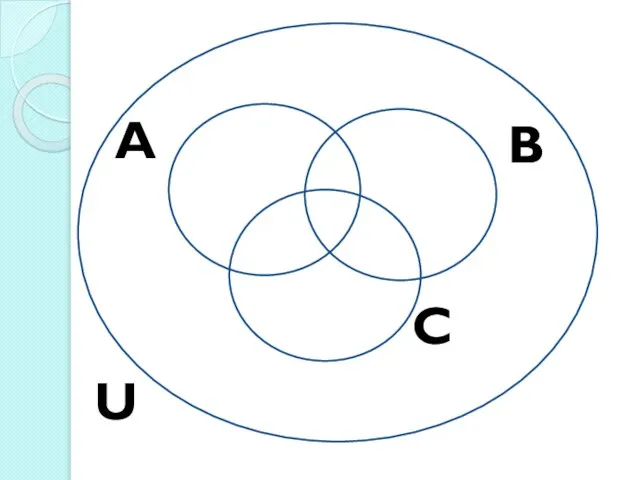
Слайд 40Обозначения
U – множество студентов, посетивших Москву – универсальное множество
|U|=35
А – множество

запомнивших Большой театр
|А|=12
В – множество студентов, рассказывавших о Кремле
|В|=14
Слайд 41Обозначения
С – множество студентов, вспоминавших о концерте
|С|=16
А∩В – множество тех, кто

рассказывал о Большом театре и Кремле
|А∩В |=3
А∩С – множество тех, кто делился впечатлениями о Большом театре и концерте
|А∩С |=3
Слайд 42Обозначения
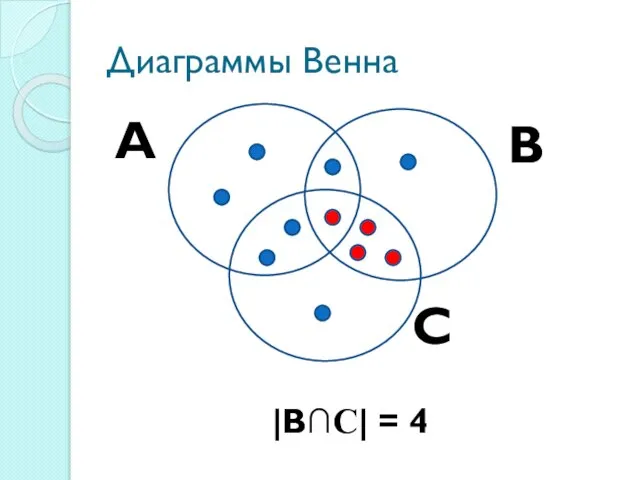
B∩С – множество тех, кто делился впечатлениями о Кремле и концерте
|B∩С

|=4
D = U /(АUВUС) – множество тех, кто не стал делиться воспоминаниями
| D|=2
А∩В∩С – множество тех, кто сохранил воспоминания о Большом театре, Кремле и концерте.
| А∩В∩С |=?
Слайд 43|А∩В∩С | =
|АUВUС| -|А| -|В|-|С| +
+|А∩В| +|А∩С| +|С∩В|
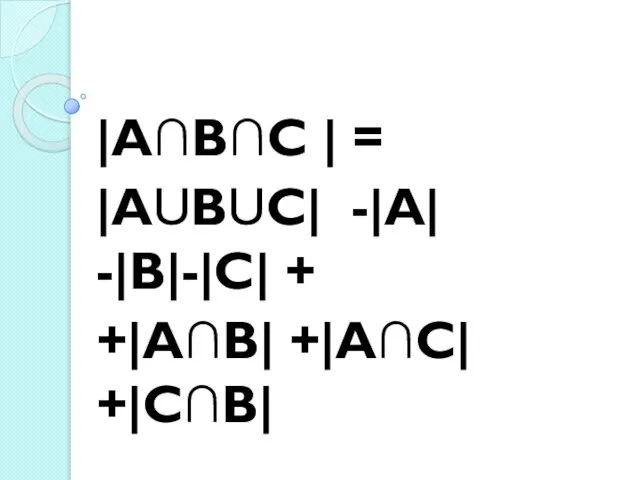
Слайд 44|А∩В∩С | =
|АUВUС| -|А| -|В|-|С| +
+|А∩В| +|А∩С| +|С∩В|










![Задача Даны числовые промежутки А= [-4; 5], В =(2; 6), С =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/367634/slide-10.jpg)

























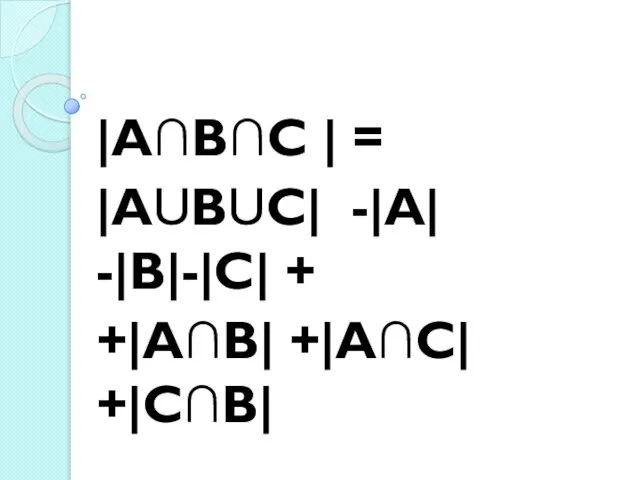

 Ход реализации пилотных проектов Росреестра на территории республики, а также создание региональной модели инфраструктуры прост
Ход реализации пилотных проектов Росреестра на территории республики, а также создание региональной модели инфраструктуры прост Пройдём с тобой по школьным этажам …
Пройдём с тобой по школьным этажам … Бал во дворце. Урок изобразительного искусства (5 класс)
Бал во дворце. Урок изобразительного искусства (5 класс) Биоинформатика
Биоинформатика Новоладожская детская школа искусств. Обучение детей росписи по ткани в технике холодного батика
Новоладожская детская школа искусств. Обучение детей росписи по ткани в технике холодного батика Кофейня «Blanco y negro»
Кофейня «Blanco y negro» ИНФОРМАЦИЯ О КОМПАНИИ
ИНФОРМАЦИЯ О КОМПАНИИ Презентация на тему Животный мир Арктики и Антарктиды
Презентация на тему Животный мир Арктики и Антарктиды  День полиции
День полиции Должностная инструкция
Должностная инструкция Подготовительные недели Великого Поста
Подготовительные недели Великого Поста Легко ли быть изобретателем?
Легко ли быть изобретателем? Итоговая аттестация выпускников старшей школы. ГОУСОШ №820
Итоговая аттестация выпускников старшей школы. ГОУСОШ №820 28-я Международная специализированная выставка Реклама 2021
28-я Международная специализированная выставка Реклама 2021 What are they wearing gtame
What are they wearing gtame Спешите стать терпимей и добрей
Спешите стать терпимей и добрей Презентация на тему Слово Предложение
Презентация на тему Слово Предложение Политическая система общества
Политическая система общества  Презентация на тему Любовная лирика Пушкина
Презентация на тему Любовная лирика Пушкина  «Алфавит - животные» (в загадках и картинках)
«Алфавит - животные» (в загадках и картинках) Палеозой
Палеозой Игра «Знатоки квадратных уравнений»
Игра «Знатоки квадратных уравнений» Ledeco – профессиональный партнер в сфере реализации инженерно-строительных проектов
Ledeco – профессиональный партнер в сфере реализации инженерно-строительных проектов дз
дз Риски информационной безопасности при передаче систем на аутсорсинг
Риски информационной безопасности при передаче систем на аутсорсинг Политический анализ
Политический анализ Штефан Кукс Stephan Kux Отдел Экономики Economic Development Кантон Цюрих Canton of Zurich
Штефан Кукс Stephan Kux Отдел Экономики Economic Development Кантон Цюрих Canton of Zurich  Стажировка в АО Сибур-Нефтехим (специалист планово-экономического отдела)
Стажировка в АО Сибур-Нефтехим (специалист планово-экономического отдела)