Содержание
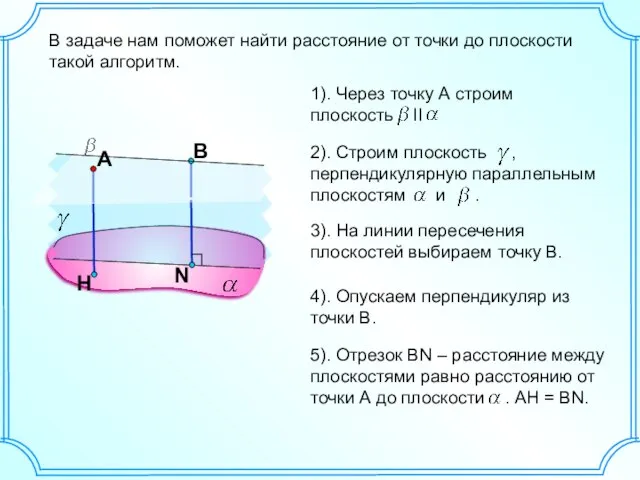
- 2. В задаче нам поможет найти расстояние от точки до плоскости такой алгоритм. 3). На линии пересечения
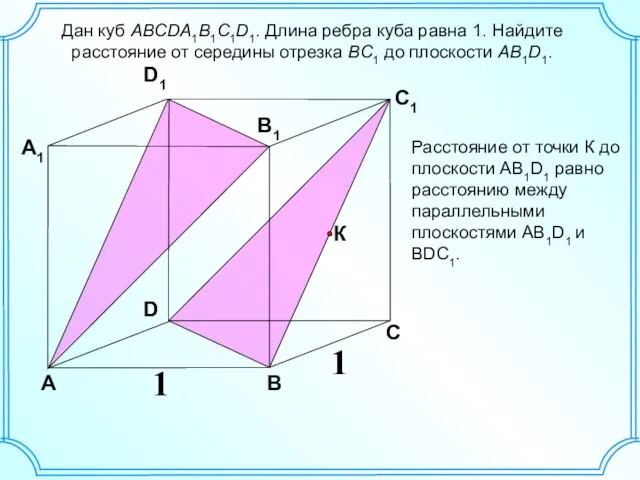
- 3. Дан куб ABCDA1B1C1D1. Длина ребра куба равна 1. Найдите расстояние от середины отрезка BC1 до плоскости
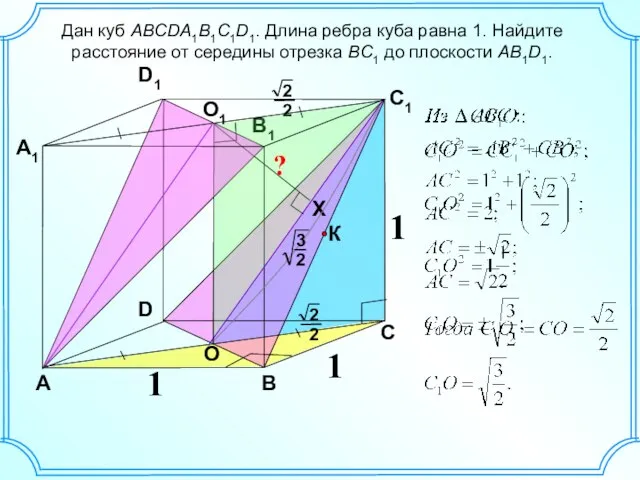
- 4. Дан куб ABCDA1B1C1D1. Длина ребра куба равна 1. Найдите расстояние от середины отрезка BC1 до плоскости
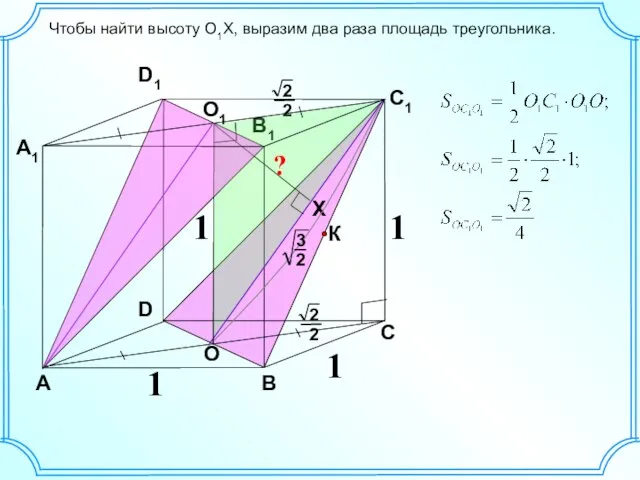
- 5. D А В С А1 D1 С1 В1 1 1 К O1 O 1 ? 1
- 7. Скачать презентацию
 Абсолютные и относительные величины
Абсолютные и относительные величины МЛМ — это бизнес статистики, а не убеждений
МЛМ — это бизнес статистики, а не убеждений Современные методы управления жизненным циклом самолета
Современные методы управления жизненным циклом самолета Бизнес-схемы и бизнес-процессы. Организация эффективного управления
Бизнес-схемы и бизнес-процессы. Организация эффективного управления Программа создания национального домена .РФ на основе кириллицы Андрей Колесников АНО «Координационный центр национального доме
Программа создания национального домена .РФ на основе кириллицы Андрей Колесников АНО «Координационный центр национального доме Типы химических реакций
Типы химических реакций Презентация на тему О растениях и организмов в почве
Презентация на тему О растениях и организмов в почве  Театр и музыка Древней Греции
Театр и музыка Древней Греции Алхимики
Алхимики ФИЗИОЛОГИЯ БАКТЕРИЙ
ФИЗИОЛОГИЯ БАКТЕРИЙ Медиаметрические исследования целевой аудитории для различных СМИ
Медиаметрические исследования целевой аудитории для различных СМИ ТЕХНИКА ДЛЯ ПРОИЗВОДСТВА НАТУРАЛЬНЫХ СОКОВ И НЕКТАРОВ
ТЕХНИКА ДЛЯ ПРОИЗВОДСТВА НАТУРАЛЬНЫХ СОКОВ И НЕКТАРОВ Vánoce v České republice
Vánoce v České republice Прибавление числа 2. Закрепление пройденного
Прибавление числа 2. Закрепление пройденного Бизнес от А до Я
Бизнес от А до Я Государственное общеобразовательное учреждение РК Физико-математический лицей-интернат
Государственное общеобразовательное учреждение РК Физико-математический лицей-интернат Культура общения
Культура общения Так ли обыкновенны обыкновенные дроби
Так ли обыкновенны обыкновенные дроби А.П.Чехов – несравненный художник жизни
А.П.Чехов – несравненный художник жизни Экономическое развитие. Экономическая деятельность и условия её эффективности.
Экономическое развитие. Экономическая деятельность и условия её эффективности. Маркетинговая деятельность на предприятиях
Маркетинговая деятельность на предприятиях Андрианова Наталия ВалериевнаПрезентация учителя ИЗОМОУ «Гимназия №6»г. Новочебоксарск
Андрианова Наталия ВалериевнаПрезентация учителя ИЗОМОУ «Гимназия №6»г. Новочебоксарск Взаимодействие генов. Сцепленное наследование
Взаимодействие генов. Сцепленное наследование Портрет на фоне малой Родины
Портрет на фоне малой Родины Отчет о работе Бабаевского местного отделения политической партии Единая Россия
Отчет о работе Бабаевского местного отделения политической партии Единая Россия 1000 мелочей + ElMindMap для электронного обучения Идея: Дюсьмикеев Андрей Решение: Сизонов Олег. - презентация
1000 мелочей + ElMindMap для электронного обучения Идея: Дюсьмикеев Андрей Решение: Сизонов Олег. - презентация Понятие правоотношения
Понятие правоотношения «Потенциал энергоэффективности в домашнем хозяйстве – состояние и перспективные возможности».
«Потенциал энергоэффективности в домашнем хозяйстве – состояние и перспективные возможности».