Нормальное распределение

Вопросы для обсуждения
Случайная величина и ее распределение
Математическое ожидание и его оценка
Дисперсия и ее оценка
Анормальные модели распределения. Асимметрия и эксцесс распределения

ВОПРОС №1
Случайная величина и ее распределение

Генеральная совокупность
Генеральная совокупность – все множество объектов, по поводу которого строится рассуждение теоретика.
Генеральная совокупность – как правило, не имеет четко очерченных границ.

Выборка
Выборка – часть генеральной совокупности, ее статистическая модель.
Выборка – должна максимально точно соответствовать генеральной совокупности. Как правило, это достигается за счет применения различных процедур рандомизации.
Иными словами, выборка – это случайная модель генеральной совокупности, которая может быть отождествлена с ней лишь с определенной долей вероятности.

Случайная величина
Случайные величины связаны со случайными событиями.
О случайных событиях говорят тогда, когда оказывается невозможным однозначно предсказать результат, который может быть получен в тех или иных условиях.

Случайные величины
Дискретная
Может принимать конкретные значения из ограниченного множества.
Набор значений ограничен, фиксирован.
Непрерывная
Может принимать неопределенный набор значений из фиксированного множества.
Набор значений неограничен, случаен.

Моделирование случайных событий
Теория вероятностей и математическая статистика исследуют законы, описывающие поведение случайных величин, как дискретных, так и непрерывных.
Такие законы отражают оценку вероятности того или иного значения случайной величины, что обычно обозначают как распределение случайной величины.

Нормальное распределение
Нормальное распределение имеет место тогда, когда интересующее нас явление подвержено влиянию бесконечного числа случайных факторов, уравновешивающих друг друга.

Z-распределение
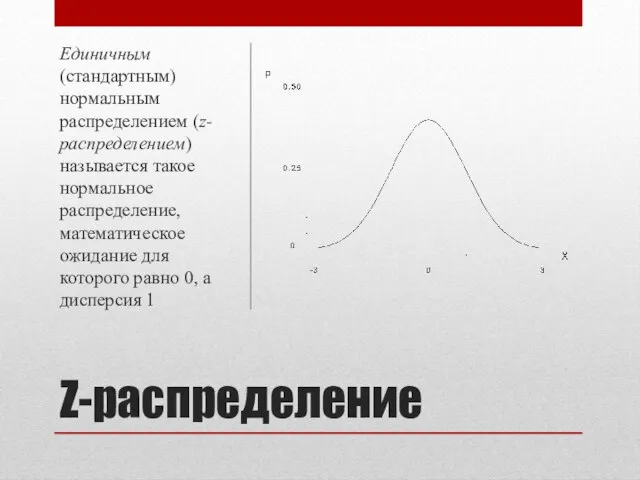
Единичным (стандартным) нормальным распределением (z-распределением) называется такое нормальное распределение, математическое ожидание для которого равно 0, а дисперсия 1

Параметры распределения

ВОПРОС №2
Математическое ожидание и его оценка

Математическое ожидание
Математическим ожиданием в математической статистике обозначают центральный момент первого порядка.

Оценка математического ожидания

Среднее арифметическое
Наиболее часто используемая оценка математического ожидания.
Предполагает, что результат измерения задан в метрической шкале.
Является несмещенной оценкой математического ожидания, т.е. ожидаемое значение этой величины равно математическому ожиданию.

Мода
Обычно используется в случае, когда набор значений случайной величины ограничен и имеется большое число повторяющихся значений.
Является несмещенной оценкой математического распределения.
Если два значения в выборке встречаются одинаково часто, то такое распределение называют бимодальным.
Если все значения в выборке встречаются одинаково часто, то такая выборка не имеет моды.

Медиана
Частный случай квантиля распределения.
Квантиль распределения определяют как интегральное значение распределения между двумя величинами переменной X.
Таким образом, величина X будет являться медианой распределения, если интегральное значение распределения от -∞ до X равно интегральному значению распределения от X до +∞.
Медиана также является несмещенной оценкой математического ожидания.

ВОПРОС №3
Дисперсия и ее оценка

Дисперсия

Оценка дисперсии
Где:
x – результаты измерения случайной величины, n – объем выборки, s2- оценка дисперсии

Оценка по выборке
Так как оценка дисперсии в приведенной ранее формуле осуществляется относительно среднего по выборке, полученная статистика s2 оказывается смещенной относительно истинного значения дисперсии σ2, т.е.:

Оценка по генеральной совокупности
Чтобы получить оценку дисперсии для генеральной совокупности, необходимо воспользоваться следующей формулой:

Стандартное отклонение
На практике вместо оценки дисперсии чаще используют производную от нее – стандартное отклонение, иначе называемое средне-квадратичным отклонением (уклонением).
Значение стандартного отклонения определяется как квадратный корень от величины дисперсии.

ВОПРОС №4
Анормальные модели распределения. Асимметрия и эксцесс распределения

Анормальное распределение
Нормальное распределение имеет место, когда на интересующее нас явление оказывают влияние неопределенное множество неконтролируемых факторов, которые уравновешивают друг друга.
Если в ходе измерения действует какой-либо однонаправленный фактор, распределение случайной величины может отличаться от закона нормального распределения.
Для описания распределения, отличающегося от нормального, необходимо учесть моменты более высокого порядка – асимметрию и эксцесс.

Асимметрия
Асимметрия представляет собой момент третьего порядка, т.е., говоря неформальным языком, представляет собой дисперсию дисперсии.
На графике асимметрия проявляет себя как степень скошенности распределения в положительную (положительная асимметрия) или отрицательную (отрицательная асимметрия) сторону.

Пример: асимметрия времени реакции
При измерении времени реакции испытуемого неминуемо получается положительная асимметрия ответов, так как испытуемый не может реагировать быстрее известного предела, но может бесконечно замедлять реакцию.

Эксцесс
Эксцесс представляет собой момент четвертого порядка.
Об эксцессе наглядно можно судить по степени «выпуклости» или «заостренности» распределения.

Примеры эксцесса
Положительный
Отрицательный