Описательные характеристики распределения тестовых результатов

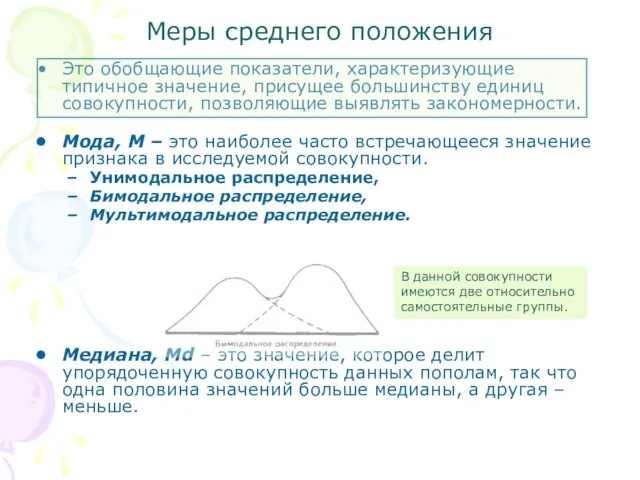
Это обобщающие показатели, характеризующие типичное значение, присущее большинству единиц совокупности, позволяющие выявлять закономерности.
Мода, М – это наиболее часто встречающееся значение признака в исследуемой совокупности.
Унимодальное распределение,
Бимодальное распределение,
Мультимодальное распределение.
Медиана, Мd – это значение, которое делит упорядоченную совокупность данных пополам, так что одна половина значений больше медианы, а другая – меньше.
Меры среднего положения
В данной совокупности имеются две относительно самостоятельные группы.

Среднее, , – это значение, которое отражает типичное значение для исследуемой совокупности в данных условиях:
где n – объем совокупности, xi – i-е значение совокупности.
Чтобы средняя величина была действительно обобщающей характеристикой, улавливающей закономерность, она должна применяться к достаточно однородной совокупности.
Средняя величина рассчитывается только для количественных признаков.
Меры среднего положения

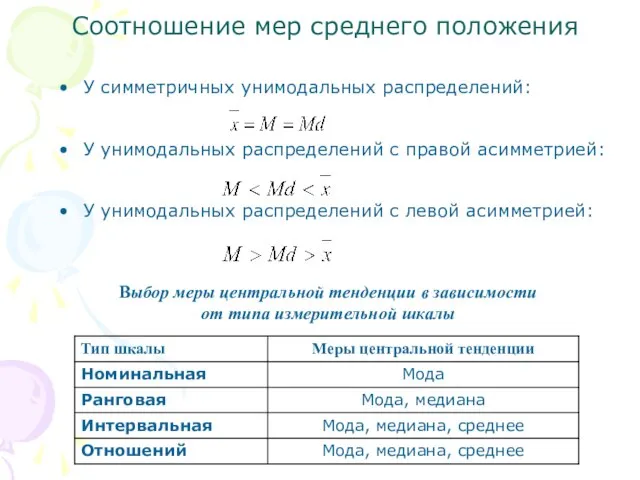
У симметричных унимодальных распределений:
У унимодальных распределений с правой асимметрией:
У унимодальных распределений с левой асимметрией:
Соотношение мер среднего положения
Выбор меры центральной тенденции в зависимости
от типа измерительной шкалы

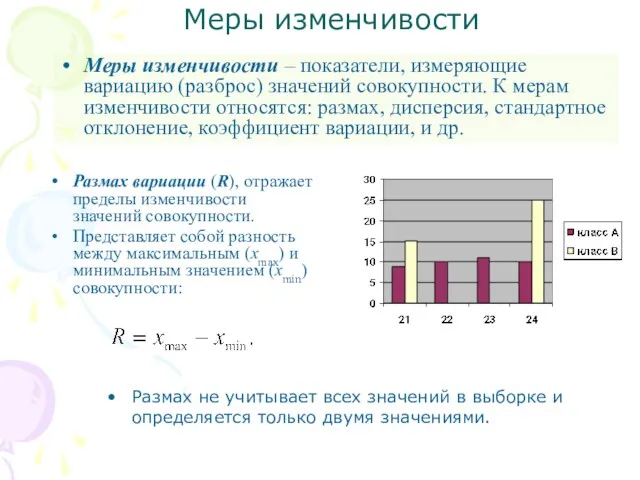
Меры изменчивости
Меры изменчивости – показатели, измеряющие вариацию (разброс) значений совокупности. К мерам изменчивости относятся: размах, дисперсия, стандартное отклонение, коэффициент вариации, и др.
Размах вариации (R), отражает пределы изменчивости значений совокупности.
Представляет собой разность между максимальным (xmax) и минимальным значением (xmin) совокупности:
Размах не учитывает всех значений в выборке и определяется только двумя значениями.

Дисперсия, , – это значение, которое отражает внутреннюю изменчивость значений исследуемой совокупности:
где n – объем совокупности,
xi – i-е значение, – среднее значение.
Стандартное отклонение, , показывает насколько в среднем отклоняется каждое значение (xi ) от среднего :
Меры изменчивости

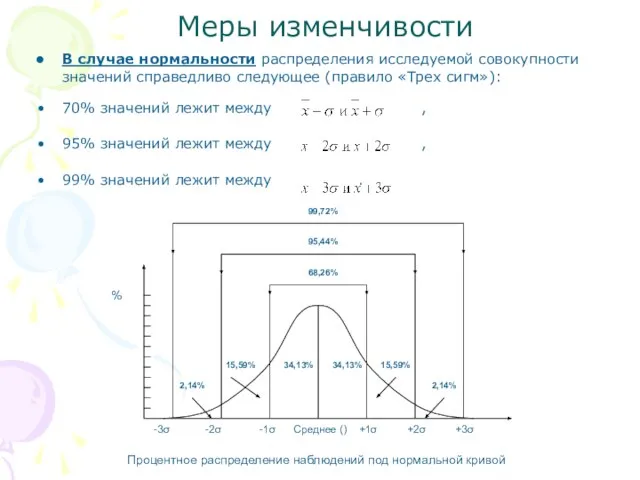
Меры изменчивости
В случае нормальности распределения исследуемой совокупности значений справедливо следующее (правило «Трех сигм»):
70% значений лежит между ,
95% значений лежит между ,
99% значений лежит между .

Меры изменчивости

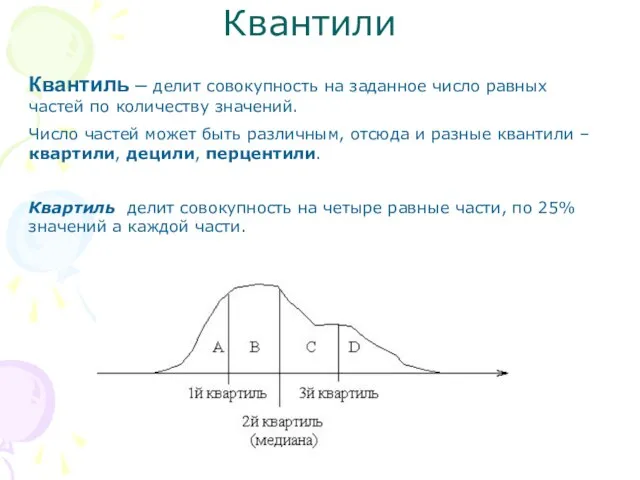
Квантили
Квантиль – делит совокупность на заданное число равных частей по количеству значений.
Число частей может быть различным, отсюда и разные квантили – квартили, децили, перцентили.
Квартиль делит совокупность на четыре равные части, по 25% значений а каждой части.

Квантили
Дециль делит совокупность на 10 равных частей, по 10% значений в каждой части.
Перцентиль делит совокупность на 100 равных частей.
Например,
D1 = C10, Q1 = C25, Md = C50, Q3 = C75 и т.д.
Необходимость расчета квантилей вызвана теми же причинами, что и расчет медианы: низкая чувствительность к случайным резким отклонениям значений признака.

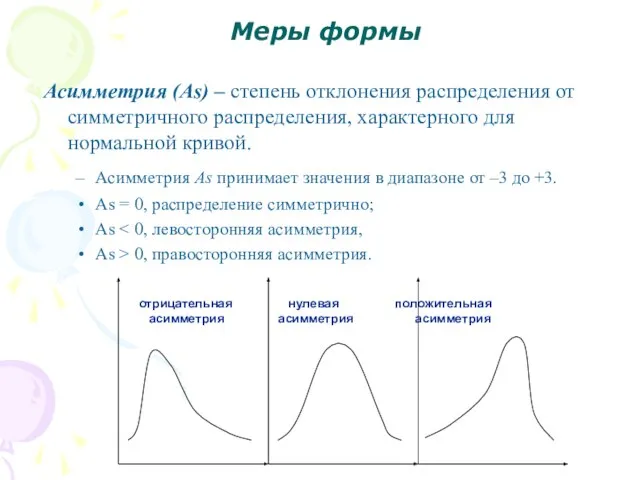
Меры формы
Асимметрия (As) – степень отклонения распределения от симметричного распределения, характерного для нормальной кривой.
Асимметрия As принимает значения в диапазоне от –3 до +3.
As = 0, распределение симметрично;
As < 0, левосторонняя асимметрия,
As > 0, правосторонняя асимметрия.

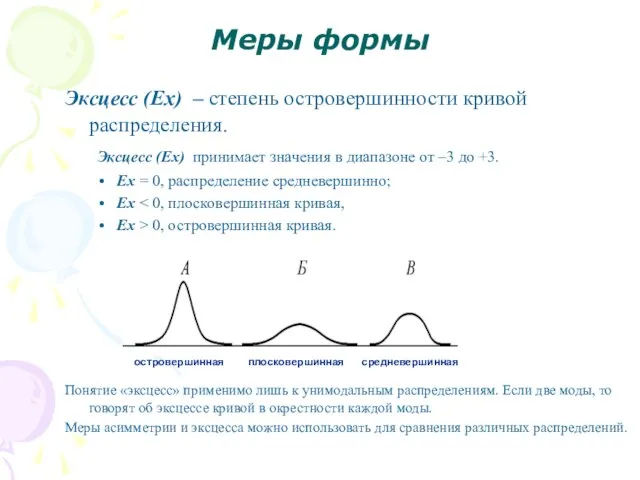
Меры формы
Эксцесс (Ex) – степень островершинности кривой распределения.
Эксцесс (Ex) принимает значения в диапазоне от –3 до +3.
Ex = 0, распределение средневершинно;
Ex < 0, плосковершинная кривая,
Ex > 0, островершинная кривая.
Понятие «эксцесс» применимо лишь к унимодальным распределениям. Если две моды, то говорят об эксцессе кривой в окрестности каждой моды.
Меры асимметрии и эксцесса можно использовать для сравнения различных распределений.
островершинная плосковершинная средневершинная

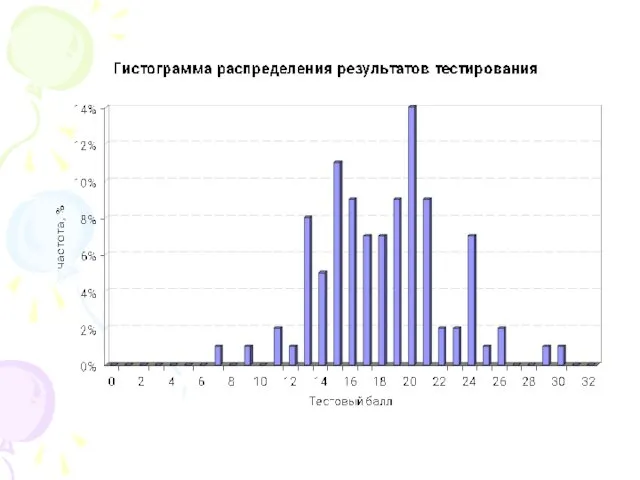
План апробации тестовых заданий