Слайд 2Предмет теории вероятностей.
Теория вероятностей изучает закономерности, возникающие в случайных экспериментах.
Случайным

называют эксперимент, результат которого нельзя предсказать заранее.
Невозможность предсказать результат отличает случайное явление от детерминированного.
Слайд 3Предмет теории вероятностей.
Не все случайные явления (эксперименты) можно изучать методами теории

вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях.
Слайд 4Предмет теории вероятностей.
И в случайных экспериментах наблюдаются некоторые закономерности, например свойство

«статистической устойчивости»: если A — некоторое событие, могущее произойти или не произойти в результате эксперимента, то доля n(A) /n экспериментов, в которых данное событие произошло, имеет тенденцию стабилизироваться с ростом общего числа экспериментов n, приближаясь к некоторому числу P(A).
Слайд 5Пространство элементарных исходов.
Определение 1. Пространством элементарных исходов («омега») называется множество, содержащее все

возможные результаты данного случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой («омега»).
Слайд 6Пространство элементарных исходов.
Определение 2. Событиями мы будем называть подмножества множества Говорят, что

в результате эксперимента произошло событие если в эксперименте произошел один из элементарных исходов, входящих в множество
Слайд 7Пространство элементарных исходов.

Слайд 8Пространство элементарных исходов.
Определение 3.
1. Достоверным называется событие, которое обязательно происходит в

результате эксперимента, т. е. единственное событие, включающее все элементарные исходы — событие
2. Н е в о з м о ж н ы м называется событие, которое не может произойти в результате эксперимента, т. е. событие, не содержащее ни одного элементарного исхода («пустое множество» ). Заметим, что всегда
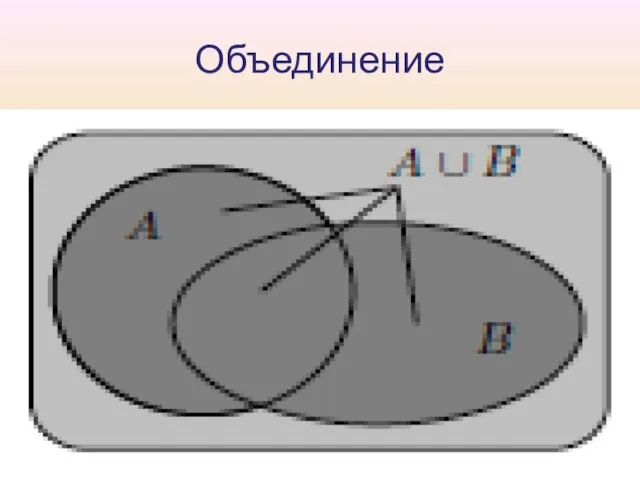
Слайд 9Объединение событий
Определение 4. 1. Объединением A U B событий A и B

называется событие, состоящее в том, что произошло либо A, либо B, либо оба события одновременно. На языке теории множеств A U B есть множество, содержащее как элементарные исходы из множества A, так и элементарные исходы из множества B
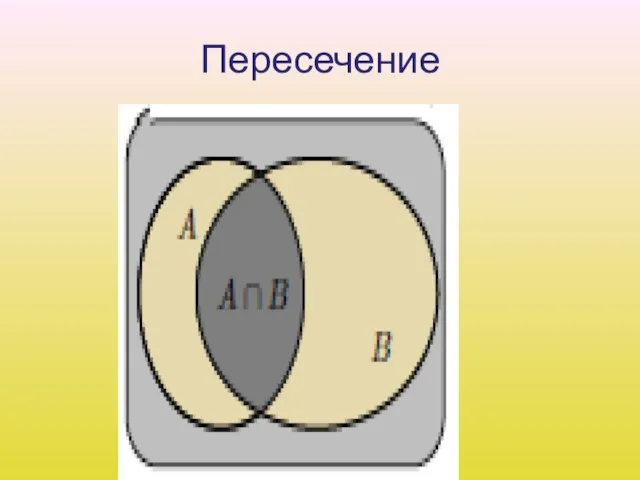
Слайд 11Пересечение событий
2. Пересечением A B событий A и B называется событие, состоящее в

том, что произошли оба события A и B одновременно. На языке теории множеств A B есть множество, содержащее элементарные исходы, входящие в пересечение множеств A и B.
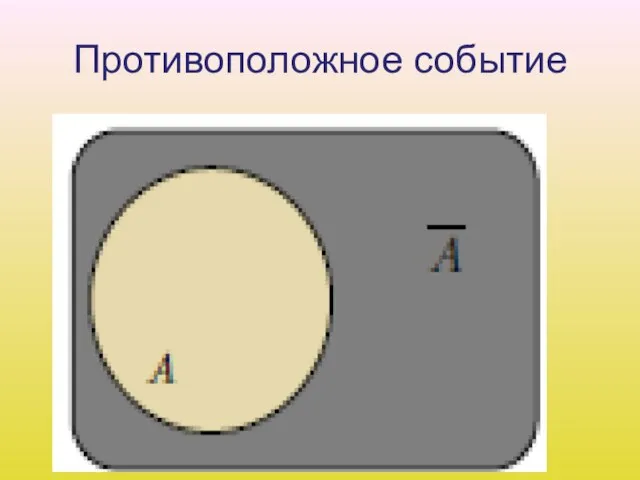
Слайд 13Противоположное событие
3. П р о т и в о п о л о

ж н ы м (или дополнительным) к событию A называется событие состоящее в том, что событие A в результате эксперимента не произошло. Т. е. множество состоит из элементарных исходов, не входящих в A.
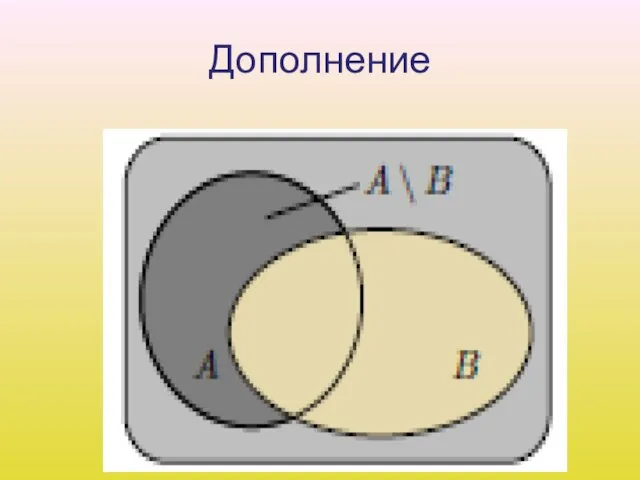
Слайд 15Дополнение
4. Дополнением A\B события B до A называется событие, состоящее в том, что

произошло событие A, но не произошло B. Т. е. множество A\B содержит элементарные исходы, входящие в множество A, но не входящие в B.
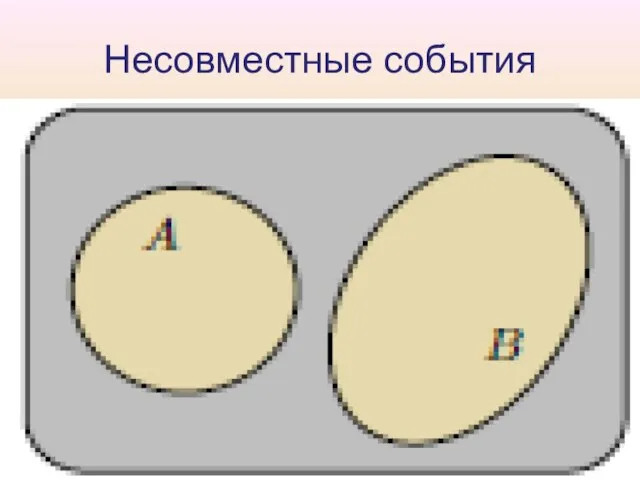
Слайд 17Несовместные события
Определение 5.
1. События A и B называют несовместными, если
2. События называются попарно

несовместными, если для любых i = j, где события
несовместны.
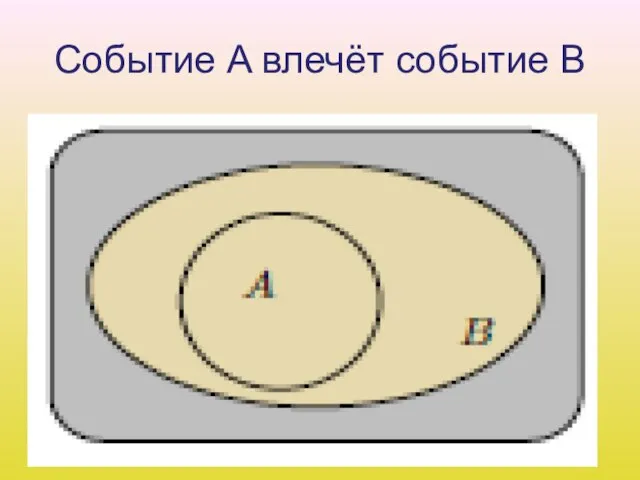
Слайд 19Событие A влечёт событие B
3. Говорят, что событие A влечёт событие B, и

пишут если всегда, как только происходит событие A, происходит и событие B. На языке теории множеств это означает, что любой элементарный исход, входящий в множество A, одновременно входит и в множество B, т. е. A содержится в B.
Слайд 21Вероятность на дискретном пространстве элементарных исходов
Пространство элементарных исходов назовём дискретным, если оно

конечно или счётно:
Множество счётно, если существует взаимно-однозначное соответствие между этим множеством и множеством всех натуральных чисел. Счётными множествами являются множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество чётных чисел и т.д. Множество конечно, если оно состоит из конечного числа элементов.
Слайд 22Вероятность на дискретном пространстве элементарных исходов
Чтобы определить вероятность любого события на дискретном

пространстве элементарных исходов, достаточно присвоить вероятность каждому элементарному исходу. Тогда вероятность любого события определяется как сумма вероятностей входящих в него элементарных исходов.
Слайд 25Классическое определение вероятности
Предположим, что мы имеем дело с пространством элементарных исходов, состоящим

из конечного числа N элементов:
Предположим, что из каких-либо соображений мы можем считать элементарные исходы равновозможными. Тогда вероятность любого из них принимается равной 1 / N.
Слайд 26Классическое определение вероятности

Слайд 27Классическое определение вероятности
Определение 7. Говорят, что эксперимент удовлетворяет «классическому определению вероятности», если

пространство элементарных исходов состоит из конечного числа = N равновозможных исходов. В этом случае вероятность любого события A вычисляется по формуле
называемой классически м о п р е де л е н и е м
в е р о я т н о с т и.
Слайд 28Классическое определение вероятности
Формулу
читают так: «вероятность события A равна от-ношению числа исходов, благоприятствующих

событию A, к общему числу исходов».
Полезно сравнить это определение с классической формулировкой Якоба Бернулли : «Вероятность есть степень достоверности и отличается от неё как часть от целого»
Слайд 29Гипергеометрическое распределение

Слайд 30Гипергеометрическое распределение
Здесь мы в первый, но далеко не в последний раз встретились

с термином «распределение» вероятностей. Это слово всегда обозначает некий способ разделить (распределить) общую единичную вероятность между какими-то точками или множествами на вещественной прямой.























 Реклама вуза в городской среде как элемент продвижения бренда РГУПС
Реклама вуза в городской среде как элемент продвижения бренда РГУПС Хэллоуин
Хэллоуин PC Iliyas
PC Iliyas Электромагнитная индукция. Закон электромагнитной индукции.
Электромагнитная индукция. Закон электромагнитной индукции. ЧИСЛО е ЭКСПОНЕНТА НАТУРАЛЬНЫЙ ЛОГАРИФМ
ЧИСЛО е ЭКСПОНЕНТА НАТУРАЛЬНЫЙ ЛОГАРИФМ Remembrance day
Remembrance day Табличка. Кабинет №1
Табличка. Кабинет №1 Инсталляции В2С за период с 23.08 по 29.08.2021
Инсталляции В2С за период с 23.08 по 29.08.2021 Знакомьтесь !!! Кременская Центральная Районная Библиотека
Знакомьтесь !!! Кременская Центральная Районная Библиотека Звон колоколов Саратовского района
Звон колоколов Саратовского района Информация ее виды и свойства
Информация ее виды и свойства Конное троеборье
Конное троеборье Статуэтки
Статуэтки Солнечные батареиВведение
Солнечные батареиВведение Какие регионы России могут измениться
Какие регионы России могут измениться MS EAS experience2006-2011
MS EAS experience2006-2011 Тур по Южному Уралу
Тур по Южному Уралу Развитие навыков самоконтроля
Развитие навыков самоконтроля Маркетинговое исследование пакетированных соков в городе Новороссийск
Маркетинговое исследование пакетированных соков в городе Новороссийск Ассирийское железное царство
Ассирийское железное царство Черная металлургия России (9 класс)
Черная металлургия России (9 класс) Legal status of individuals
Legal status of individuals Презентация на тему Исторические ступени развития общества
Презентация на тему Исторические ступени развития общества Графическое представление газовых процессов
Графическое представление газовых процессов Энергоэффективные технологии и способы их внедрения в системы ЖКХ города
Энергоэффективные технологии и способы их внедрения в системы ЖКХ города Повторное использование асфальтобетона
Повторное использование асфальтобетона  Лекция 1
Лекция 1 Голодание
Голодание