Содержание
- 2. Выяснить какие знания из курса алгебры и геометрии требуются для решения задач на построение геометрических фигур
- 3. З А Д А Ч И Ознакомится с теорией построений изображений на компьютере при помощи «базовой
- 4. Поисковый метод с использованием научной и учебной литературы. Практический метод составления алгоритмов решения задач, и их
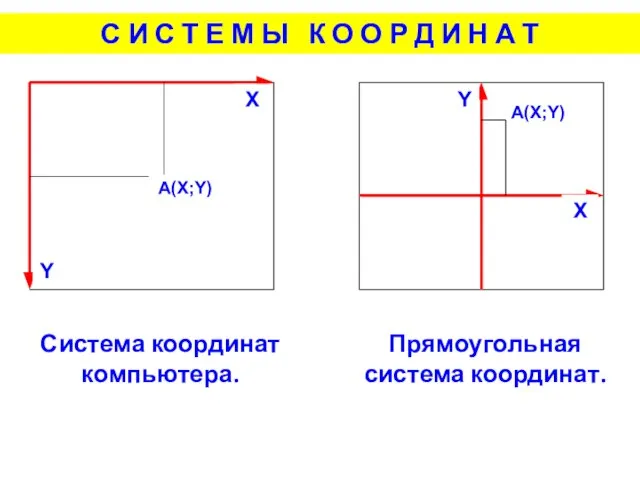
- 5. A(X;Y) X Y X Y Система координат компьютера. Прямоугольная система координат. С И С Т Е
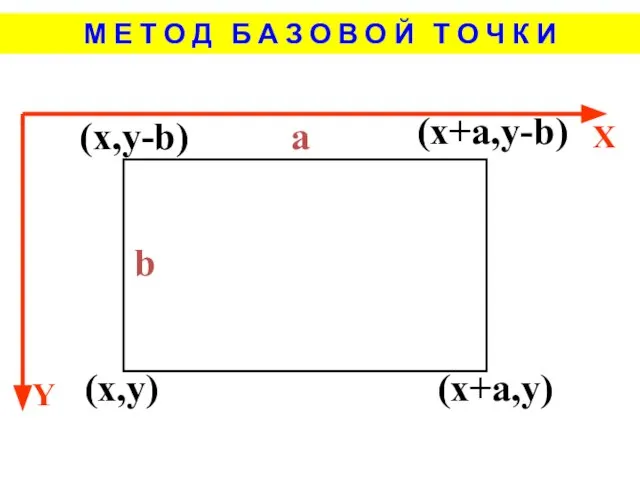
- 6. М Е Т О Д Б А З О В О Й Т О Ч К
- 7. Построение прямоугольного треугольника по двум катетам. Построение прямоугольного треугольника по катету и гипотенузе. Построение равностороннего треугольника.
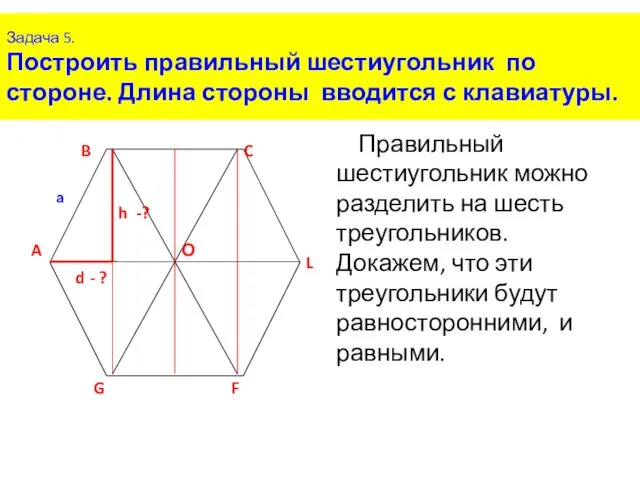
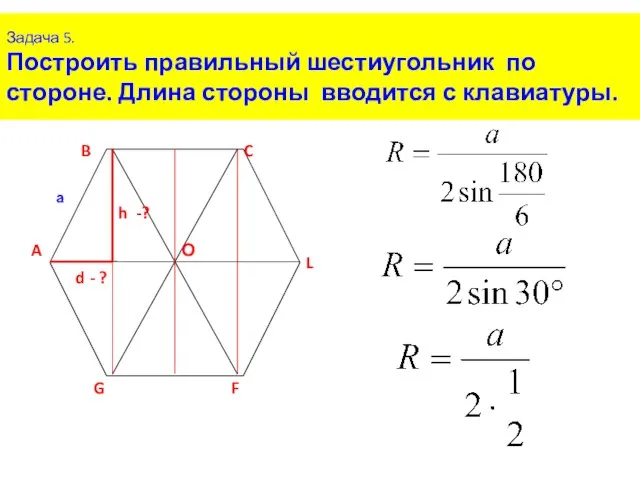
- 8. Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры. Правильный шестиугольник можно разделить
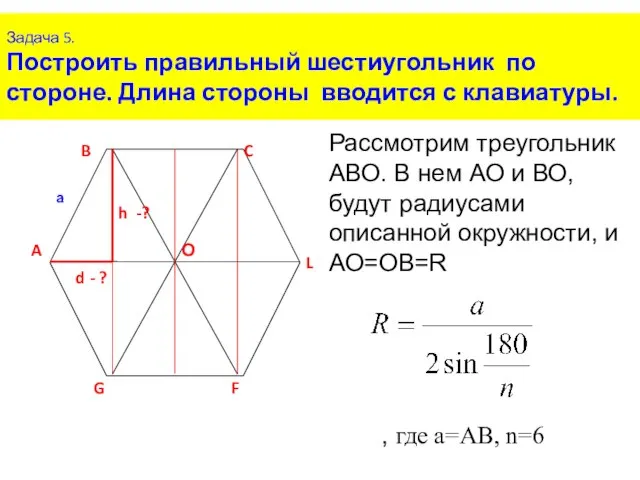
- 9. Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры. Рассмотрим треугольник АВО. В
- 10. Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры.
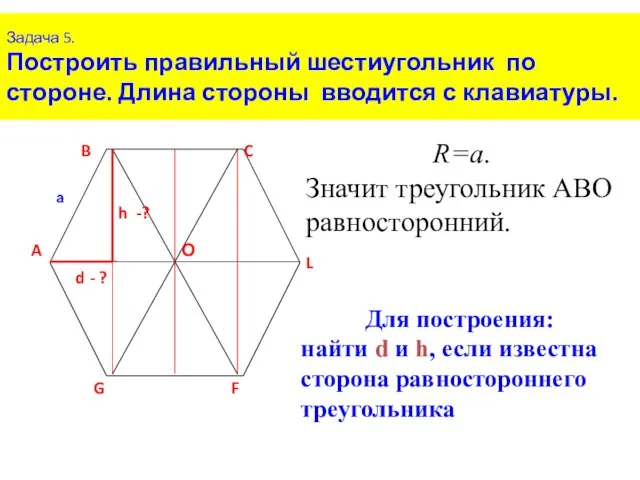
- 11. Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры. R=a. Значит треугольник АВО
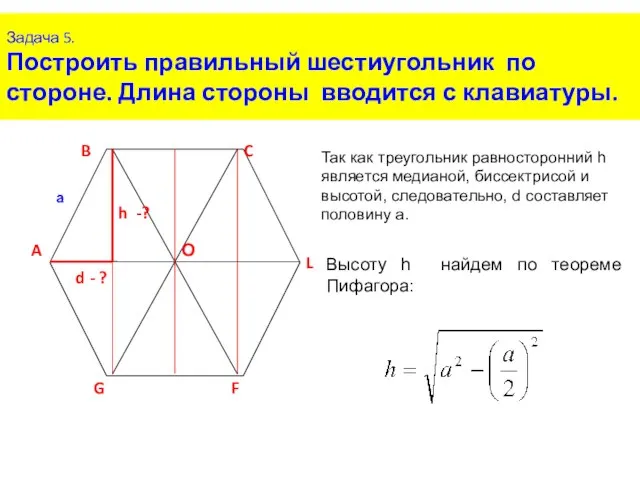
- 12. Задача 5. Построить правильный шестиугольник по стороне. Длина стороны вводится с клавиатуры. Высоту h найдем по
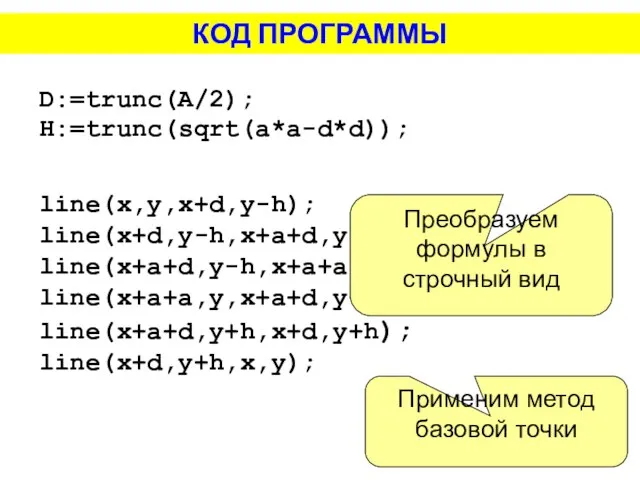
- 13. D:=trunc(A/2); H:=trunc(sqrt(a*a-d*d)); line(x,y,x+d,y-h); line(x+d,y-h,x+a+d,y-h); line(x+a+d,y-h,x+a+a,y); line(x+a+a,y,x+a+d,y+h); line(x+a+d,y+h,x+d,y+h); line(x+d,y+h,x,y); КОД ПРОГРАММЫ Преобразуем формулы в строчный вид Применим
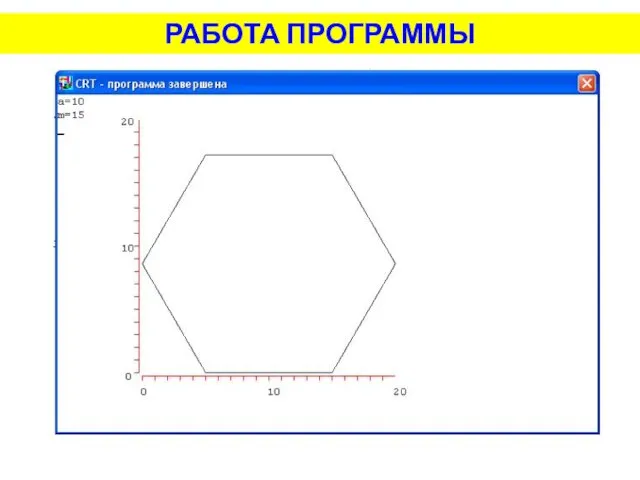
- 14. РАБОТА ПРОГРАММЫ
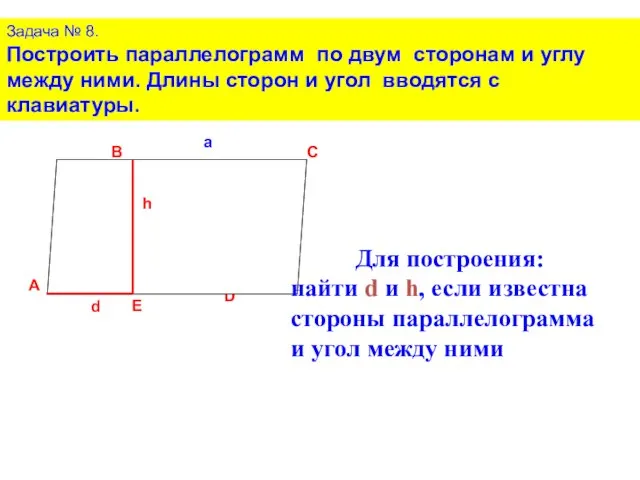
- 15. Задача № 8. Построить параллелограмм по двум сторонам и углу между ними. Длины сторон и угол
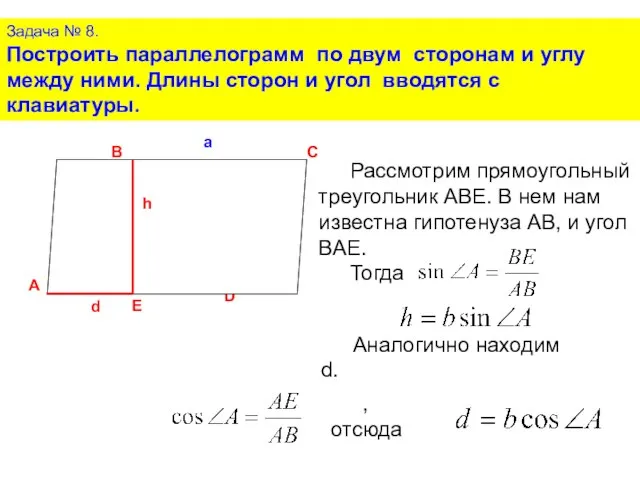
- 16. Задача № 8. Построить параллелограмм по двум сторонам и углу между ними. Длины сторон и угол
- 17. Задача № 8. Построить параллелограмм по двум сторонам и углу между ними. Длины сторон и угол
- 18. КОД ПРОГРАММЫ Преобразуем формулы в строчный вид Применим метод базовой точки n:=(n*pi)/180; h:=trunc(b*sin(n)); d:=trunc(b*cos(n)); line(x,y,x+d,y-h); line(x,y,x+a,y);
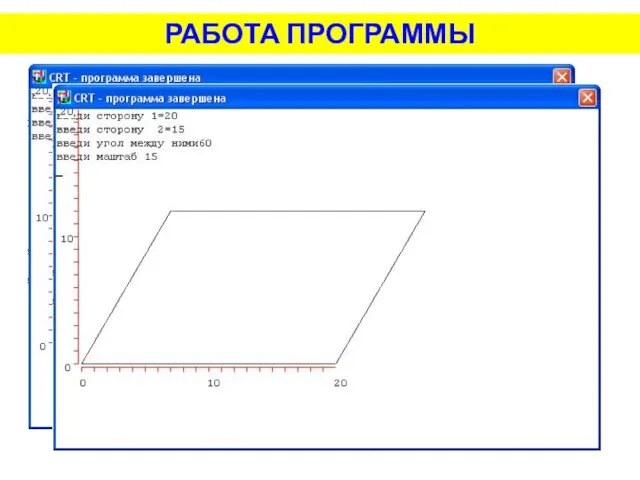
- 19. РАБОТА ПРОГРАММЫ
- 20. Для решения этих задач мне потребовались следующие математические знания: Треуго́льник— это геометрическая фигура, образованная тремя отрезками,
- 21. Для решения этих задач мне потребовались следующие математические знания: Окружность называется описанной около треугольника, если она
- 22. Для решения этих задач мне потребовались следующие математические знания: Формула для перевода градусов в радианы Радиус
- 23. Проанализировав решенные мною задачи, я выписал те теоремы, определения и формулы из курса алгебры и геометрии
- 24. Программирование компьютерной графики невозможно без знания математики. Для построения геометрических фигур используется специальный метод, «базовой точки».
- 26. Скачать презентацию











 Бизнес-процессы в индустрии питания
Бизнес-процессы в индустрии питания Методические рекомендации по приемам работы над С2.1 в ГИА 2012 года
Методические рекомендации по приемам работы над С2.1 в ГИА 2012 года Развивающая игра "Чего не хватает"
Развивающая игра "Чего не хватает" ОЧЕНЬ СЕРЬЕЗНЫЕ ИГРУШКИ
ОЧЕНЬ СЕРЬЕЗНЫЕ ИГРУШКИ Методы удаленного обучения
Методы удаленного обучения Планирование школьной клумбы.
Планирование школьной клумбы. Сущность взаимодействия классного руководителя с семьей
Сущность взаимодействия классного руководителя с семьей Оформление внешнего вида кафе
Оформление внешнего вида кафе Конвергентные и цифровые технологии
Конвергентные и цифровые технологии Инновационные технологии 21 века в области химической технологии.
Инновационные технологии 21 века в области химической технологии. ПРЕДОТВРАЩЕНИЕ КОНФЛИКТОВ ПРОФЕССИОНАЛЬНЫХ ИНТЕРЕСОВ В ХОДЕ АВТОМАТИЗИРОВАННОЙ КОНСТРУКТОРСКО-ТЕХНОЛОГИЧЕСКОЙ ПОДГОТОВКИ ПРО
ПРЕДОТВРАЩЕНИЕ КОНФЛИКТОВ ПРОФЕССИОНАЛЬНЫХ ИНТЕРЕСОВ В ХОДЕ АВТОМАТИЗИРОВАННОЙ КОНСТРУКТОРСКО-ТЕХНОЛОГИЧЕСКОЙ ПОДГОТОВКИ ПРО ВКР: Программно-информационная система оценки спроса на товары дистрибьюторской компании
ВКР: Программно-информационная система оценки спроса на товары дистрибьюторской компании Характер. Тема 7
Характер. Тема 7 Задачи знатокам
Задачи знатокам Арба парашиет. Четыре главы
Арба парашиет. Четыре главы Досуг группы продлённого дня 1 классов
Досуг группы продлённого дня 1 классов Дует, дует ветер. Рисование
Дует, дует ветер. Рисование Активизация познавательной деятельности на уроках биологии с использованием новых информационных технологий
Активизация познавательной деятельности на уроках биологии с использованием новых информационных технологий Презентация на тему Саша Черный Что ты тискаешь утенка
Презентация на тему Саша Черный Что ты тискаешь утенка Табличный процессор Microsoft Excel
Табличный процессор Microsoft Excel  Басни 3 класс
Басни 3 класс СМС инфо. Инструкция копилка
СМС инфо. Инструкция копилка Синтаксис. Повторение
Синтаксис. Повторение Физика Солнца
Физика Солнца Презентация на тему БОРЬБА ЗА СУЩЕСТВОВАНИЕ
Презентация на тему БОРЬБА ЗА СУЩЕСТВОВАНИЕ Руководство проведением мероприятий и торговых выставок
Руководство проведением мероприятий и торговых выставок Стрекозы
Стрекозы Инновация в Биатлоне
Инновация в Биатлоне