Содержание
- 2. «Let’s Make a Deal» Парадо́кс Мо́нти Хо́лла — одна из известных задач теории вероятностей, решение которой,
- 3. Формулировка задачи: Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трех
- 4. Решение по теореме Байеса где P(Aj) — априорная вероятность гипотезы Aj; P(Aj | B) — вероятность
- 5. В данной задаче N = 3, гипотезы: A1 — «автомобиль за дверью 1»; A2 — «автомобиль
- 6. Ход решения По формуле условной вероятности Подставим это выражение в формулу Байеса Условие задачи подразумевает, что
- 7. Это означает, что P(C | A1) = P(C | A2) = P(C | A3) = P(C)
- 8. Допущения: Первое: если игрок выбрал дверь 1, и автомобиль находится за дверью 1, то мы считаем,
- 9. Второе допущение позволяет сократить дробь и получить формулу В согласии с первым допущением получаем результат:
- 10. Ответ к задаче Правильным ответом к этой задаче является следующее: да, шансы выиграть автомобиль увеличиваются в
- 11. Более интуитивно понятное рассуждение: Пусть игрок действует по стратегии «изменить выбор». Тогда проиграет он только в
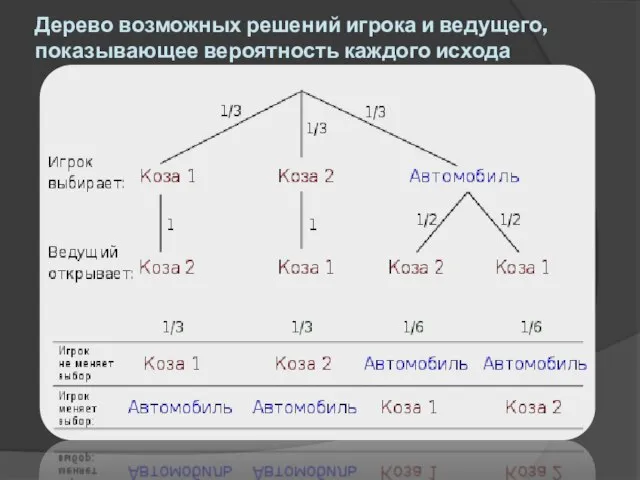
- 12. Дерево возможных решений игрока и ведущего, показывающее вероятность каждого исхода
- 15. Скачать презентацию











 Аральское море
Аральское море Социальная психология
Социальная психология Педагогические Lookи
Педагогические Lookи Фізика754
Фізика754 Презентация на тему Равнодействующая сила
Презентация на тему Равнодействующая сила  Духовно – нравственные основы развития личности
Духовно – нравственные основы развития личности Мариинский театр. Владивосток
Мариинский театр. Владивосток Будни и праздники начальной школы
Будни и праздники начальной школы Каша во рту
Каша во рту Добро, ласка, поощрение, требовательность, твердость, ограничение желаний в воспитании детей
Добро, ласка, поощрение, требовательность, твердость, ограничение желаний в воспитании детей Жизнь прожить – не поле перейти, или «Этапы большого пути»
Жизнь прожить – не поле перейти, или «Этапы большого пути»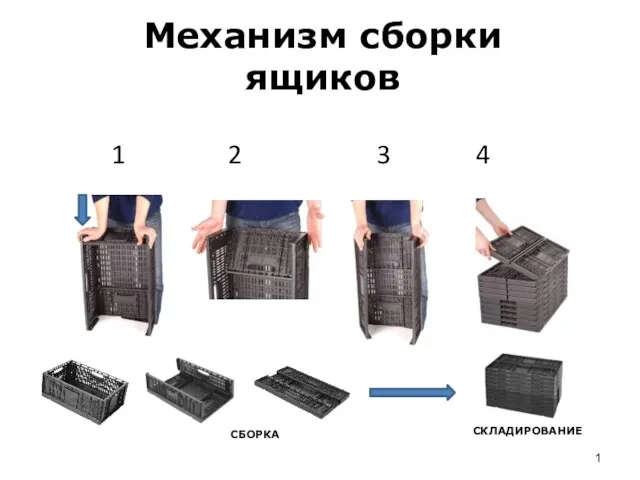 Механизм сборки ящиков
Механизм сборки ящиков « Распространение Реформации в Европе. Контрреформация»
« Распространение Реформации в Европе. Контрреформация» ПОЧЕМУ НУЖНО РАЦИОНАЛЬНО ИСПОЛЬЗОВАТЬ ЭНЕРГЕТИЧЕСКИЕ РЕСУРСЫ?
ПОЧЕМУ НУЖНО РАЦИОНАЛЬНО ИСПОЛЬЗОВАТЬ ЭНЕРГЕТИЧЕСКИЕ РЕСУРСЫ? Климат Тверской области
Климат Тверской области Мониторинг социальных настроений населения стран постсоветского пространства ЕМ-VI. Предварительные результаты 1 Проект «Евразий
Мониторинг социальных настроений населения стран постсоветского пространства ЕМ-VI. Предварительные результаты 1 Проект «Евразий Информационные компьютерные технологии в практике логопеда
Информационные компьютерные технологии в практике логопеда Презентация на тему путешествие Афанасия НИКИТИНА В ИНДИЮ 1466-1472
Презентация на тему путешествие Афанасия НИКИТИНА В ИНДИЮ 1466-1472  Конституция Российской Федерации
Конституция Российской Федерации Комедия А.С. Грибоедова «Горе от ума». Поэтика заглавия пьесы
Комедия А.С. Грибоедова «Горе от ума». Поэтика заглавия пьесы 1 Приоритетные направления стратегии развития области Модернизация власти, повышение ее конкурентоспособности Развитие человече
1 Приоритетные направления стратегии развития области Модернизация власти, повышение ее конкурентоспособности Развитие человече К. Паустовский Барсучий нос
К. Паустовский Барсучий нос Генетика человека
Генетика человека Maryinsky Park
Maryinsky Park Техническая эксплуатация и обслуживание электрического и электромеханического оборудования
Техническая эксплуатация и обслуживание электрического и электромеханического оборудования Из серии " 100 великих картин "
Из серии " 100 великих картин " Искусство эпохи. Возрождения Проторенессанс. Ранний Ренессанс
Искусство эпохи. Возрождения Проторенессанс. Ранний Ренессанс Простейший ремонт сантехнического оборудования
Простейший ремонт сантехнического оборудования