Слайд 2Начнём по порядку . что же такое стереометрия?
Стереометрия — это раздел геометрии,

в котором изучаются свойства фигур в пространстве.
Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.
Слайд 3Простейшие фигуры в пространстве: точка, прямая, плоскость.
Плоскость.
Представление о плоскости дает
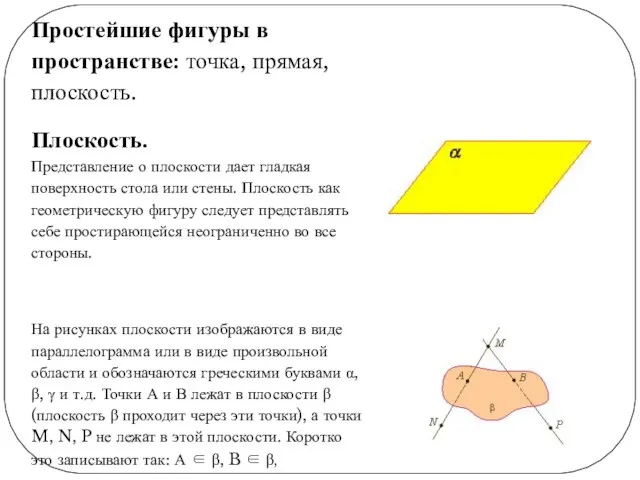
гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,
Слайд 4Аксиомы стереометрии и их следствия , проверим себя . Аксиома 1
Через любые
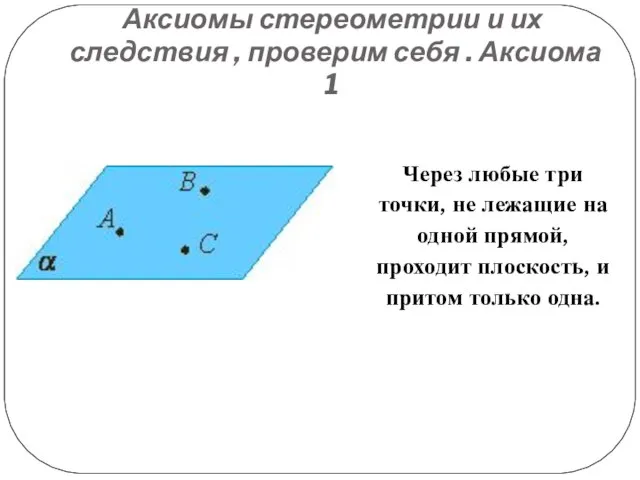
три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Слайд 5Аксиома 2
Если две точки прямой лежат в плоскости, то все точки прямой
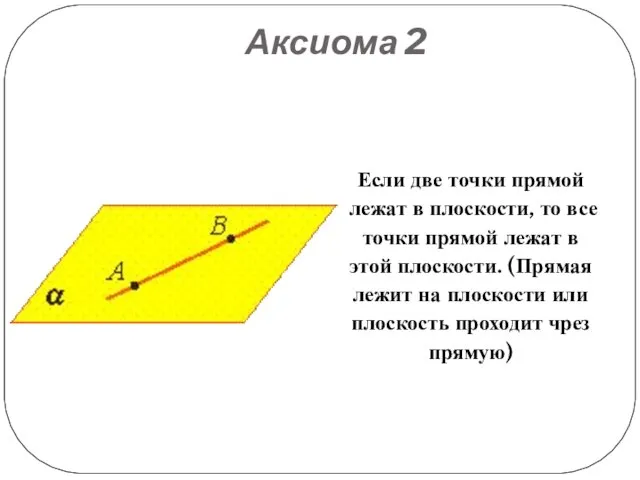
лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит чрез прямую)
Слайд 6Аксиома 3
Если две различные плоскости имеют общую точку, то они имеют общую
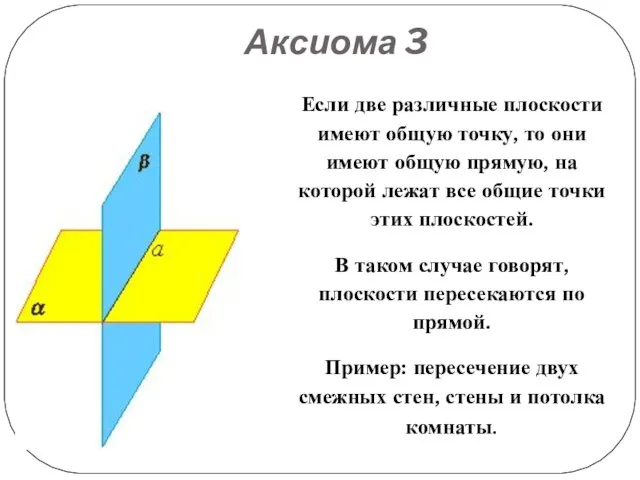
прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты.
Слайд 7Некоторые следствия из аксиом
Теорема 1.
Через прямую a и не лежащую
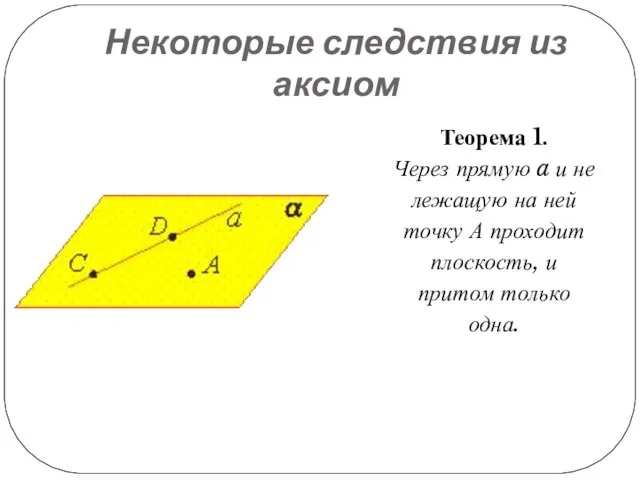
на ней точку А проходит плоскость, и притом только одна.
Слайд 8Из аксиомы 2 следует, что если прямая не лежит в данной плоскости,
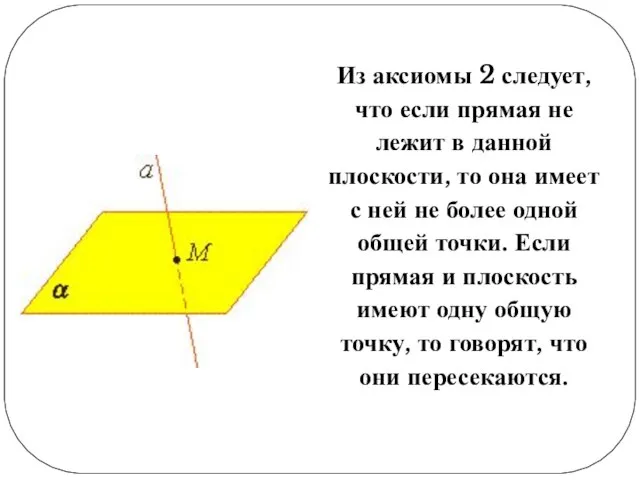
то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Слайд 9Теорема 3.
Через две пересекающиеся прямые a и b проходит плоскость, и
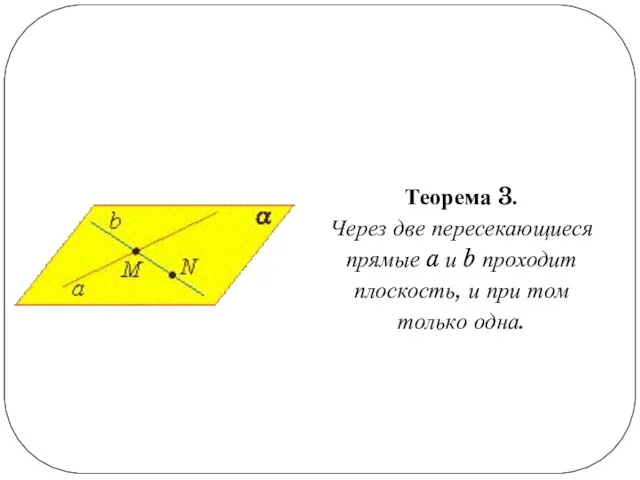
при том только одна.
Слайд 10Параллельные прямые в пространстве .Введём понятие что называют параллельные прямые в пространстве
Две
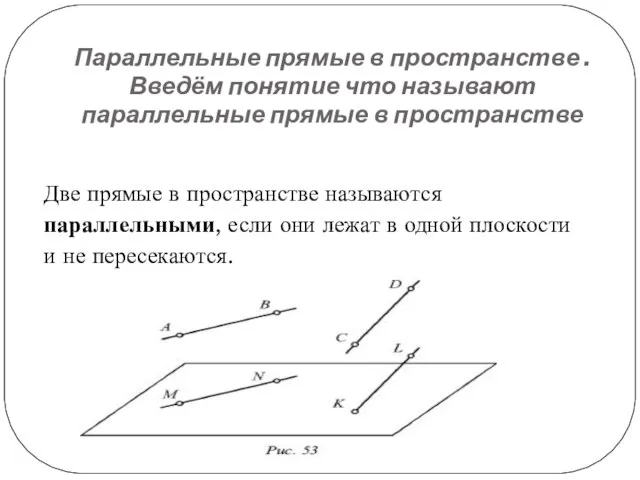
прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Слайд 11Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на данной прямой,
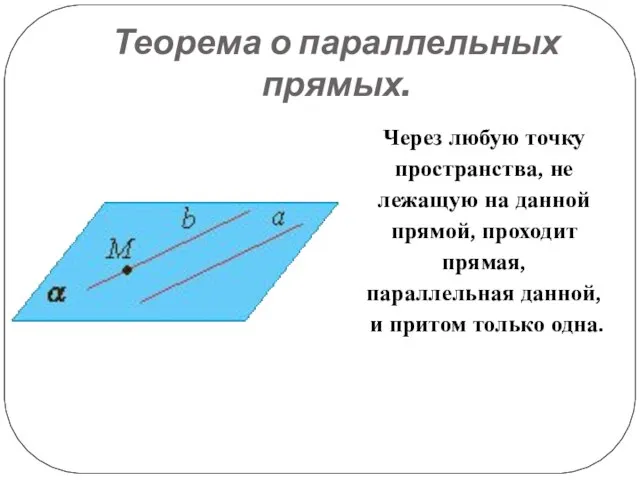
проходит прямая, параллельная данной, и притом только одна.
Слайд 12Лемма о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых
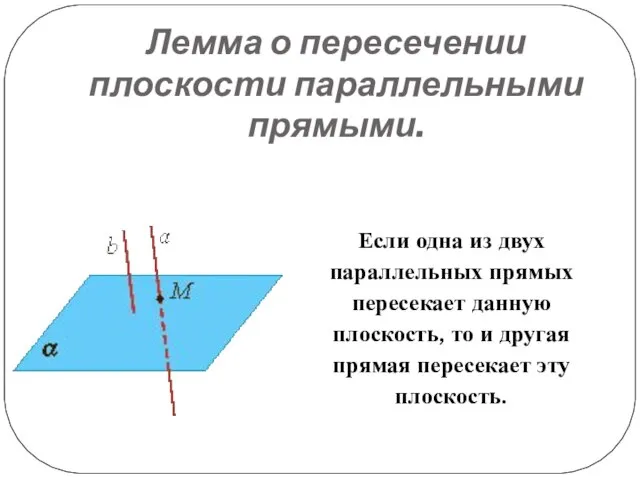
пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Слайд 13Теорема о трех прямых в пространстве.
Если две прямые параллельны третьей прямой, то
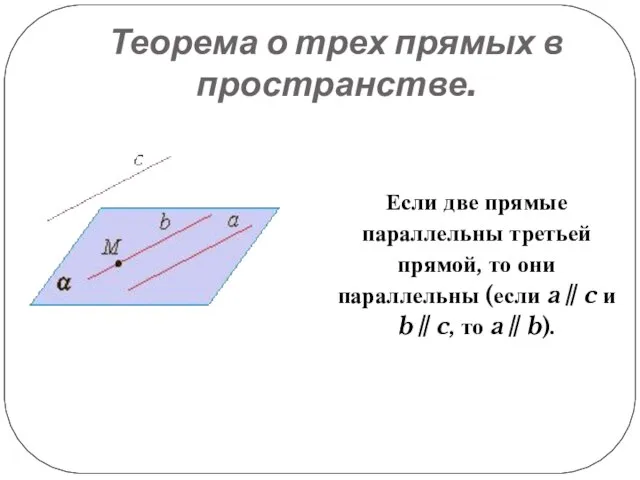
они параллельны (если a∥c и b∥c, то a∥b).












 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр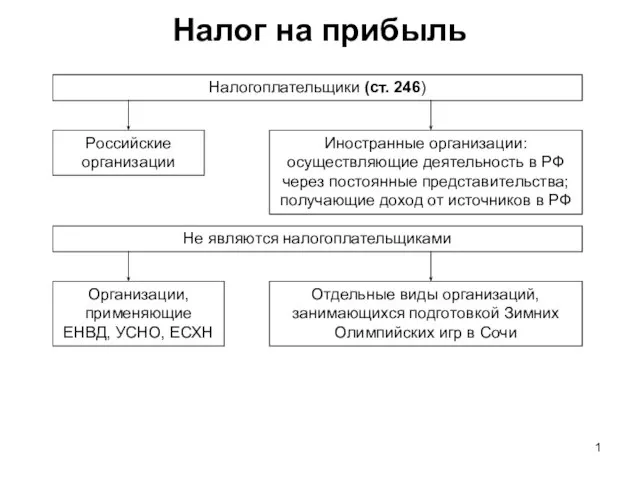 Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология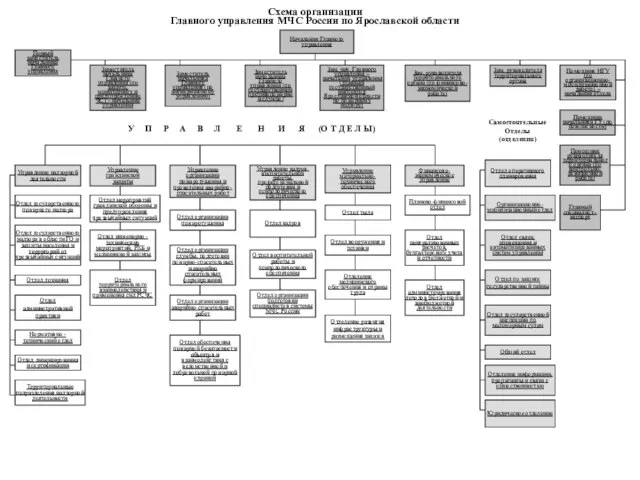 Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва