Параллельность в пространстве

Оглавление
Параллельные прямые в пространстве.
Параллельность трех прямых.
Параллельность прямой и плоскости.
Параллельность плоскостей.
Свойства параллельных плоскостей.
Кроссворд.

Параллельные прямые в пространстве
Определение
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Обозначение
а ιι b
с ιι d

Теорема
Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и причем только одна.
аιιb

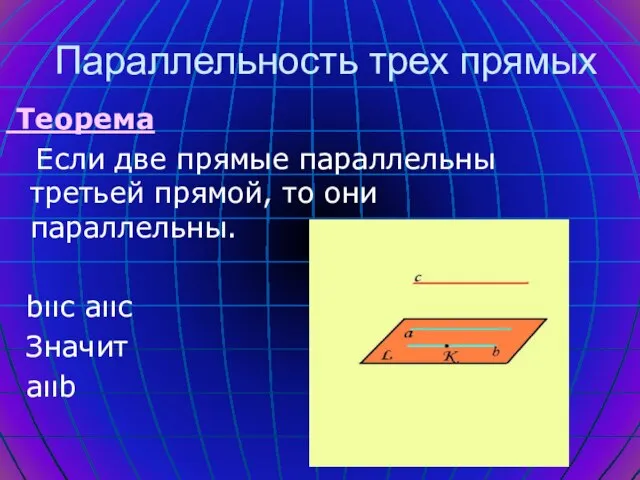
Теорема
Если две прямые параллельны третьей прямой, то они параллельны.
bιιс аιιс
Значит
аιιb
Параллельность трех прямых

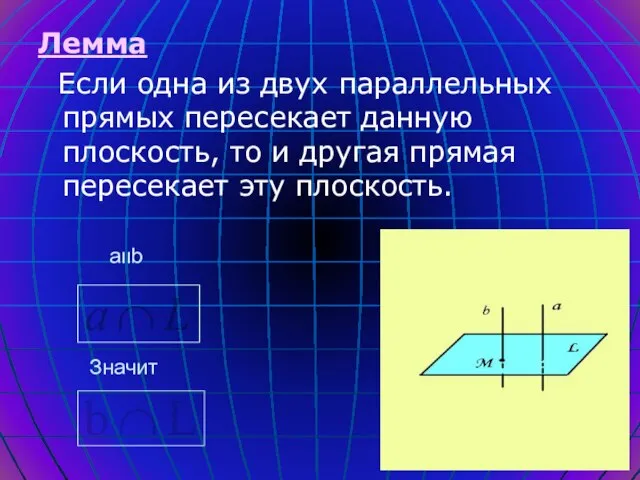
Лемма
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Значит
аιιb

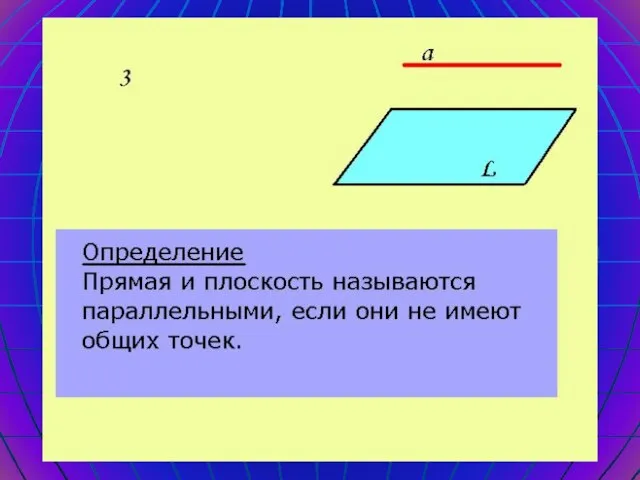
Параллельность прямой и плоскости
Возможны три случая взаимного расположения прямой и плоскости в пространстве:
Прямая лежит в плоскости.
Прямая и плоскость имеют только одну точку.
Прямая и плоскость не имеют общих точек.

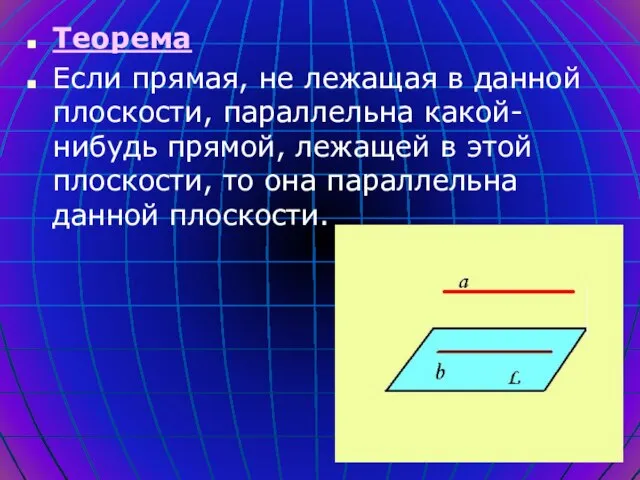
Теорема
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Следствие
Если плоскость проходит через данную прямую параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Следствие
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Параллельность плоскостей

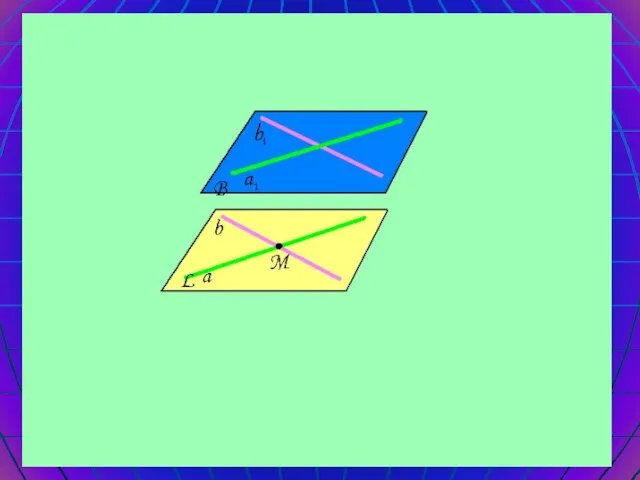
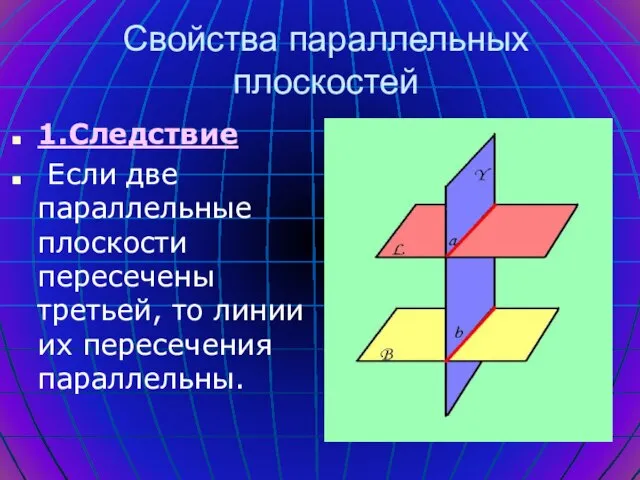
Свойства параллельных плоскостей
1.Следствие
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

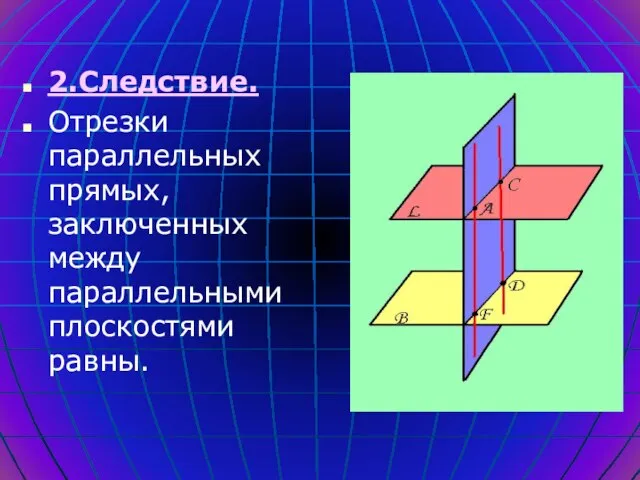
2.Следствие.
Отрезки параллельных прямых, заключенных между параллельными плоскостями равны.