Содержание
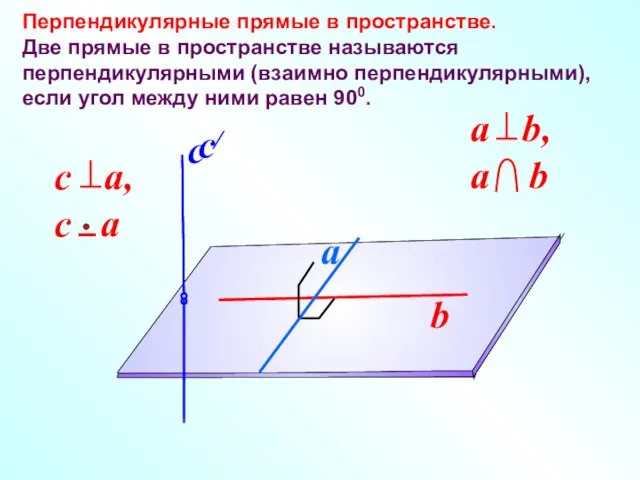
- 2. Перпендикулярные прямые в пространстве. Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними
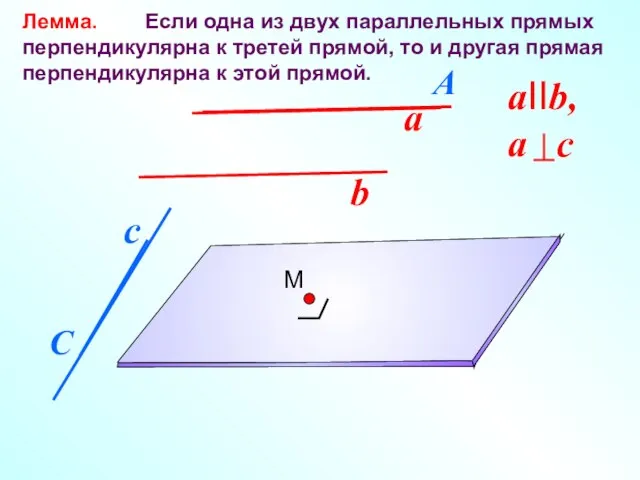
- 3. Лемма. Если одна из двух параллельных прямых перпендикулярна к третей прямой, то и другая прямая перпендикулярна
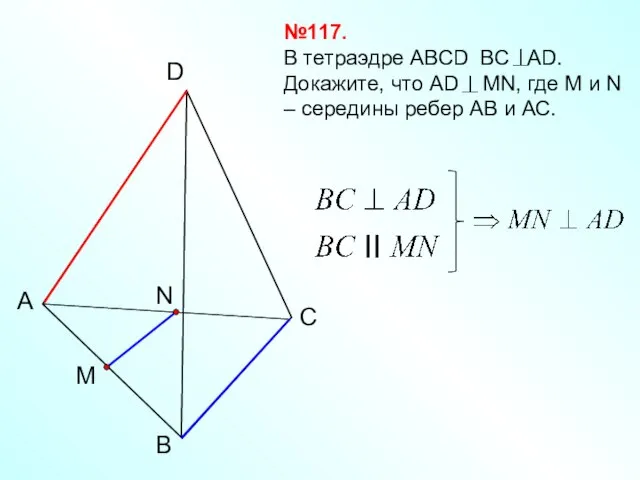
- 4. B А C D №117. В тетраэдре АВСD ВС АD. Докажите, что АD MN, где М
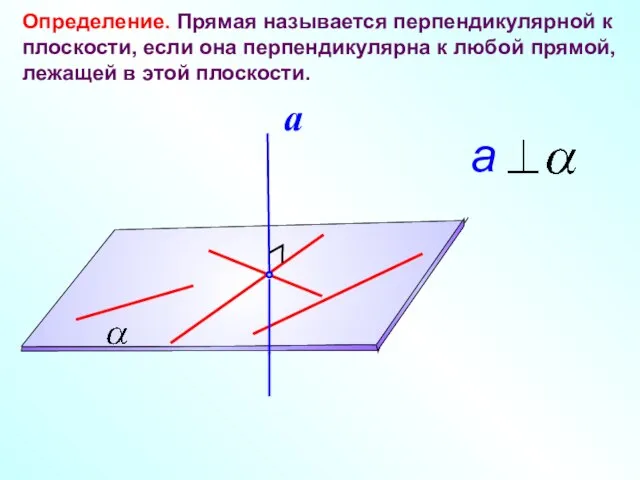
- 5. Определение. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
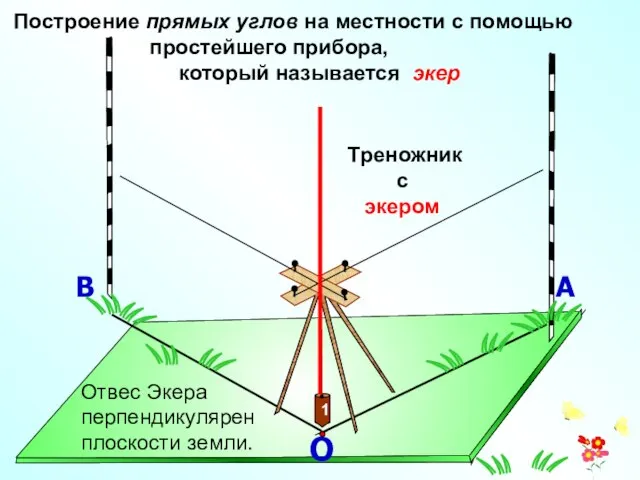
- 6. О А В Построение прямых углов на местности с помощью простейшего прибора, который называется экер Треножник
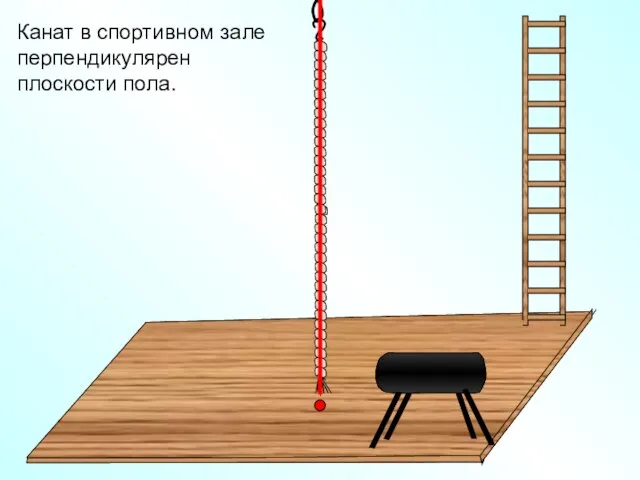
- 7. Канат в спортивном зале перпендикулярен плоскости пола.
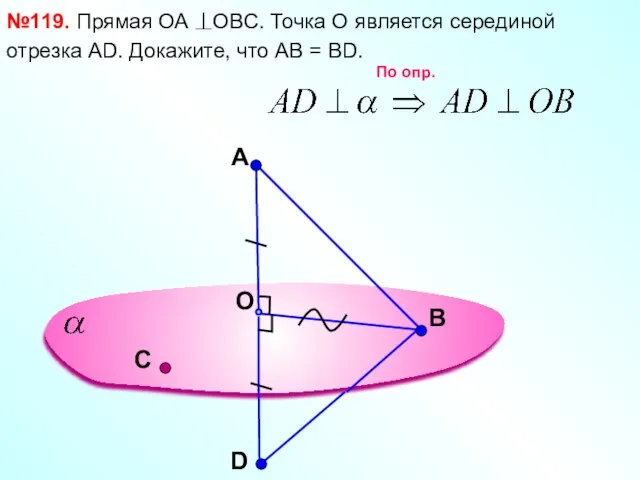
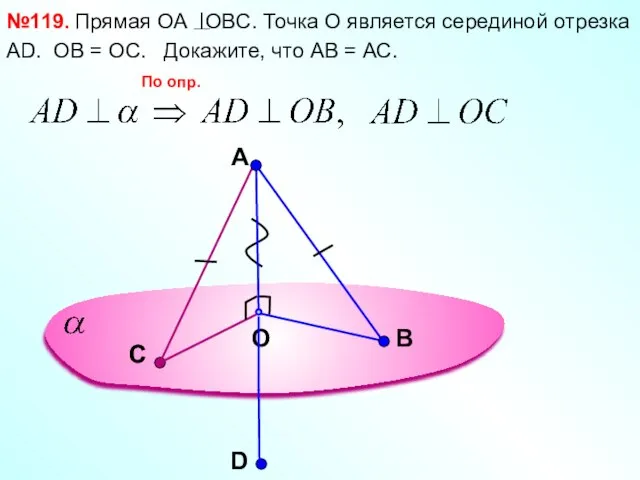
- 9. A O В №119. Прямая ОА OBC. Точка О является серединой отрезка АD. Докажите, что АВ
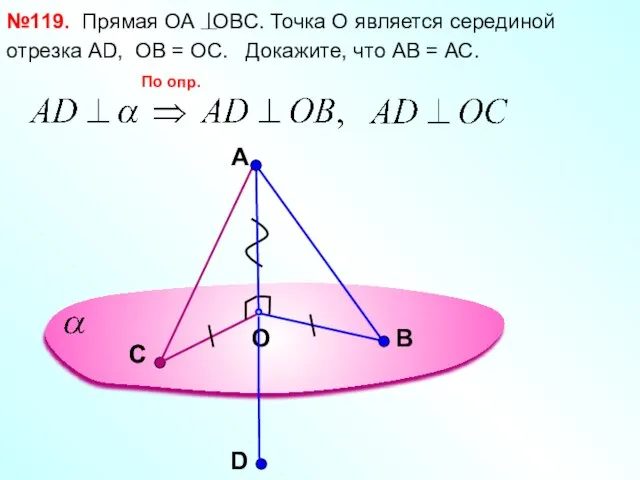
- 10. A O В №119. Прямая ОА OBC. Точка О является серединой отрезка АD, ОВ = ОС.
- 11. A O В №119. Прямая ОА OBC. Точка О является серединой отрезка АD. ОВ = ОС.
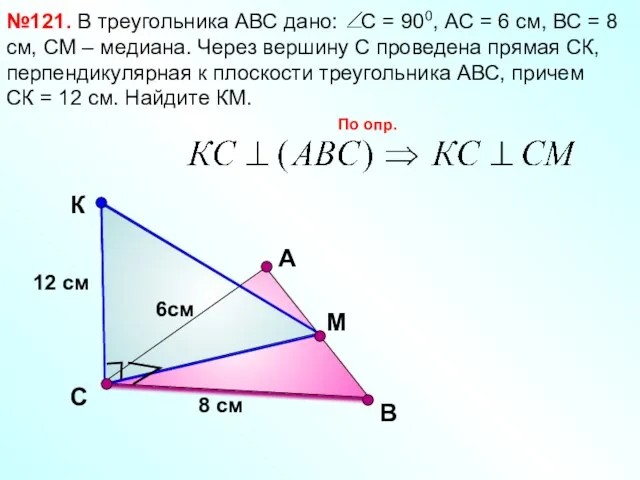
- 12. В №121. В треугольника АВС дано: С = 900, АС = 6 см, ВС = 8
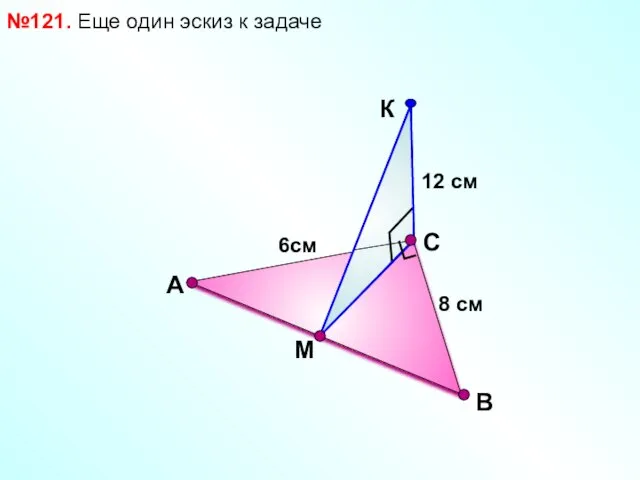
- 13. В №121. Еще один эскиз к задаче С А М 12 см 8 см 6см
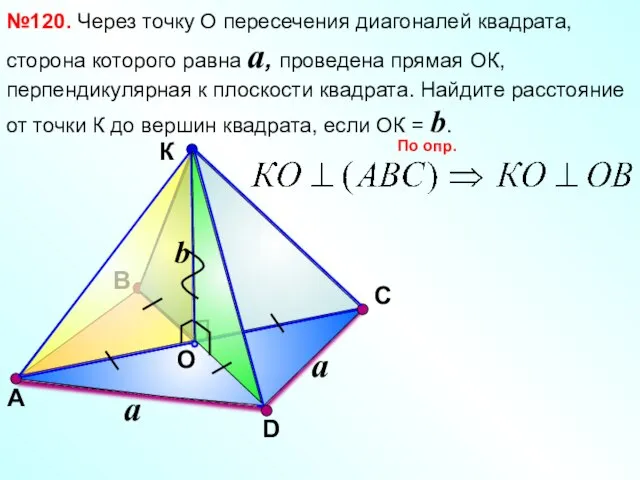
- 14. В К O С №120. Через точку О пересечения диагоналей квадрата, сторона которого равна a, проведена
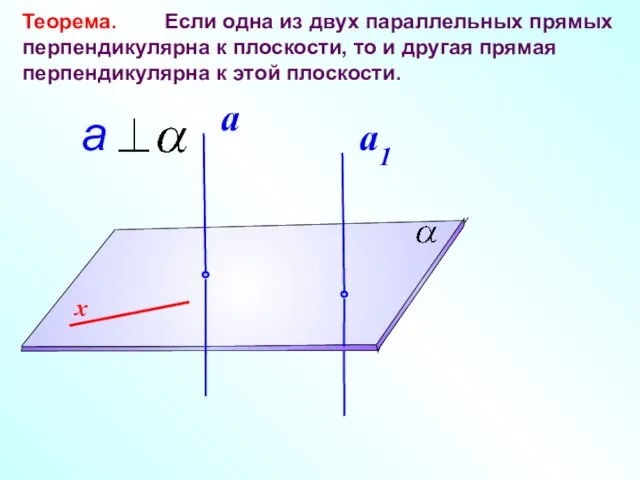
- 15. Теорема. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к
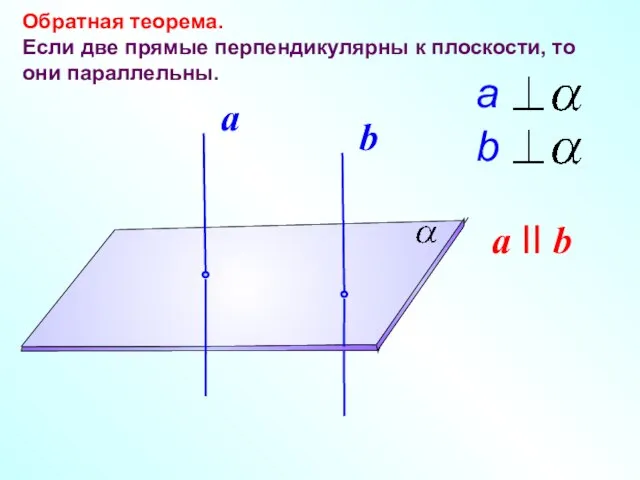
- 16. Обратная теорема. Если две прямые перпендикулярны к плоскости, то они параллельны. a II b
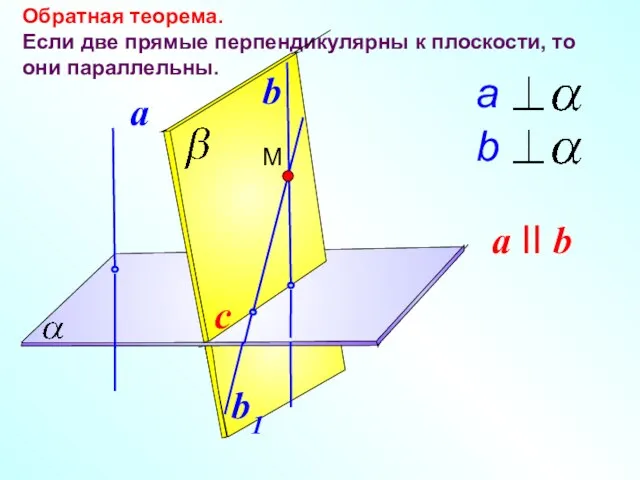
- 17. Обратная теорема. Если две прямые перпендикулярны к плоскости, то они параллельны. a II b c
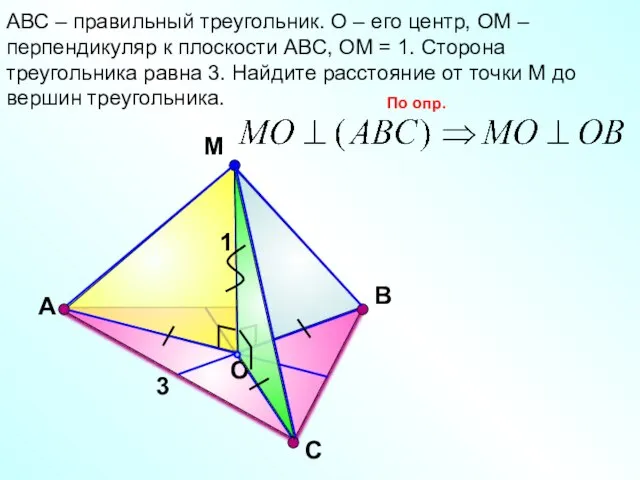
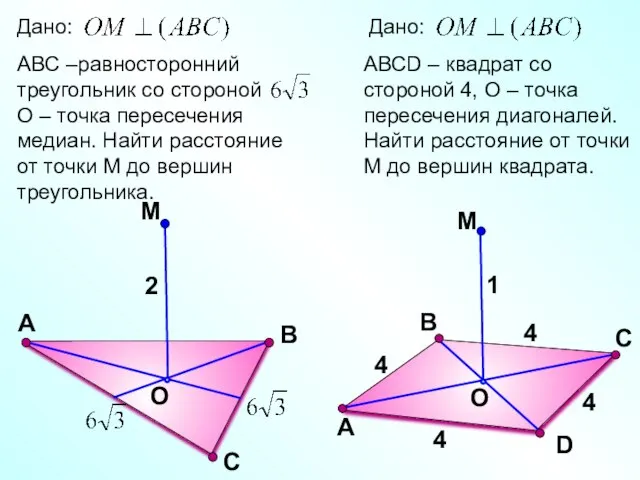
- 18. С М O В АВС – правильный треугольник. О – его центр, ОМ – перпендикуляр к
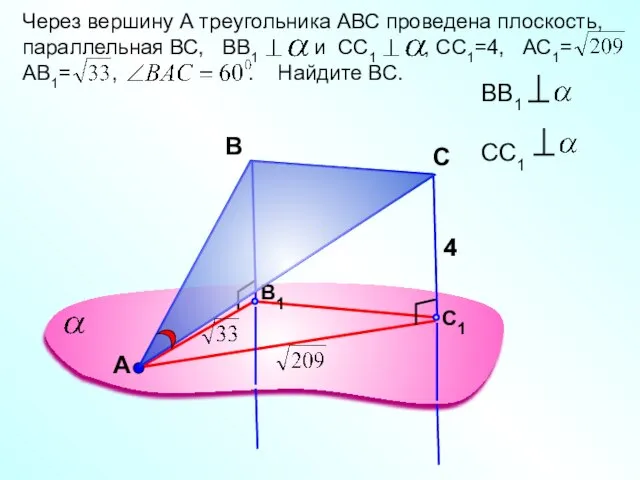
- 19. А Через вершину А треугольника АВС проведена плоскость, параллельная ВС, ВВ1 и СС1 , СС1=4, АС1=
- 20. С М O В А 2 D В М O С А АВСD – квадрат со
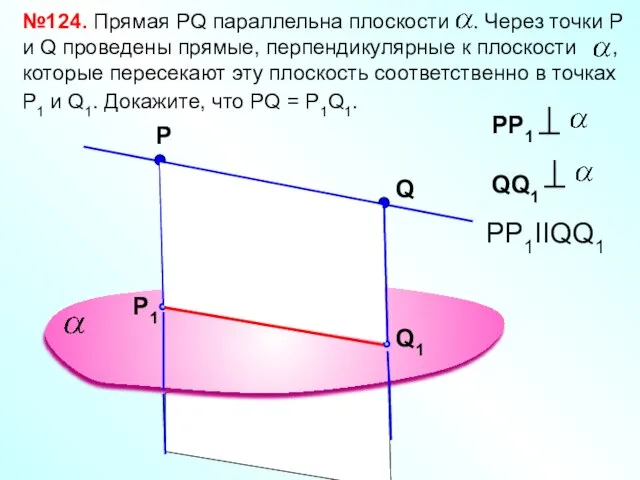
- 21. Р №124. Прямая РQ параллельна плоскости . Через точки Р и Q проведены прямые, перпендикулярные к
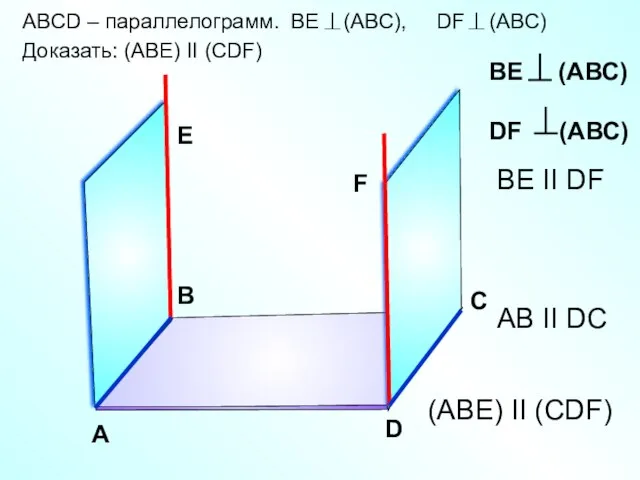
- 22. ABCD – параллелограмм. BE (ABC), DF (ABC) Доказать: (АВЕ) II (СDF) А В С D ВЕ
- 24. Скачать презентацию

 Студенческий научный кружок кафедры фармакогнозии с курсом ботаники
Студенческий научный кружок кафедры фармакогнозии с курсом ботаники Психология личности преступника
Психология личности преступника Презентация на тему: Последовательное и параллельное соединение проводников
Презентация на тему: Последовательное и параллельное соединение проводников Вальс
Вальс Jagermeister. Дегустация в Виталюр
Jagermeister. Дегустация в Виталюр Презентация на тему Радиационный фон школьных помещений
Презентация на тему Радиационный фон школьных помещений  КАК ЗАЩИТИТЬСЯ
КАК ЗАЩИТИТЬСЯ КТО? ЧТО? ГДЕ? КОГДА? КТО? ООО «Деловая Россия» и Интернет-компания «АПСЕЛФ» приглашает талантливых креативных людей к участию в отк
КТО? ЧТО? ГДЕ? КОГДА? КТО? ООО «Деловая Россия» и Интернет-компания «АПСЕЛФ» приглашает талантливых креативных людей к участию в отк Организация образовательного процесса в инклюзивном детском саду
Организация образовательного процесса в инклюзивном детском саду ABM Art-Business-Moda. Показ одежды
ABM Art-Business-Moda. Показ одежды Образ Санкт-Петербурга в произведениях Достоевского
Образ Санкт-Петербурга в произведениях Достоевского Конституция Республики Татарстан
Конституция Республики Татарстан Презентация на тему Мое педагогическое кредо
Презентация на тему Мое педагогическое кредо Теория оптимальной фильтрации и управления
Теория оптимальной фильтрации и управления Сочинение по роману в стихах «Евгений Онегин» А. С. Пушкина
Сочинение по роману в стихах «Евгений Онегин» А. С. Пушкина СОВРЕМЕННОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕДЛЯ РОССИЙСКОЙ ИННОВАЦИОННОЙ СИСТЕМЫВ ОБЛАСТИ ЭЛЕКТРОНИКИ
СОВРЕМЕННОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕДЛЯ РОССИЙСКОЙ ИННОВАЦИОННОЙ СИСТЕМЫВ ОБЛАСТИ ЭЛЕКТРОНИКИ ДИПЛОМНАЯ РАБОТАФерменты и механизмы регуляции ферментативной активности в организме
ДИПЛОМНАЯ РАБОТАФерменты и механизмы регуляции ферментативной активности в организме CIVIL LAW Tort Law
CIVIL LAW Tort Law ГОТОВИМСЯ К ЕГЭ
ГОТОВИМСЯ К ЕГЭ Простые числа
Простые числа Вкусные числа
Вкусные числа Северный Инвестиционный Банк:Финансирование энергосберегающих проектов в России
Северный Инвестиционный Банк:Финансирование энергосберегающих проектов в России Аквалія Термаль Річ. Насичений крем для глибокого зволоження шкіри обличчя
Аквалія Термаль Річ. Насичений крем для глибокого зволоження шкіри обличчя Звук и буква «Ш»
Звук и буква «Ш» Правовые основы финансов. Финансовое право. Бюджетный и налоговый кодексы
Правовые основы финансов. Финансовое право. Бюджетный и налоговый кодексы Нулевая декларация в Латвии
Нулевая декларация в Латвии Реализация требований закона №152-ФЗ при развертывании системы защиты персональных данныхв отдельно взятом муниципальном обра
Реализация требований закона №152-ФЗ при развертывании системы защиты персональных данныхв отдельно взятом муниципальном обра Продукты Gyproc
Продукты Gyproc