Перспектива

Лекция 1. ПЕРСПЕКТИВА.
Перспектива точки, прямой линии
ОБЩИЕ СВЕДЕНИЯ
Перспективой (перспективной проекцией) называется центральная проекция предмета на специально выбранную поверхность.
Перспектива происходит от латинского глагола "perspicere" − видеть насквозь.
Перспектива является одним из методов построения наглядных изображений пространственных предметов, которые широко используются в инженерной графике и особенно в архитектурно-строительном черчении.

В зависимости от вида поверхности, на которой строятся перспективные проекции, различают следующие виды перспективы:
Линейная перспектива − проецирование на вертикальную плоскость.
Плафонная перспектива − проецирование на горизонтальную плоскость.
Панорамная перспектива − проецирование на цилиндрическую поверхность.
Купольная перспектива − проецирование на сферу.

ЛИНЕЙНАЯ ПЕРСПЕКТИВА
Ограничимся рассмотрением только линейной перспективы, т.е. рассмотрением центрального проецирования на вертикальную плоскость.
Построение перспективы предмета из некоторой точки (точки зрения) осуществляется в следующей последовательности:
1. Из точки проводим лучи ко всем точкам предмета.
2. На пути проецирующих лучей располагаем плоскость.
3. Точки пересечения лучей с плоскостью определяют искомое изображение.

ОСНОВНЫЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
Горизонтальная плоскость П1 проекций, на которой располагается объект проецирования (здание, сооружение), называется предметной плоскостью. Перпендикулярная ей плоскость, на которую осуществляется перспективное проецирование, называется картинной плоскостью или картиной и обозначается К.
Центр проецирования S, т.е. точка, в которой располагается глаз наблюдателя, называется точкой зрения.

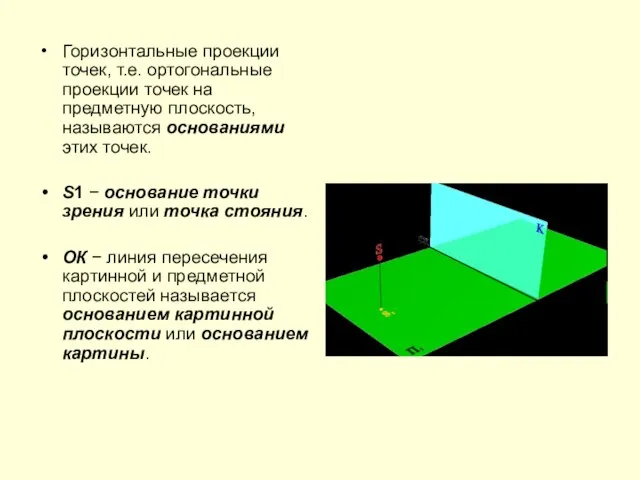
Горизонтальные проекции точек, т.е. ортогональные проекции точек на предметную плоскость, называются основаниями этих точек.
S1 − основание точки зрения или точка стояния.
ОК − линия пересечения картинной и предметной плоскостей называется основанием картинной плоскости или основанием картины.

Горизонтальная плоскость, проходящая через точку зрения S, называется плоскостью горизонта.
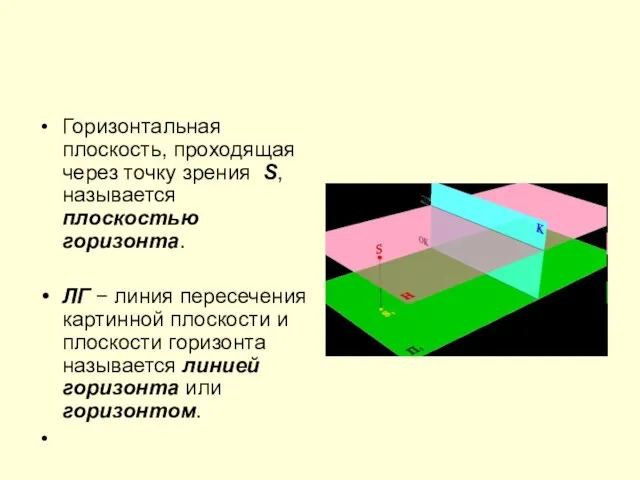
ЛГ − линия пересечения картинной плоскости и плоскости горизонта называется линией горизонта или горизонтом.

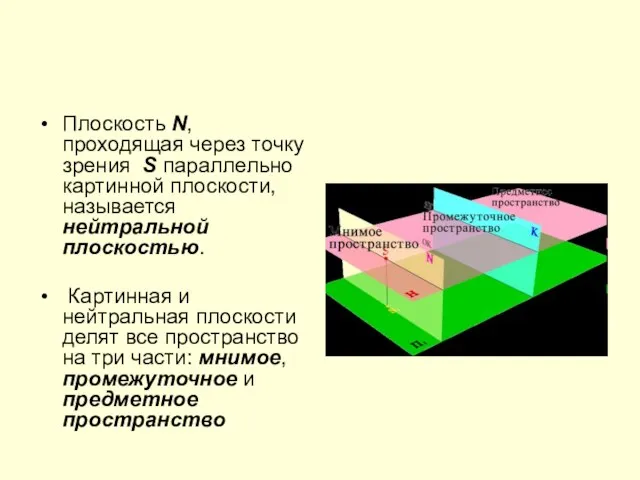
Плоскость N, проходящая через точку зрения S параллельно картинной плоскости, называется нейтральной плоскостью.
Картинная и нейтральная плоскости делят все пространство на три части: мнимое, промежуточное и предметное пространство

Перпендикуляр, восстановленный из точки зрения S на картинную плоскость, называется главным лучом.
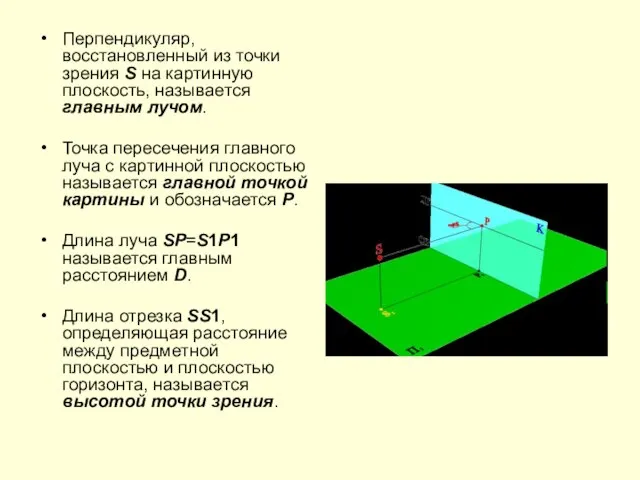
Точка пересечения главного луча с картинной плоскостью называется главной точкой картины и обозначается Р.
Длина луча SP=S1P1 называется главным расстоянием D.
Длина отрезка SS1, определяющая расстояние между предметной плоскостью и плоскостью горизонта, называется высотой точки зрения.

ПЕРСПЕКТИВА ТОЧКИ
Чтобы построить перспективу точки А, расположенной в предметном пространстве, необходимо из точки S провести проецирующий луч через точку А. Точка пересечения этого проецирующего луча [SA) с картинной плоскостью К определит перспективу точки А − А'.
Аналогично можно найти перспективу основания точки А − A1'. Точка A1' называется перспективой основания точки А или вторичной перспективной проекцией точки А (первичной проекцией считается ортогональная проекция точки А1).

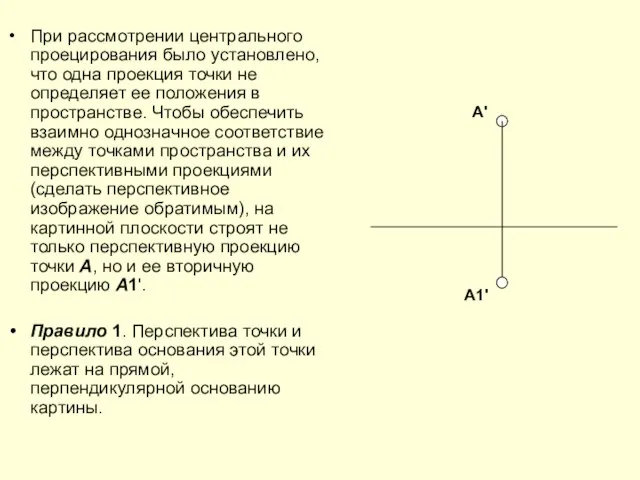
При рассмотрении центрального проецирования было установлено, что одна проекция точки не определяет ее положения в пространстве. Чтобы обеспечить взаимно однозначное соответствие между точками пространства и их перспективными проекциями (сделать перспективное изображение обратимым), на картинной плоскости строят не только перспективную проекцию точки А, но и ее вторичную проекцию A1'.
Правило 1. Перспектива точки и перспектива основания этой точки лежат на прямой, перпендикулярной основанию картины.

ПЕРСПЕКТИВА ПРЯМЫХ ОБЩЕГО ПОЛОЖЕНИЯ
На основании свойств центрального проецирования можно сформулировать следующие правила перспективных проекций прямых общего положения:
Правило 2. Перспектива прямой есть прямая.

Правило 3.
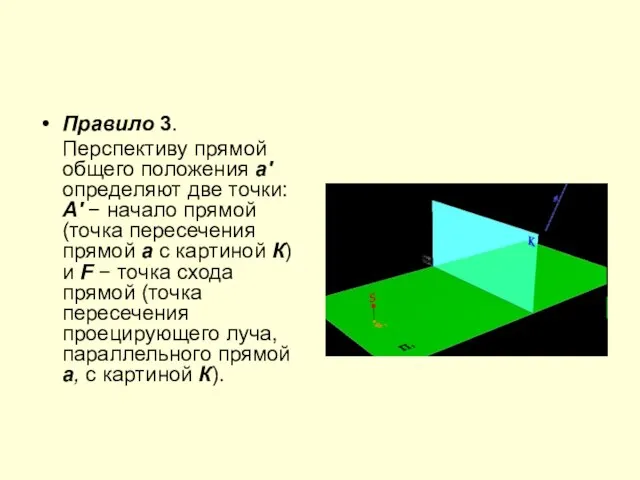
Перспективу прямой общего положения a' определяют две точки: А' − начало прямой (точка пересечения прямой a с картиной К) и F − точка схода прямой (точка пересечения проецирующего луча, параллельного прямой a, с картиной К).

Правило 4.
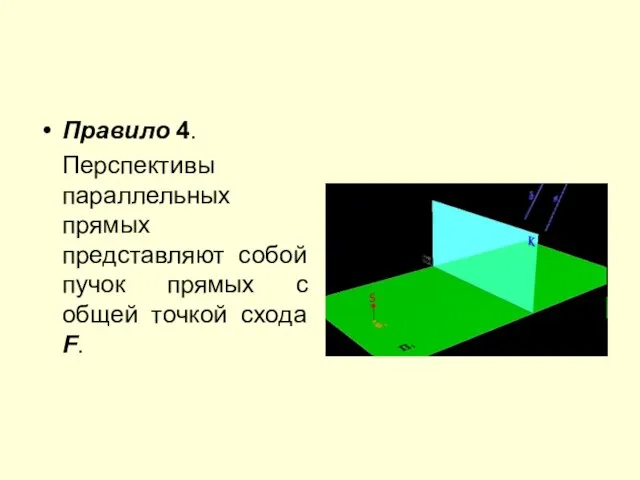
Перспективы параллельных прямых представляют собой пучок прямых с общей точкой схода F.

ПЕРСПЕКТИВЫ ГОРИЗОНТАЛЬНЫХ ПРЯМЫХ
Горизонтальные прямые произвольного положения относительно картины
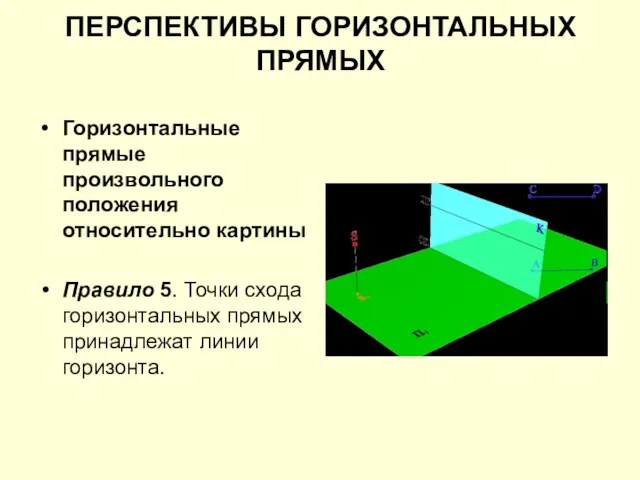
Правило 5. Точки схода горизонтальных прямых принадлежат линии горизонта.

Горизонтальные прямые, расположенные под углом 45° к картине
Правило 6.
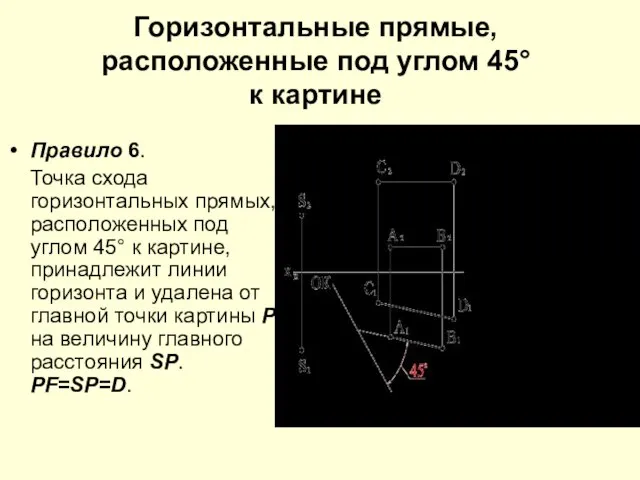
Точка схода горизонтальных прямых, расположенных под углом 45° к картине, принадлежит линии горизонта и удалена от главной точки картины Р на величину главного расстояния SP. PF=SP=D.

Горизонтальные прямые, перпендикулярные картине
Правило 7.
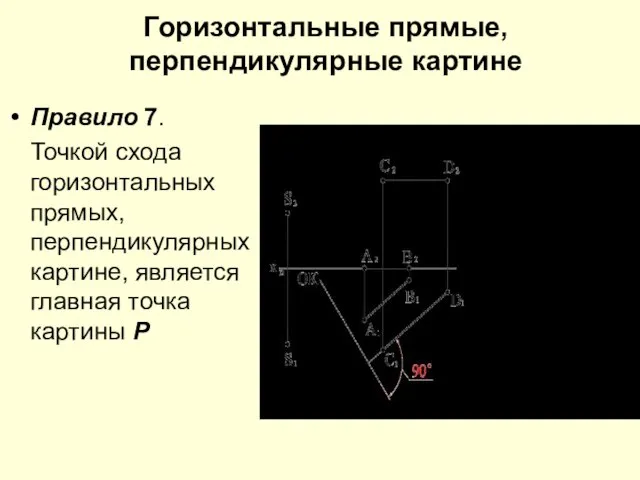
Точкой схода горизонтальных прямых, перпендикулярных картине, является главная точка картины Р

Горизонтальные прямые, проходящие через основание точки зрения
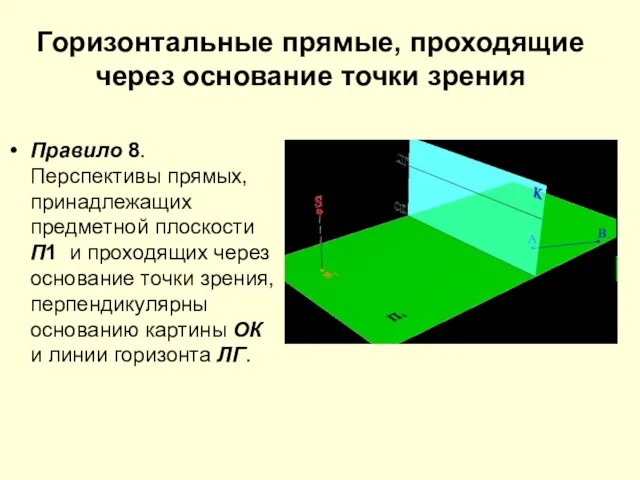
Правило 8. Перспективы прямых, принадлежащих предметной плоскости П1 и проходящих через основание точки зрения, перпендикулярны основанию картины ОК и линии горизонта ЛГ.

ПЕРСПЕКТИВА ВЕРТИКАЛЬНОГО ОТРЕЗКА
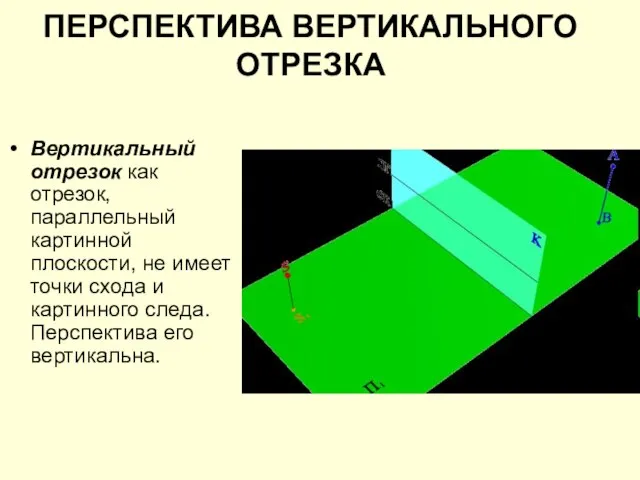
Вертикальный отрезок как отрезок, параллельный картинной плоскости, не имеет точки схода и картинного следа. Перспектива его вертикальна.

ПОСТРОЕНИЕ ПЕРСПЕКТИВЫ ТОЧКИ
Точку в перспективе можно получить как результат пересечения двух прямых, для построения перспективы которых широко применяется метод построения с использованием точек схода параллельных прямых.
Построение перспективы можно выполнять с использованием одной или двух точек схода.