Построение сечений многогранников

Содержание
Определение.
Примеры построений сечений.
Задания на построение сечений.

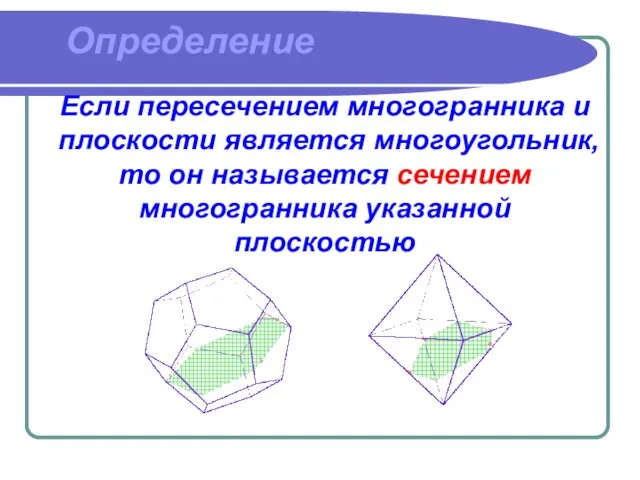
Определение
Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника указанной плоскостью

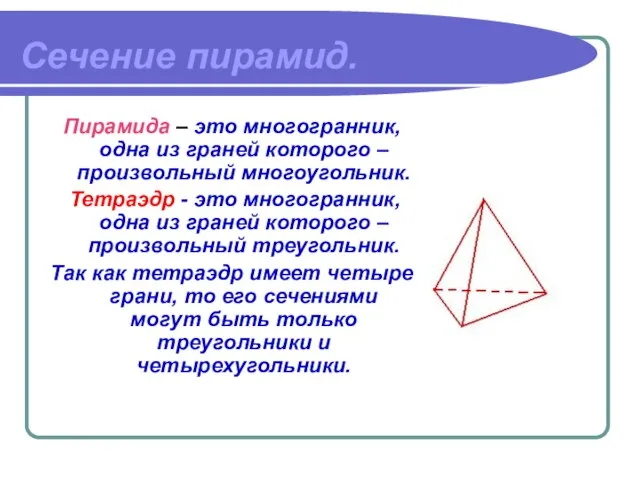
Сечение пирамид.
Пирамида – это многогранник, одна из граней которого – произвольный многоугольник. Тетраэдр - это многогранник, одна из граней которого – произвольный треугольник.
Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырехугольники.

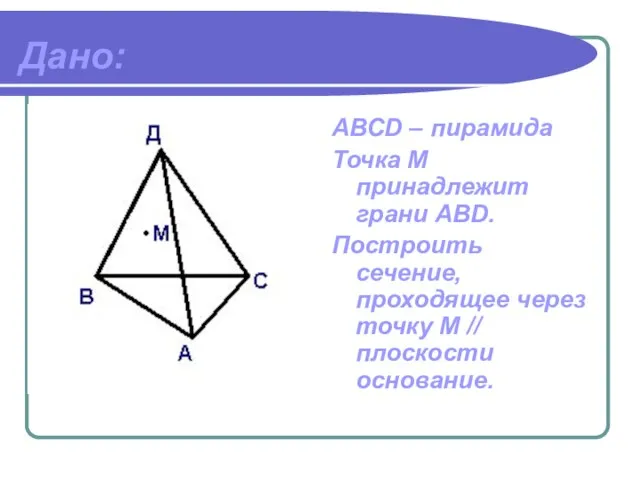
Дано:
АВСD – пирамида
Точка М принадлежит грани ABD.
Построить сечение, проходящее через точку М // плоскости основание.

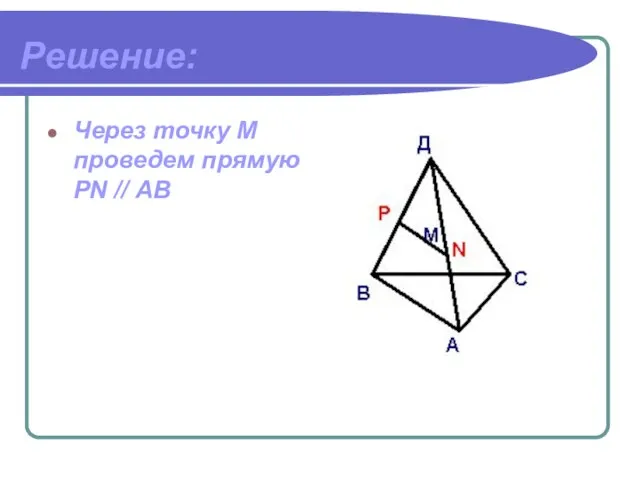
Решение:
Через точку М проведем прямую PN // АВ

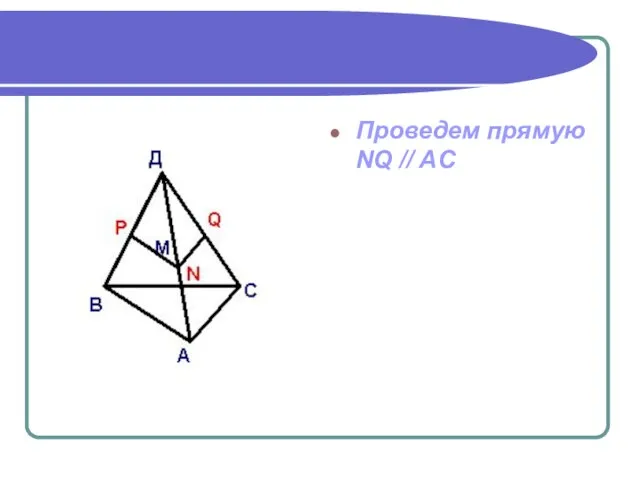
Проведем прямую NQ // AC

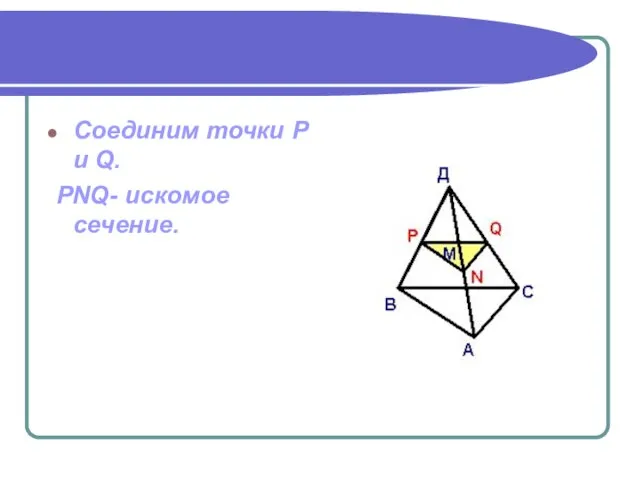
Соединим точки P и Q.
PNQ- искомое сечение.

Дано:
Пирамида MABCD. Постройте сечение пирамиды, проходящее через точки P, Q, R. Известно, что точка P ∈ MB, точка R ∈ MA, Q ∈DC.
ВАЖНО!
Если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам.

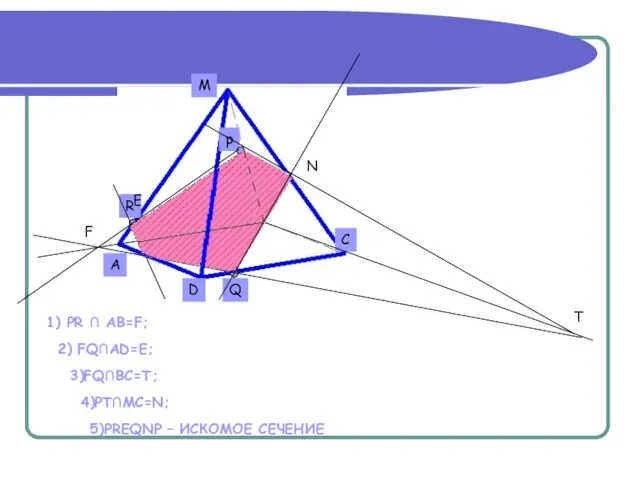
F
T
1) PR ∩ AB=F;
2) FQ∩AD=E;
3)FQ∩BC=T;
4)PT∩MC=N;
5)PREQNP – ИСКОМОЕ СЕЧЕНИЕ
Е
N

Сечение куба
Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.
Куб имеет 6 граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.

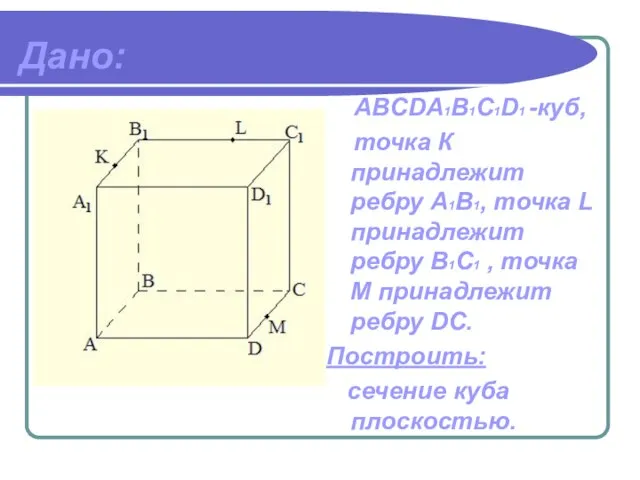
Дано:
ABCDА1B1C1D1 -куб,
точка К принадлежит ребру A1В1, точка L принадлежит ребру В1C1 , точка М принадлежит ребру DC.
Построить:
сечение куба плоскостью.

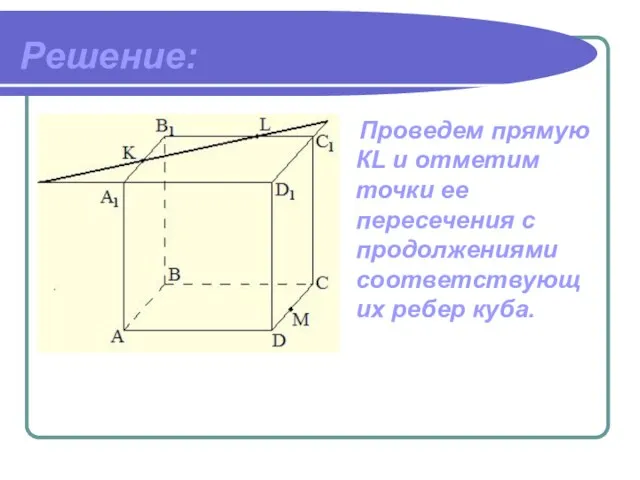
Решение:
Проведем прямую КL и отметим точки ее пересечения с продолжениями соответствующих ребер куба.

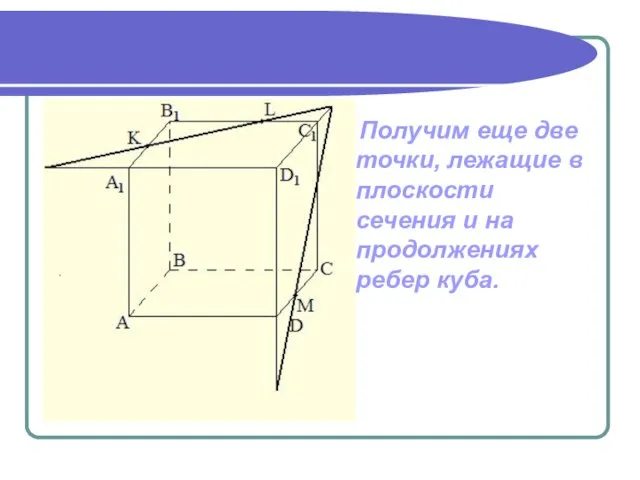
Получим еще две точки, лежащие в плоскости сечения и на продолжениях ребер куба.

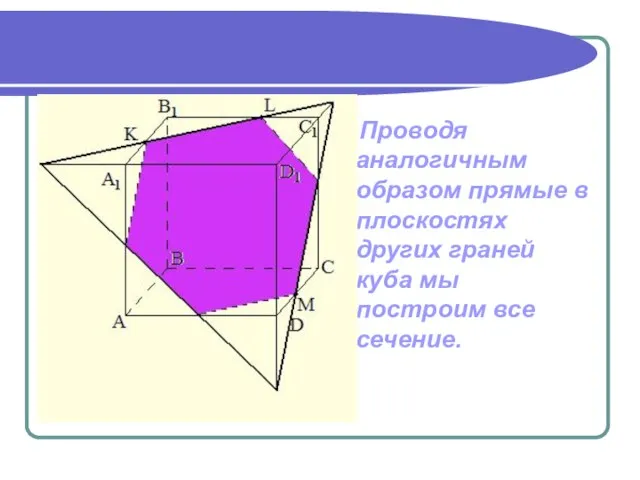
Проводя аналогичным образом прямые в плоскостях других граней куба мы построим все сечение.

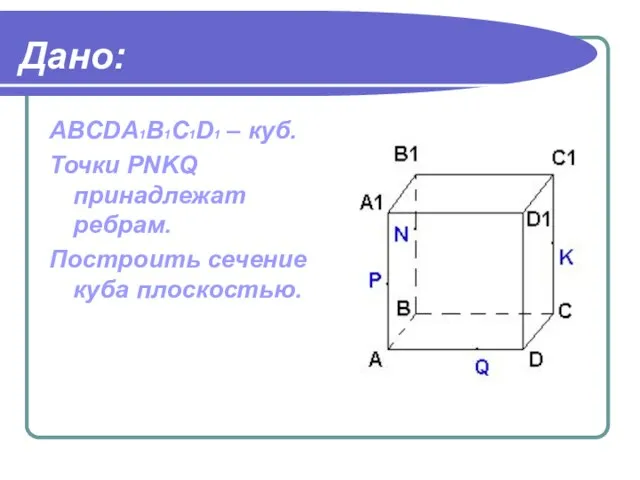
Дано:
ABCDA1B1C1D1 – куб.
Точки PNKQ принадлежат ребрам.
Построить сечение куба плоскостью.

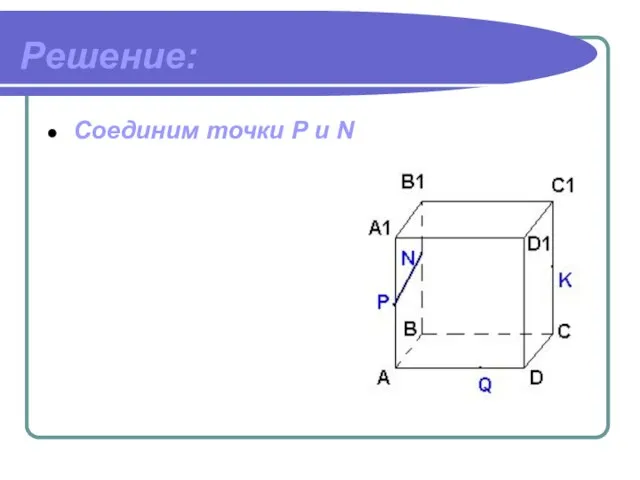
Решение:
Соединим точки P и N

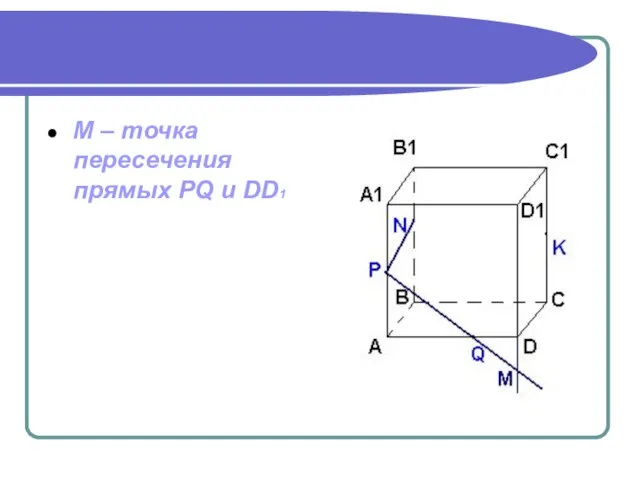
М – точка пересечения прямых PQ и DD1

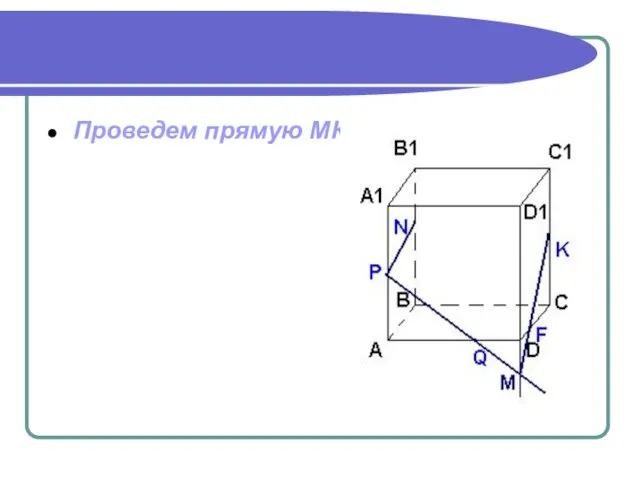
Проведем прямую МК

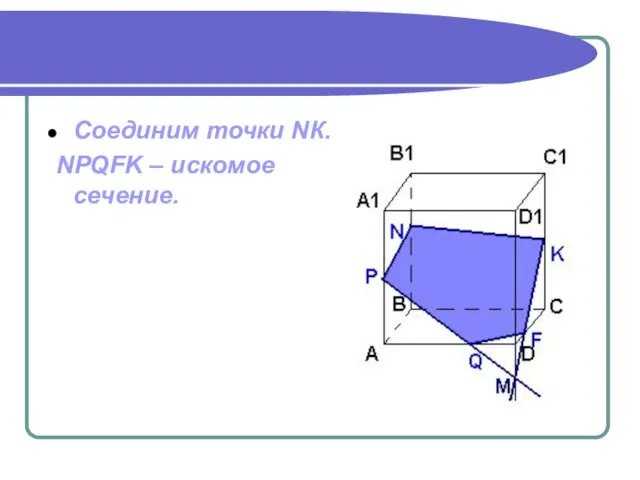
Соединим точки NК.
NPQFK – искомое сечение.

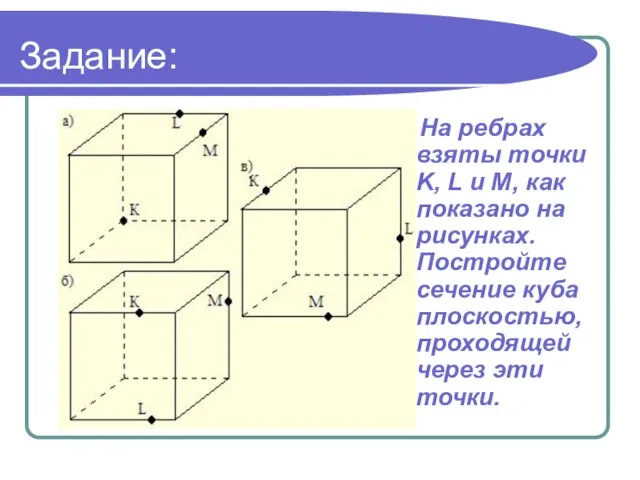
Задание:
На ребрах взяты точки K, L и M, как показано на рисунках. Постройте сечение куба плоскостью, проходящей через эти точки.

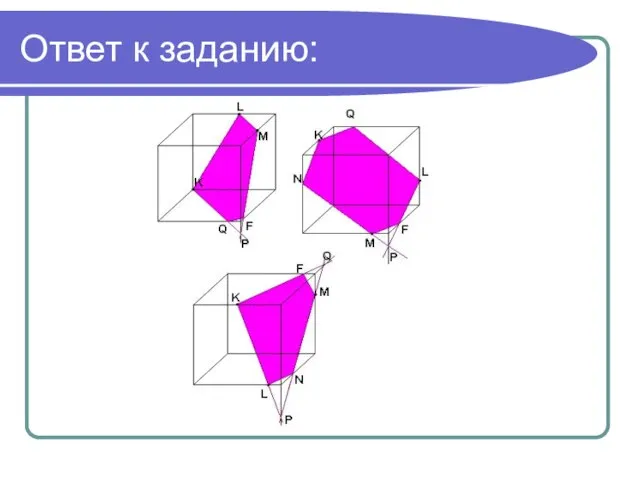
Ответ к заданию:

Мир многогранников!

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук» Л.Кэрролл

За каждым многогранником закреплено его значение, НАПРИМЕР:
Тетраэдр является огнём!

куб-земля

октаэдр-воздух

Даже пчёлы знакомы с понятием многогранник!!!