Построение сечения геометрических тел плоскостью

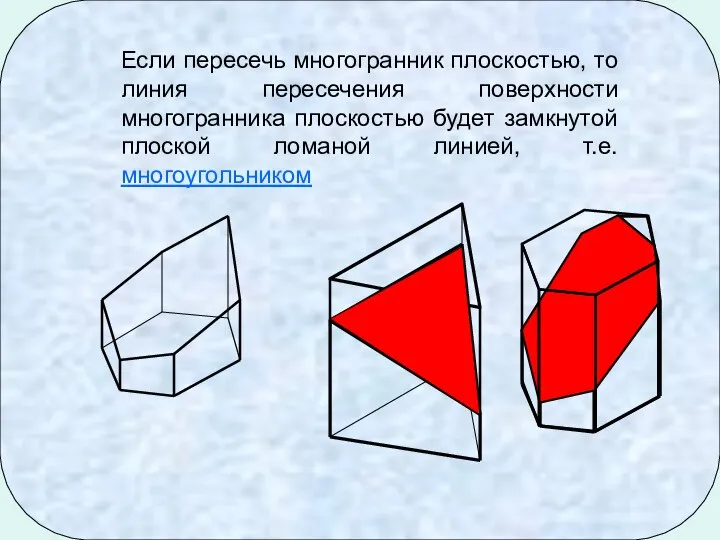
Если пересечь многогранник плоскостью, то линия пересечения поверхности многогранника плоскостью будет замкнутой плоской ломаной линией, т.е. многоугольником

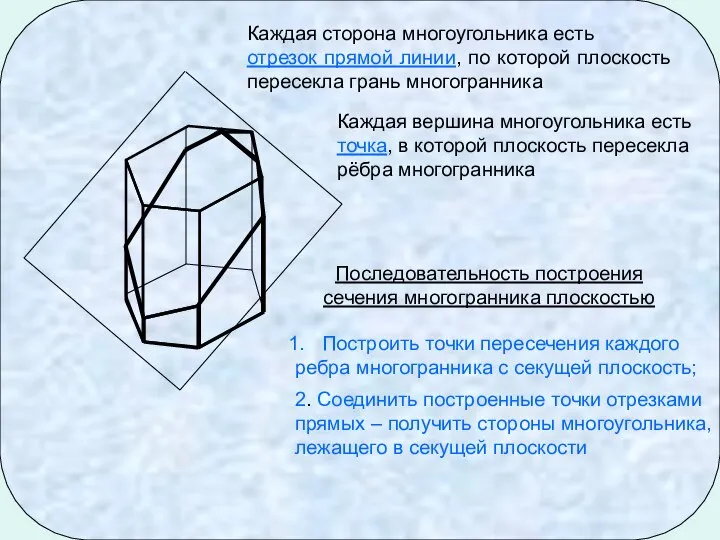
Каждая сторона многоугольника есть
отрезок прямой линии, по которой плоскость пересекла грань многогранника
Каждая вершина многоугольника есть
точка, в которой плоскость пересекла
рёбра многогранника
Последовательность построения
сечения многогранника плоскостью
Построить точки пересечения каждого
ребра многогранника с секущей плоскость;
2. Соединить построенные точки отрезками
прямых – получить стороны многоугольника,
лежащего в секущей плоскости

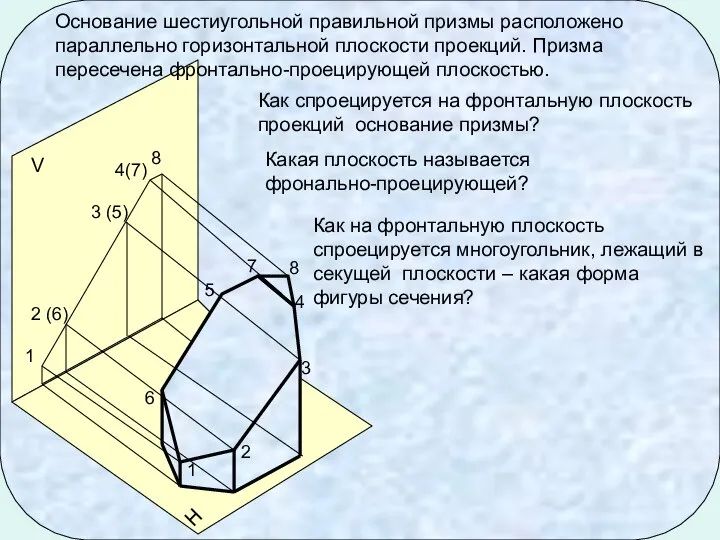
7
1
2
3
4
5
6
H
V
8
Основание шестиугольной правильной призмы расположено параллельно горизонтальной плоскости проекций. Призма пересечена фронтально-проецирующей плоскостью.
Как спроецируется на фронтальную плоскость
проекций основание призмы?
Какая плоскость называется
фронально-проецирующей?
Как на фронтальную плоскость
спроецируется многоугольник, лежащий в
секущей плоскости – какая форма фигуры сечения?
1
2 (6)
3 (5)
4(7)
8

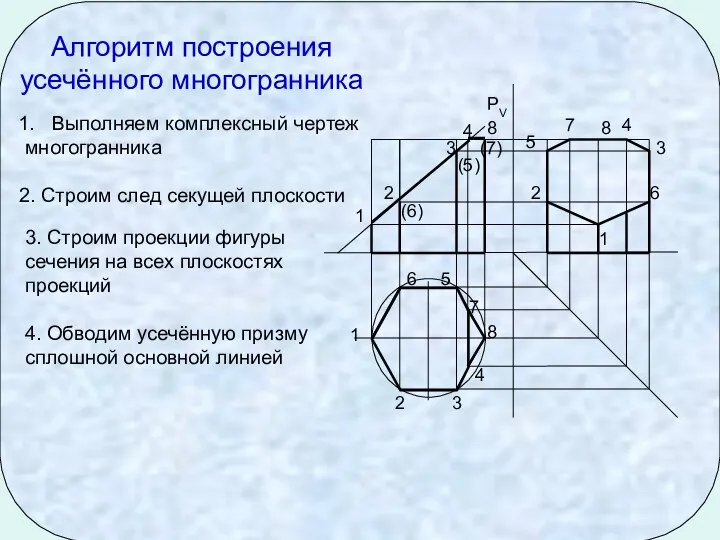
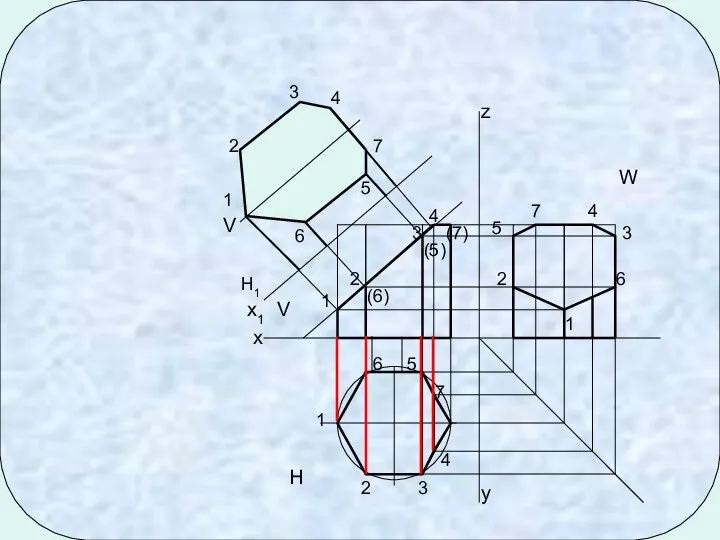
1
2
3
4
5
(6)
1
2
3
3
2
4
4
5
(5)
6
6
1
(7)
7
7
8
8
8
Алгоритм построения
усечённого многогранника
PV
Выполняем комплексный чертеж
многогранника
2. Строим след секущей плоскости
3. Строим проекции фигуры
сечения на всех плоскостях
проекций
4. Обводим усечённую призму
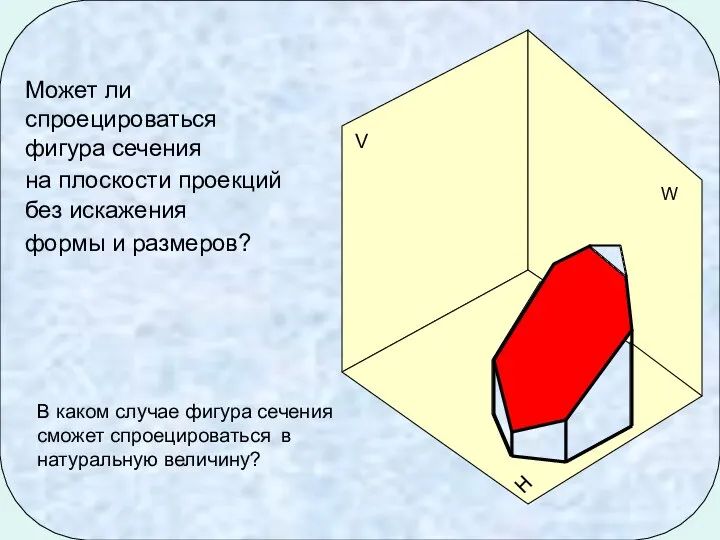
сплошной основной линией

Может ли спроецироваться
фигура сечения
на плоскости проекций
без искажения
формы и размеров?
В каком случае фигура сечения
сможет спроецироваться в
натуральную величину?

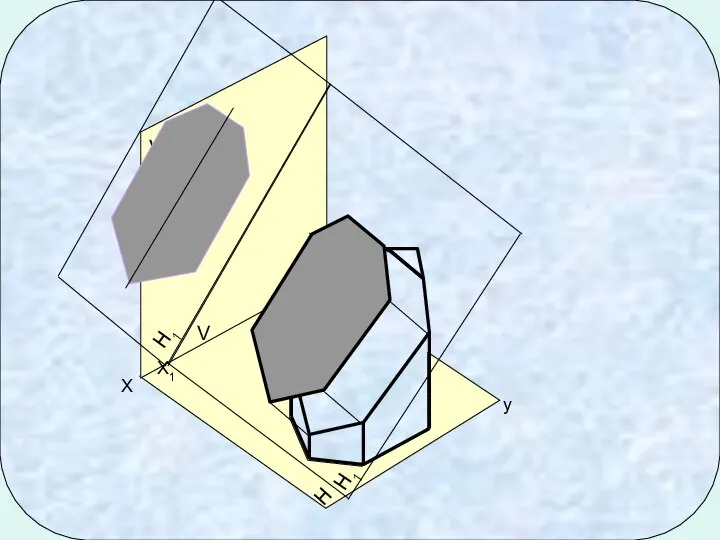
Нахождение натуральной величины сечения способом перемены плоскостей проекций

H
V
X
X1
y
V
H1
H1

1
2
3
4
5
(6)
1
2
3
3
2
4
4
5
(5)
6
6
1
(7)
7
7
H
V
W
x1
y
x
H1
V
z
1
2
3
4
6
7
5

Самостоятельная работа студентов