Предельные деформации бетона перед разрушением

Предельная сжимаемость εbu и предельная растяжимость εbt,u зависят от прочности бетона, его класса, длительности приложения нагрузки.
С увеличением класса бетона предельные деформации уменьшаются, а с ростом длительности приложения нагрузки – увеличиваются.
Предельные деформации бетона перед разрушением
116

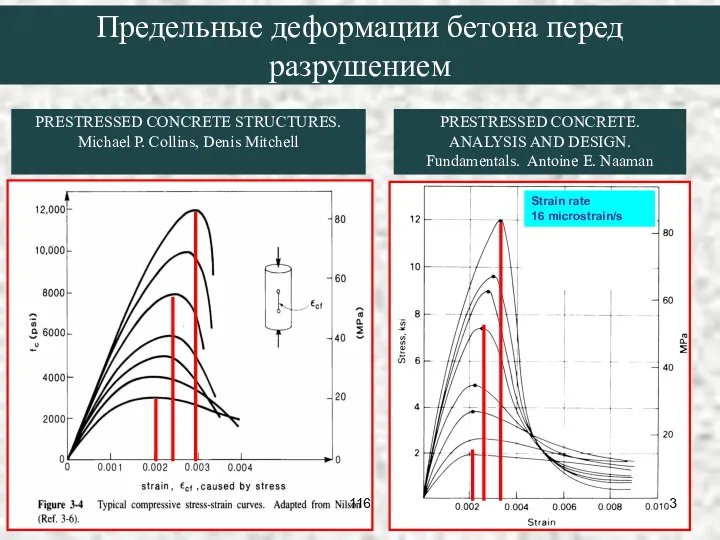
PRESTRESSED CONCRETE STRUCTURES.
Michael P. Collins, Denis Mitchell
PRESTRESSED CONCRETE. ANALYSIS AND DESIGN. Fundamentals. Antoine E. Naaman
Strain rate
16 microstrain/s
Предельные деформации бетона перед разрушением
116

;
;
.
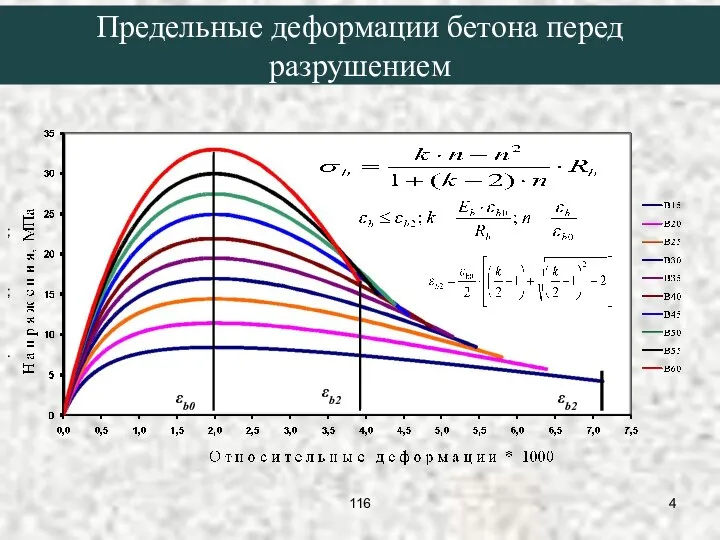
εb2
εb0
εb2
Предельные деформации бетона перед разрушением
116

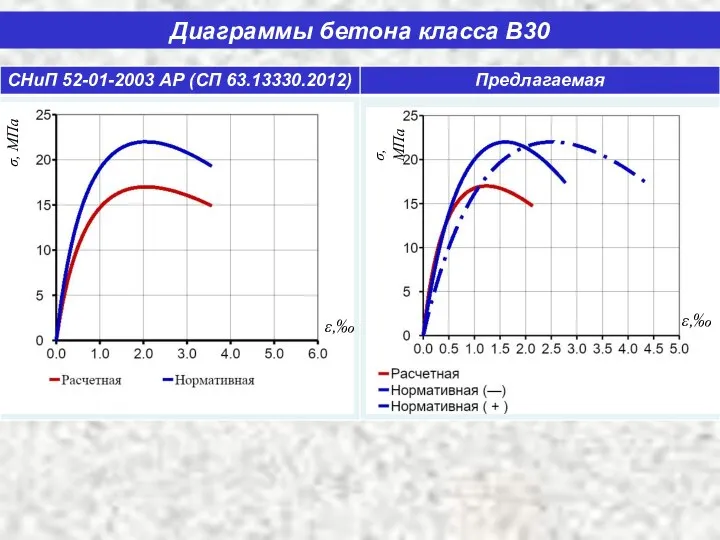
Диаграммы бетона класса В30
σ, МПа
σ, МПа
ε,‰
ε,‰

При центральном сжатии бетонных призм εbu=(0,8…3,0)⋅10-3, в среднем ее принимают εbu=2,0⋅10-3.
Предельные деформации бетона перед разрушением
116

При центральном сжатии бетонных призм εbu=(0,8…3,0)⋅10-3, в среднем ее принимают εbu=2,0⋅10-3.
В сжатой зоне изгибаемых элементов наблюдается большая, чем у сжатых призм, предельная сжимаемость, зависящая от формы поперечного сечения εbu=(2,7…4,5)⋅10-3:
Предельные деформации бетона перед разрушением
116

При центральном сжатии бетонных призм εbu=(0,8…3,0)⋅10-3, в среднем ее принимают εbu=2,0⋅10-3.
В сжатой зоне изгибаемых элементов наблюдается большая, чем у сжатых призм, предельная сжимаемость, зависящая от формы поперечного сечения εbu=(2,7…4,5)⋅10-3:
Предельная растяжимость бетона в 10…20 раз меньше, чем предельная сжимаемость εbt,u=1,5⋅10-4.
Предельные деформации бетона перед разрушением
116

При центральном сжатии бетонных призм εbu=(0,8…3,0)⋅10-3, в среднем ее принимают εbu=2,0⋅10-3.
В сжатой зоне изгибаемых элементов наблюдается большая, чем у сжатых призм, предельная сжимаемость, зависящая от формы поперечного сечения εbu=(2,7…4,5)⋅10-3:
Предельная растяжимость бетона в 10…20 раз меньше, чем предельная сжимаемость εbt,u=1,5⋅10-4.
У бетонов на пористых заполнителях предельная сжимаемость и растяжимость ≈ в 2 раза выше, чем у тяжелых бетонов.
Предельные деформации бетона перед разрушением
116

При центральном сжатии бетонных призм εbu=(0,8…3,0)⋅10-3, в среднем ее принимают εbu=2,0⋅10-3.
В сжатой зоне изгибаемых элементов наблюдается большая, чем у сжатых призм, предельная сжимаемость, зависящая от формы поперечного сечения εbu=(2,7…4,5)⋅10-3:
Предельная растяжимость бетона в 10…20 раз меньше, чем предельная сжимаемость εbt,u=1,5⋅10-4.
У бетонов на пористых заполнителях предельная сжимаемость и растяжимость ≈ в 2 раза выше, чем у тяжелых бетонов.
Коэффициент поперечных деформаций:
Предельные деформации бетона перед разрушением
116

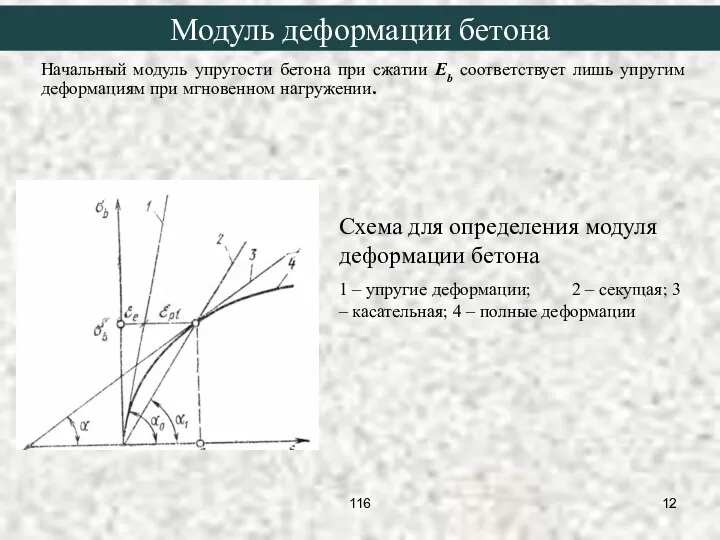
Начальный модуль упругости бетона при сжатии Eb соответствует лишь упругим деформациям при мгновенном нагружении.
Модуль деформации бетона
116

Начальный модуль упругости бетона при сжатии Eb соответствует лишь упругим деформациям при мгновенном нагружении.
Схема для определения модуля деформации бетона
1 – упругие деформации; 2 – секущая; 3 – касательная; 4 – полные деформации
Модуль деформации бетона
116

Начальный модуль упругости бетона при сжатии Eb соответствует лишь упругим деформациям при мгновенном нагружении.
Геометрическая интерпретация:
Схема для определения модуля деформации бетона
1 – упругие деформации; 2 – секущая; 3 – касательная; 4 – полные деформации
Модуль деформации бетона
116

Начальный модуль упругости бетона при сжатии Eb соответствует лишь упругим деформациям при мгновенном нагружении.
Геометрическая интерпретация:
Модуль полных деформаций бетона при сжатии Eb соответствует полным деформациям (включая ползучесть) является переменной величиной; геометрически он определяется как тангенс угла наклона касательной к кривой σb - εb в точке с заданным напряжением:
Схема для определения модуля деформации бетона
1 – упругие деформации; 2 – секущая; 3 – касательная; 4 – полные деформации
Модуль деформации бетона
116

Начальный модуль упругости бетона при сжатии Eb соответствует лишь упругим деформациям при мгновенном нагружении.
Геометрическая интерпретация:
Модуль полных деформаций бетона при сжатии Eb соответствует полным деформациям (включая ползучесть) является переменной величиной; геометрически он определяется как тангенс угла наклона касательной к кривой σb - εb в точке с заданным напряжением:
Для расчета используют модуль упругопластичности бетона (тангенс угла наклона секущей в точке на кривой σb - εb с заданным напряжением):
Схема для определения модуля деформации бетона
1 – упругие деформации; 2 – секущая; 3 – касательная; 4 – полные деформации
Модуль деформации бетона
116

Начальный модуль упругости бетона при сжатии Eb соответствует лишь упругим деформациям при мгновенном нагружении.
Геометрическая интерпретация:
Модуль полных деформаций бетона при сжатии Eb соответствует полным деформациям (включая ползучесть) является переменной величиной; геометрически он определяется как тангенс угла наклона касательной к кривой σb - εb в точке с заданным напряжением:
Для расчета используют модуль упругопластичности бетона (тангенс угла наклона секущей в точке на кривой σb - εb с заданным напряжением):
Так как угол α1 меняется в зависимости от напряжений и времени, модуль упругопластичности также является переменной величиной, меньше, чем начальный модуль упругости.
Схема для определения модуля деформации бетона
1 – упругие деформации; 2 – секущая; 3 – касательная; 4 – полные деформации
Модуль деформации бетона
116

Геометрическая интерпретация:
Модуль полных деформаций бетона при сжатии Eb соответствует полным деформациям (включая ползучесть) является переменной величиной; геометрически он определяется как тангенс угла наклона касательной к кривой σb - εb в точке с заданным напряжением:
Для расчета используют модуль упругопластичности бетона (тангенс угла наклона секущей в точке на кривой σb - εb с заданным напряжением):
Так как угол α1 меняется в зависимости от напряжений и времени, модуль упругопластичности также является переменной величиной, меньше, чем начальный модуль упругости.
Модуль деформации бетона
116

Геометрическая интерпретация:
Модуль полных деформаций бетона при сжатии Eb соответствует полным деформациям (включая ползучесть) является переменной величиной; геометрически он определяется как тангенс угла наклона касательной к кривой σb - εb в точке с заданным напряжением:
Для расчета используют модуль упругопластичности бетона (тангенс угла наклона секущей в точке на кривой σb - εb с заданным напряжением):
Так как угол α1 меняется в зависимости от напряжений и времени, модуль упругопластичности также является переменной величиной, меньше, чем начальный модуль упругости.
Коэффициент νb меняется от 1 (при упругой работе) до 0,15.
Модуль деформации бетона
116

Геометрическая интерпретация:
Модуль полных деформаций бетона при сжатии Eb соответствует полным деформациям (включая ползучесть) является переменной величиной; геометрически он определяется как тангенс угла наклона касательной к кривой σb - εb в точке с заданным напряжением:
Для расчета используют модуль упругопластичности бетона (тангенс угла наклона секущей в точке на кривой σb - εb с заданным напряжением):
Так как угол α1 меняется в зависимости от напряжений и времени, модуль упругопластичности также является переменной величиной, меньше, чем начальный модуль упругости.
Коэффициент νb меняется от 1 (при упругой работе) до 0,15.
С увеличением уровня напряжений в бетоне и длительности действия нагрузки, коэффициент νb уменьшается.
Модуль деформации бетона
116

Геометрическая интерпретация:
Модуль полных деформаций бетона при сжатии Eb соответствует полным деформациям (включая ползучесть) является переменной величиной; геометрически он определяется как тангенс угла наклона касательной к кривой σb - εb в точке с заданным напряжением:
Для расчета используют модуль упругопластичности бетона (тангенс угла наклона секущей в точке на кривой σb - εb с заданным напряжением):
Так как угол α1 меняется в зависимости от напряжений и времени, модуль упругопластичности также является переменной величиной, меньше, чем начальный модуль упругости.
Коэффициент νb меняется от 1 (при упругой работе) до 0,15.
С увеличением уровня напряжений в бетоне и длительности действия нагрузки, коэффициент νb уменьшается.
При изгибе железобетонных элементов для бетона сжатой зоны E/b может быть на 15…20% больше, чем при осевом сжатии.
Модуль деформации бетона
116

Геометрическая интерпретация:
Модуль полных деформаций бетона при сжатии Eb соответствует полным деформациям (включая ползучесть) является переменной величиной; геометрически он определяется как тангенс угла наклона касательной к кривой σb - εb в точке с заданным напряжением:
Для расчета используют модуль упругопластичности бетона (тангенс угла наклона секущей в точке на кривой σb - εb с заданным напряжением):
Так как угол α1 меняется в зависимости от напряжений и времени, модуль упругопластичности также является переменной величиной, меньше, чем начальный модуль упругости.
Коэффициент νb меняется от 1 (при упругой работе) до 0,15.
С увеличением уровня напряжений в бетоне и длительности действия нагрузки, коэффициент νb уменьшается.
При изгибе железобетонных элементов для бетона сжатой зоны E/b может быть на 15…20% больше, чем при осевом сжатии.
Модуль деформации бетона
116

Так как угол α1 меняется в зависимости от напряжений и времени, модуль упругопластичности также является переменной величиной, меньше, чем начальный модуль упругости.
Коэффициент νb меняется от 1 (при упругой работе) до 0,15.
С увеличением уровня напряжений в бетоне и длительности действия нагрузки, коэффициент νb уменьшается.
При изгибе железобетонных элементов для бетона сжатой зоны E/b может быть на 15…20% больше, чем при осевом сжатии.
Предельная растяжимость бетона в зависимости от временного сопротивления растяжению:
Модуль деформации бетона
116

Коэффициент νb меняется от 1 (при упругой работе) до 0,15.
С увеличением уровня напряжений в бетоне и длительности действия нагрузки, коэффициент νb уменьшается.
При изгибе железобетонных элементов для бетона сжатой зоны E/b может быть на 15…20% больше, чем при осевом сжатии.
Предельная растяжимость бетона в зависимости от временного сопротивления растяжению:
Начальный модуль упругости бетона при сжатии и растяжении может быть определен из специальных испытаний при низком уровне напряжений
Модуль деформации бетона
116

Предельная растяжимость бетона в зависимости от временного сопротивления растяжению:
Начальный модуль упругости бетона при сжатии и растяжении может быть определен из специальных испытаний при низком уровне напряжений
Существуют различные эмпирические формулы для определения Eb .
Для тяжелого бетона естественного твердения:
Модуль деформации бетона
116

Предельная растяжимость бетона в зависимости от временного сопротивления растяжению:
Начальный модуль упругости бетона при сжатии и растяжении может быть определен из специальных испытаний при низком уровне напряжений
Существуют различные эмпирические формулы для определения Eb .
Для тяжелого бетона естественного твердения:
Модуль сдвига:
Модуль деформации бетона
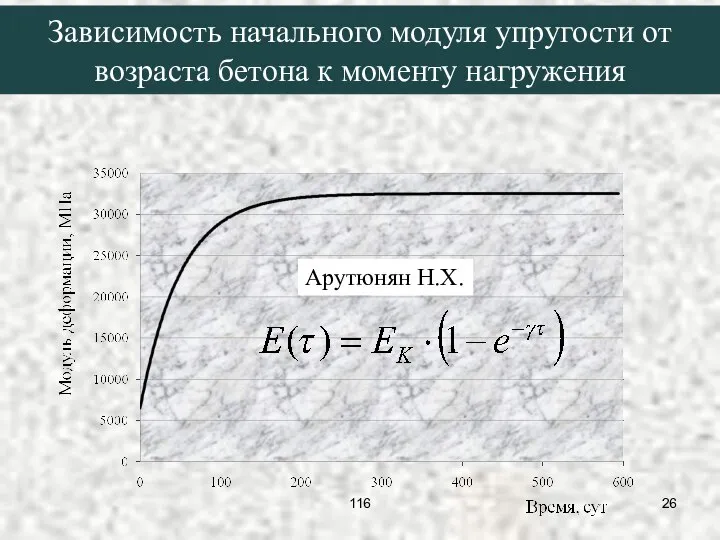
116

Зависимость начального модуля упругости от возраста бетона к моменту нагружения
Арутюнян Н.Х.
116

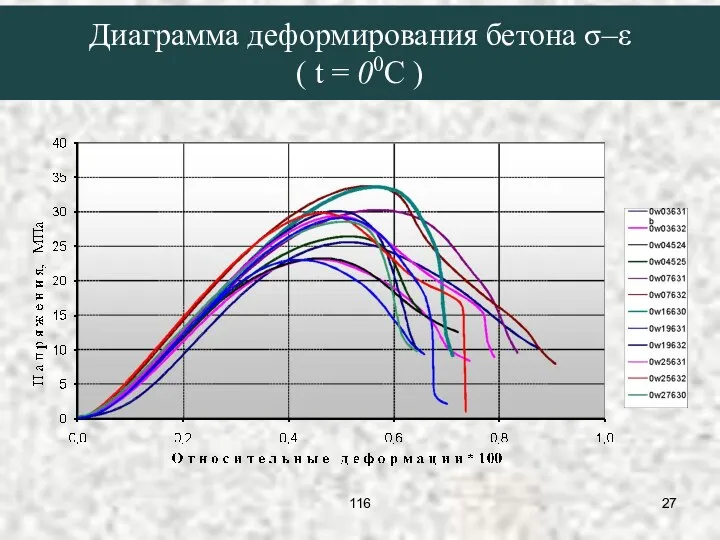
Диаграмма деформирования бетона σ–ε
( t = 00C )
116

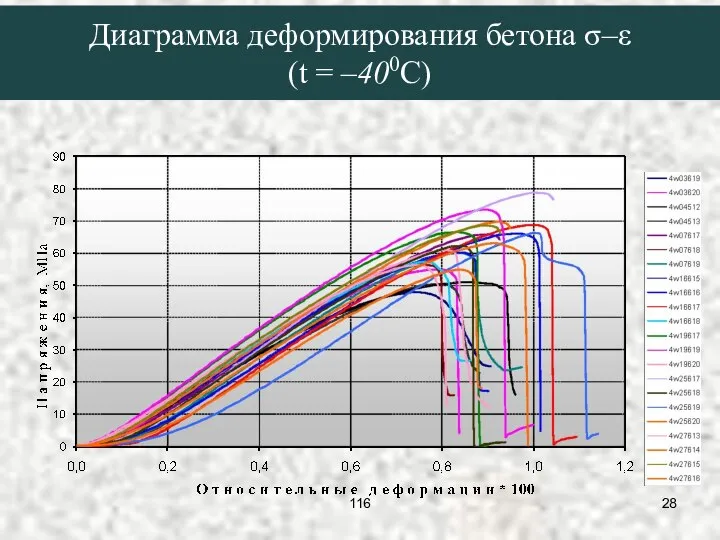
Диаграмма деформирования бетона σ–ε
(t = –400C)
116

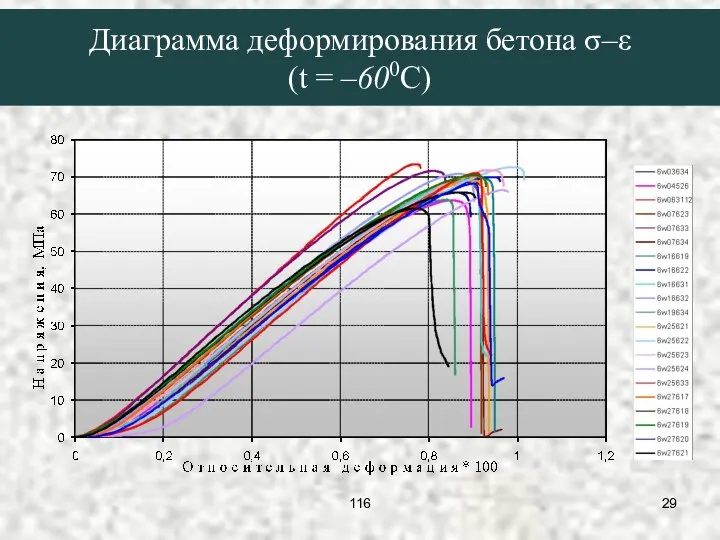
Диаграмма деформирования бетона σ–ε
(t = –600C)
116

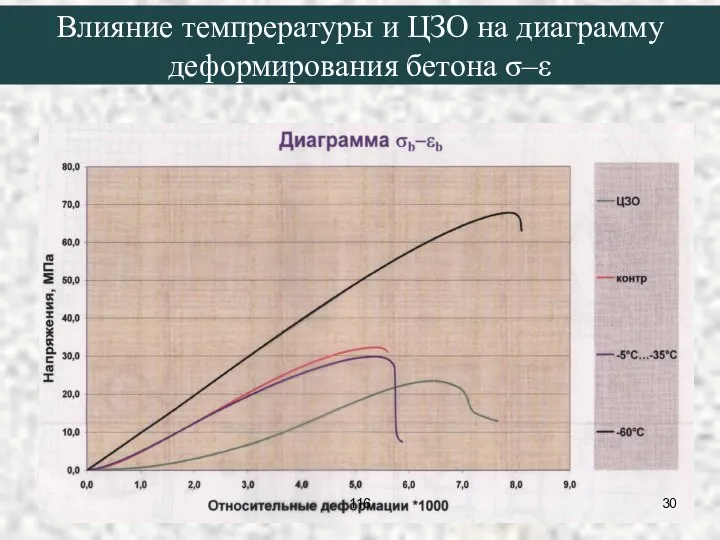
Влияние темпрературы и ЦЗО на диаграмму деформирования бетона σ–ε
116

Плотный силикатный бетон – бесцементный бетон автоклавного твердения, на основе известкового вяжущего (известково-песчаного, известково-шлакового).
Самостоятельно:
116

Плотный силикатный бетон – относятся к группе тяжелых бетонов с заполнителем из кварцевых песков.
Обладает хорошим сцеплением с арматурой и защищает ее от коррозии.
Eb в 1,5…2 раза меньше, чем у равнопрочного цементного бетона.
В неблагоприятных условиях (большие динамические нагрузки, усиленное воздействие атмосферных осадков) применение ограничено.
Самостоятельно:
116

Кислотостойкий бетон. Применяют пуццолановый портландцемент, шлаковый портландцемент, жидкое стекло применяется для конструкций подземных сооружений, покрытий некоторых цехов химической промышленности, цветной металлургии.
Самостоятельно:
116

Бетонополимеры. Бетон на цементном вяжущем с последующей пропиткой полимерными материалами по специально разработанной технологии. Имеют улучшенные физико-механические свойства. Используется при изготовлении напорных труб, дорожных плит, колонн, ригелей и др.
Самостоятельно:
116