Преобразование графиков. Тригонометрические функции. Алгебра и начала анализа. 10 класс

1. У = - f(x) ← y = f(x) , симметрия относительно оси ОХ.
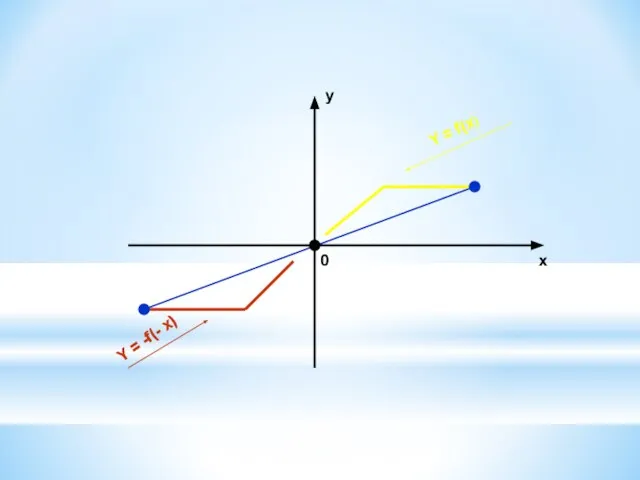
2. У = f(- x) ← y = f(x), симметрия относительно оси ОУ.
3. У = - f (- x) ← y = f(x), симметрия относительно начала координат.
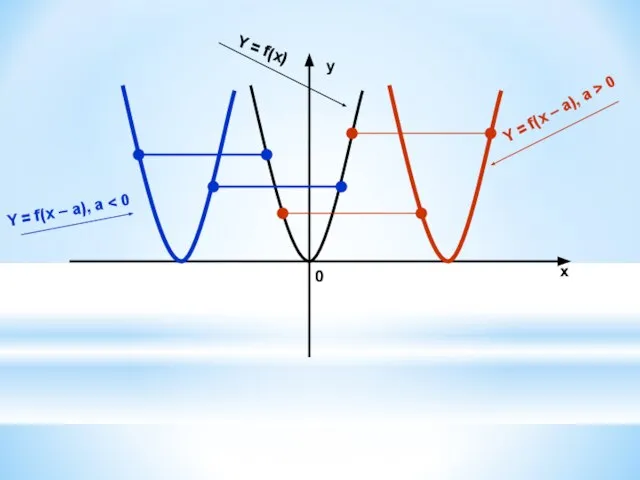
4. У = f(x – a) ← y = f(x),параллельным переносом вправо по ОХ, если а >0,
влево по ОХ, если а < 0.
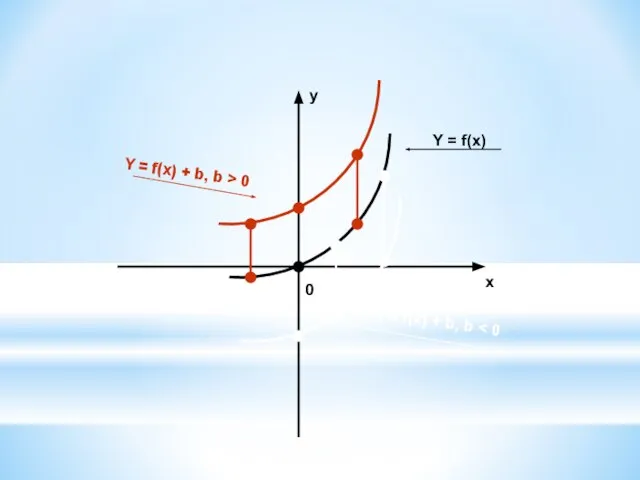
5. У = f(x) + b ← y = f(x), параллельным переносом вверх по ОУ, если в > 0,
вниз по ОУ, если в < 0.
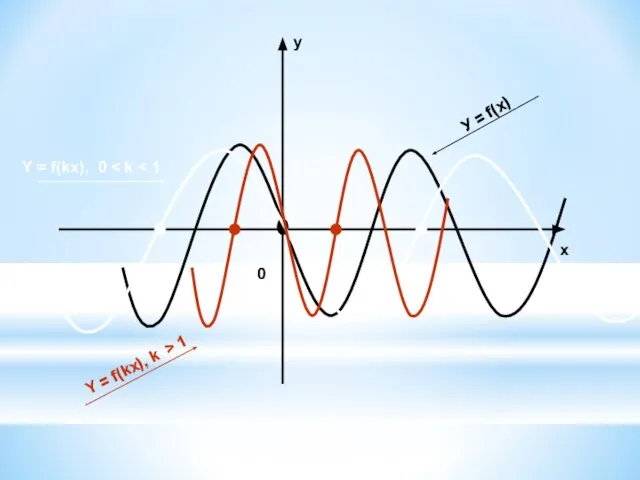
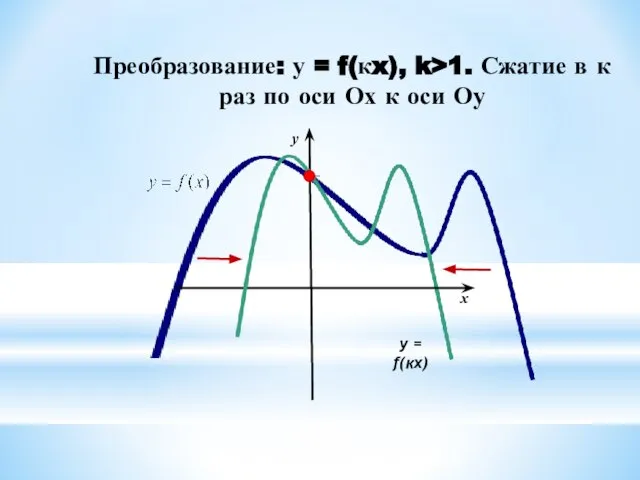
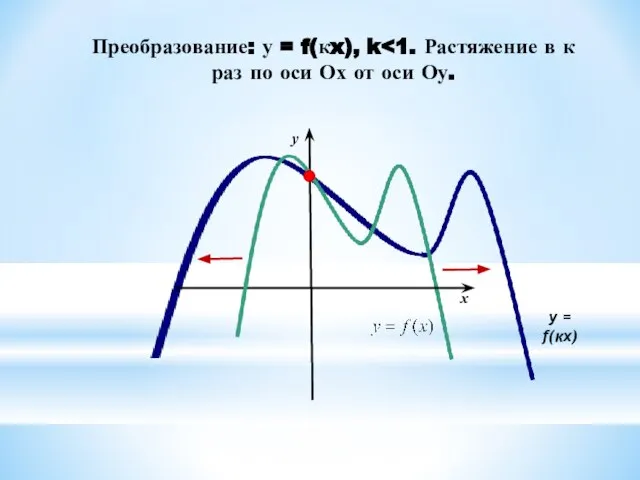
6. У = f(kx) ← y = f(x), растяжением в вдоль оси ОХ в 1/к раз, если 0 < к < 1;
сжатием вдоль оси ОХ в к раз, если к > 1.
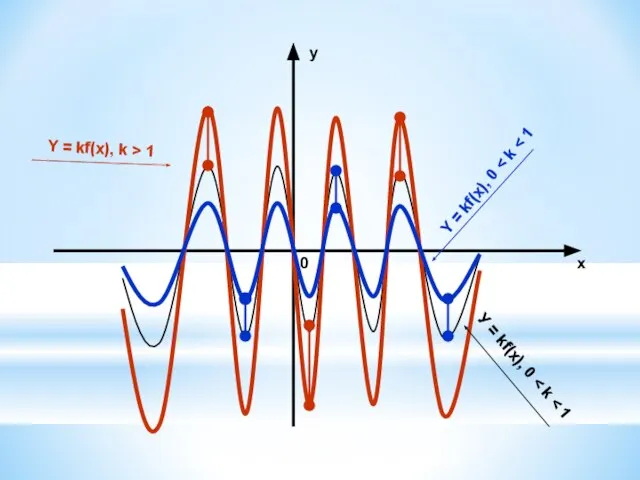
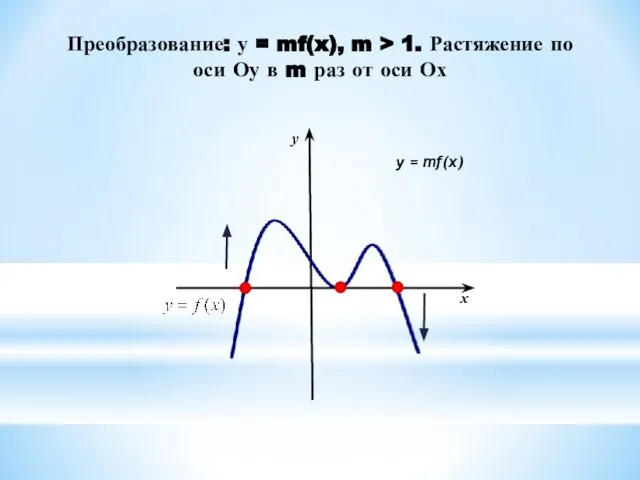
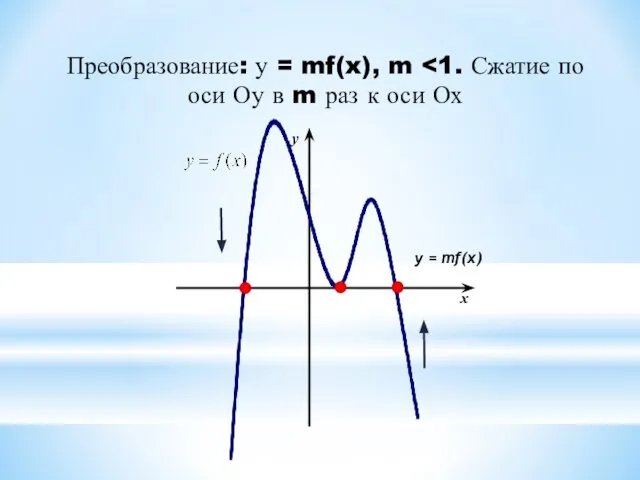
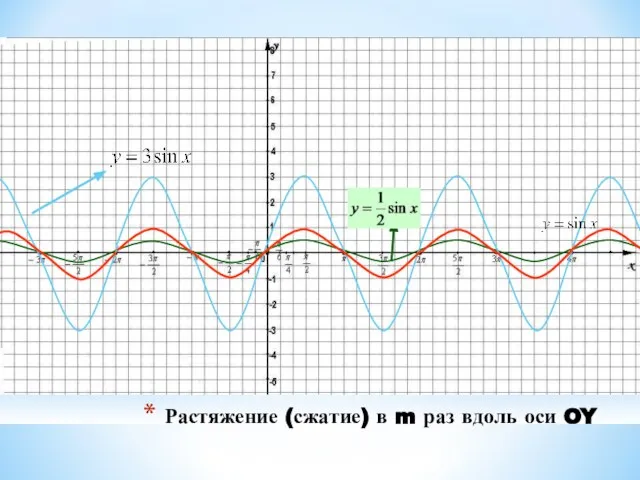
7. У = kf(x) ← y = f(x), сжатием вдоль оси ОУ в 1/к раз, если 0 < к < 1 и
растяжением вдоль оси ОУ в к раз, если к > 1.
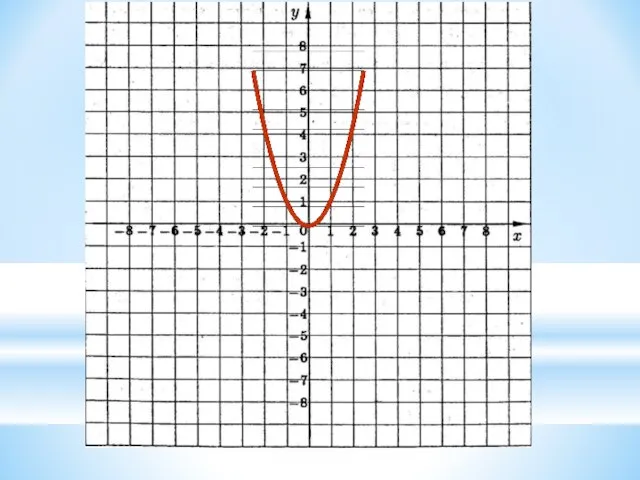
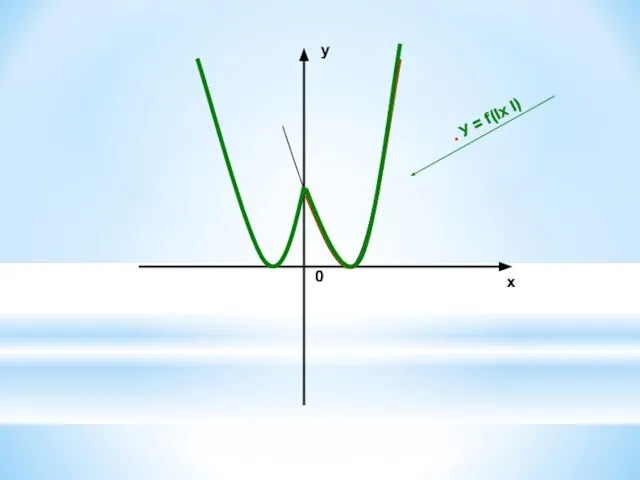
9. У = f(Ix I) ← y = f(x) строим график функции y = f(x) при х ≥ 0 и
отображаем его относительно оси ОУ.
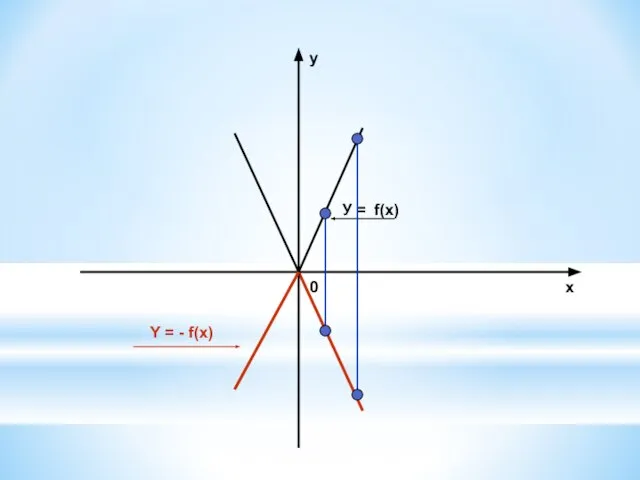
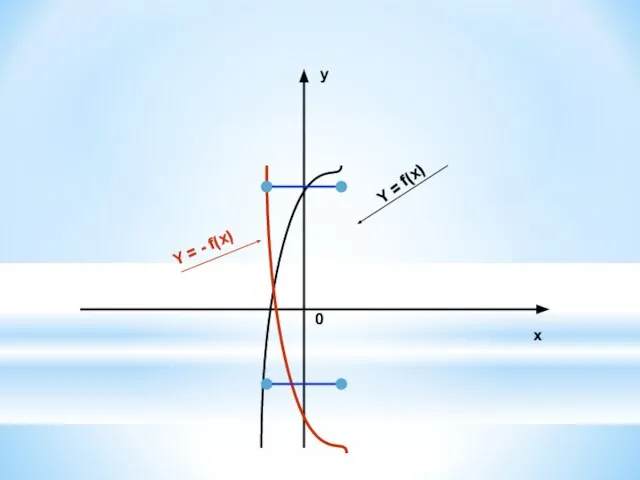
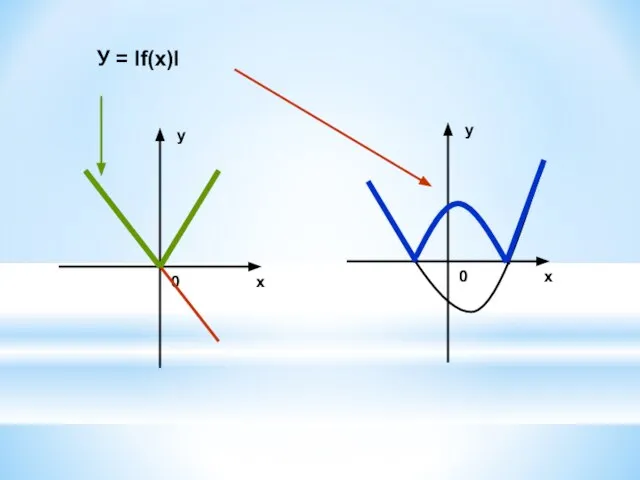
8. У = If(x)I – совпадает с у = f(x) в тех точках, которые лежат выше оси ОХ
симметричен графику у = f(x) относительно оси абсцисс в остальных точках.
Виды преобразований графиков- повторение и изучение новых знаний.

х
у
0
У = f(x)
Y = - f(x)

x
y
0
Y = f(x)
Y = - f(x)

x
y
0
Y = f(x)
Y = -f(- x)

x
y
0
Y = f(x)
Y = f(x – a), a < 0
Y = f(x – a), a > 0

х
у
0
Y = f(x)
Y = f(x) + b, b > 0
Y = f(x) + b, b < 0

у
х
У = f(x)
Y = f(kx), 0 < k < 1
Y = f(kx), k > 1
0

у
х
0
У = kf(x), 0 < k < 1
Y = kf(x), k > 1
Y = kf(x), 0 < k < 1

y
x
0
y
x
0
У = If(x)I

y
x
0
. У = f(Ix I)

Преобразование: у = mf(x), m > 1. Растяжение по оси Оу в m раз от оси Ох
x
y
у = mf(x)

x
y
у = mf(x)
Преобразование: у = mf(x), m <1. Сжатие по оси Оу в m раз к оси Ох

Растяжение (сжатие) в m раз вдоль оси OY

Преобразование: у = f(кx), k>1. Сжатие в к раз по оси Ох к оси Оу
x
y
у = f(кx)

Преобразование: у = f(кx), k<1. Растяжение в к раз по оси Ох от оси Оу.
x
y
у = f(кx)