Содержание
- 2. ДВИЖЕНИЯ Образуют специальный класс преобразований, играющих особую роль в различных науках и их приложениях и широко
- 3. ДВИЖЕНИЕ или ПЕРЕМЕЩЕНИЕ - это преобразование плоскости, сохраняющее расстояния
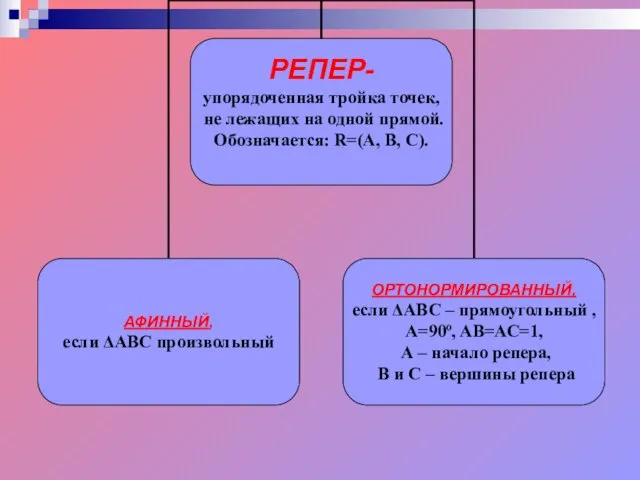
- 5. При движении репер R, образованный точками A, В, С, переходит в репер R', образованный точками A',
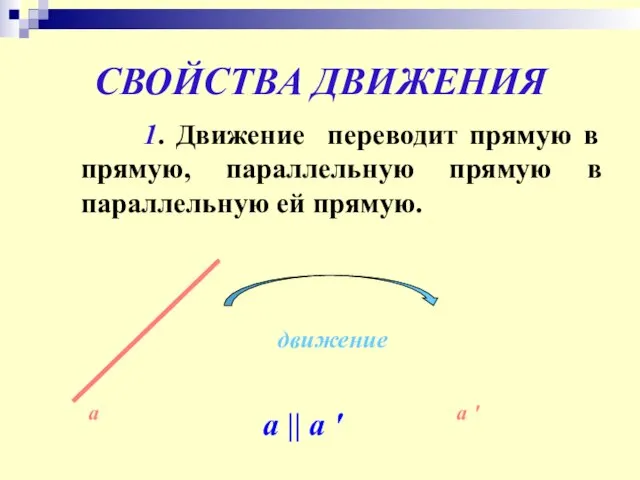
- 6. СВОЙСТВА ДВИЖЕНИЯ 1. Движение переводит прямую в прямую, параллельную прямую в параллельную ей прямую. а движение
- 7. СВОЙСТВА ДВИЖЕНИЯ 2. Движение переводит полуплоскость с границей A в полуплоскость c границей А', где А'
- 8. СВОЙСТВА ДВИЖЕНИЯ 3. Движение сохраняет простое отношение трех точек прямой. А В С λ =AC :
- 9. СВОЙСТВА ДВИЖЕНИЯ 4. Движение сохраняет отношение «лежать между». 5. Движение переводит отрезок AB в отрезок A'B'.
- 10. СВОЙСТВА ДВИЖЕНИЯ 6. Движение переводит угол в равный ему угол, луч в луч A A1 A=
- 11. СВОЙСТВА ДВИЖЕНИЯ 7. Движение переводит взаимно перпендикулярные прямые во взаимно перпендикулярные прямые а b a' b'
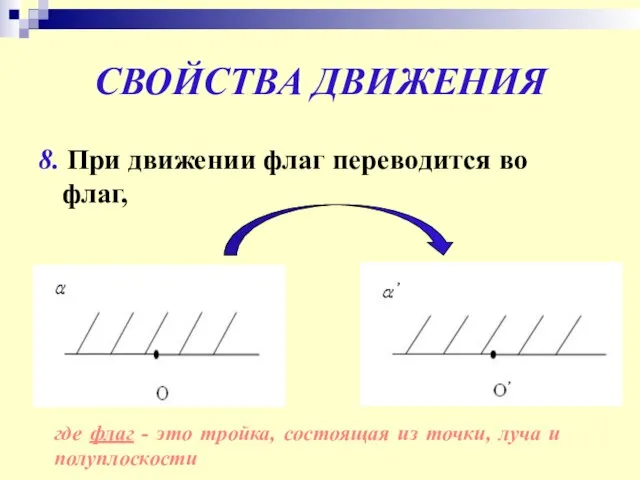
- 12. СВОЙСТВА ДВИЖЕНИЯ 8. При движении флаг переводится во флаг, где флаг - это тройка, состоящая из
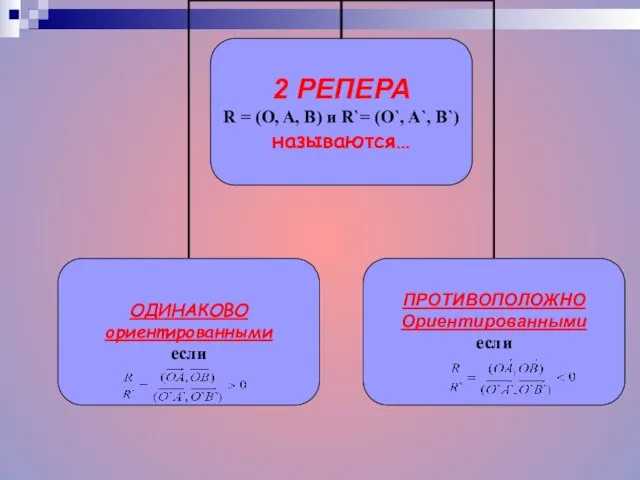
- 14. Преобразование точек плоскости сохраняет ориентацию плоскости или меняет ориентацию плоскости, если любой репер и его образ
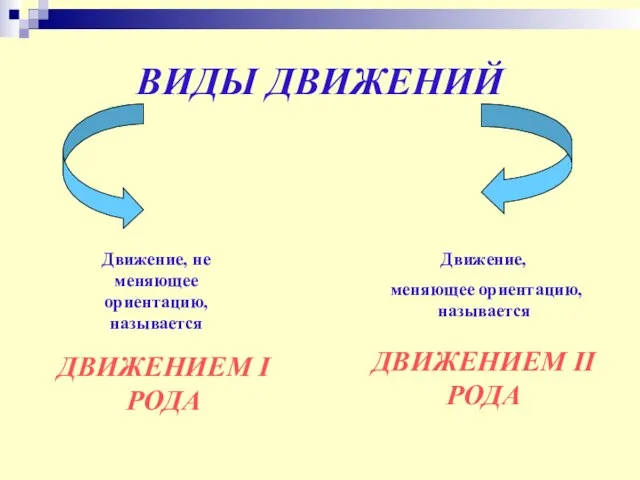
- 15. ВИДЫ ДВИЖЕНИЙ Движение, не меняющее ориентацию, называется ДВИЖЕНИЕМ I РОДА Движение, меняющее ориентацию, называется ДВИЖЕНИЕМ II
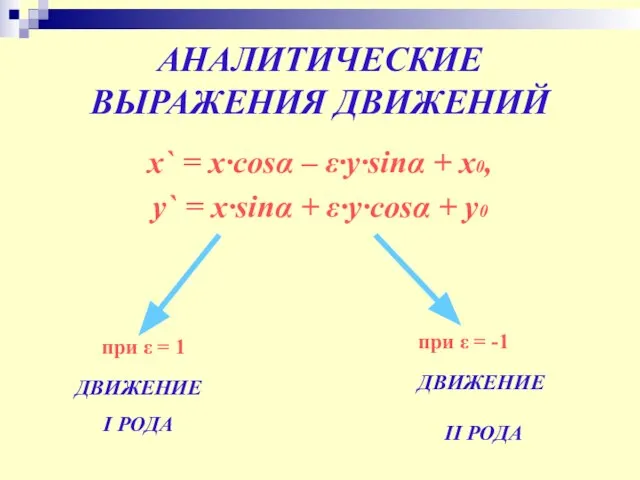
- 16. АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДВИЖЕНИЙ x` = x∙cosα – ε∙y∙sinα + x0, y` = x∙sinα + ε∙y∙cosα +
- 17. ДВИЖЕНИЕ I РОДА 1. Поворот на угол А М М1 Аналитические выражения: x` = x∙cosα –
- 18. ДВИЖЕНИЕ I РОДА 2. а)Параллельный перенос на Аналитические выражения: x` = x+х0 y` =y б) Параллельный
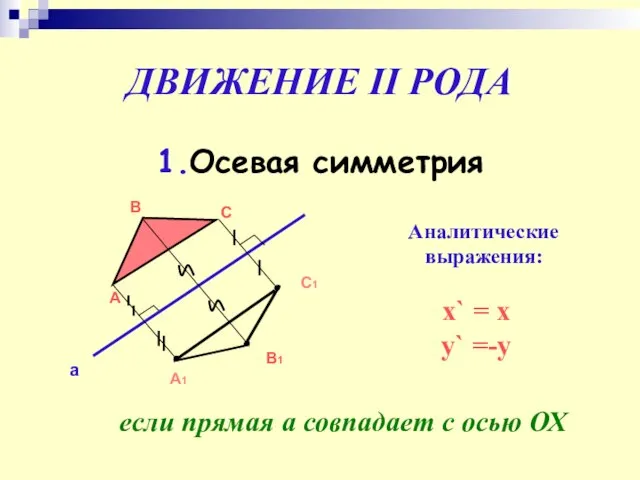
- 19. ДВИЖЕНИЕ II РОДА 1.Осевая симметрия А В С а С1 А1 В1 Аналитические выражения: x` =
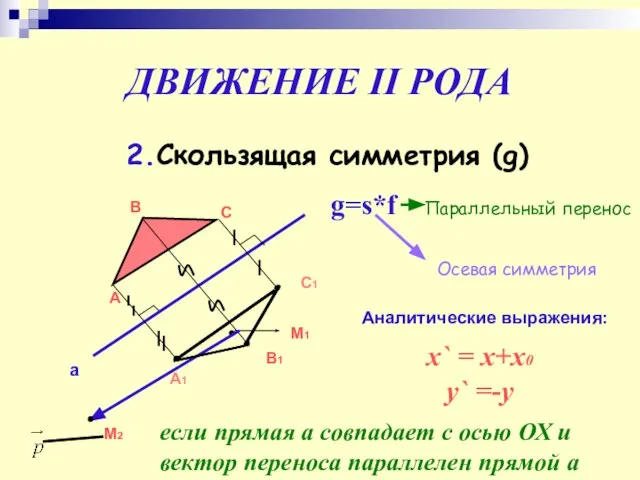
- 20. ДВИЖЕНИЕ II РОДА 2.Скользящая симметрия (g) А В С а С1 А1 В1 g=s*f Осевая симметрия
- 21. ПРЕОБРАЗОВАНИЕ ПОДОБИЯ Преобразование плоскости называется преобразованием подобия, если существует k > 0, такое что для любых
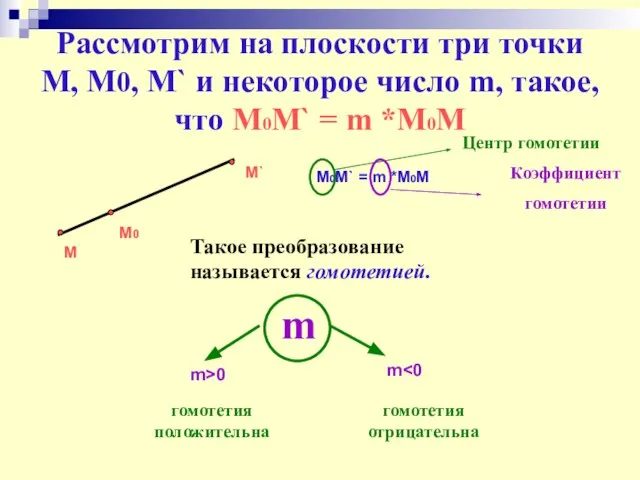
- 22. Рассмотрим на плоскости три точки М, М0, M` и некоторое число m, такое, что М0M` =
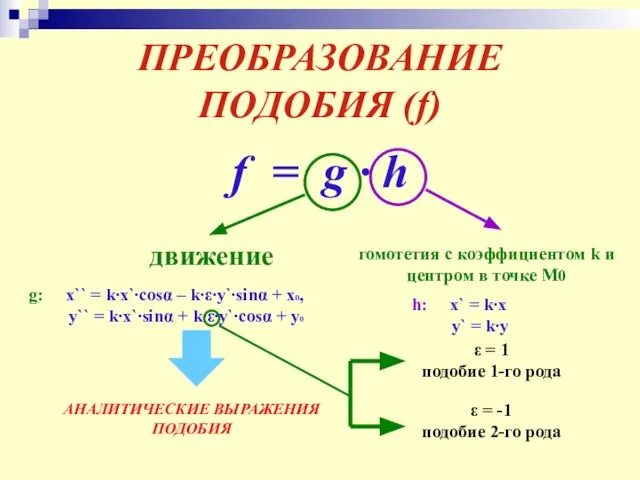
- 23. ПРЕОБРАЗОВАНИЕ ПОДОБИЯ (f) f = g ∙ h движение гомотетия с коэффициентом k и центром в
- 24. ПОДОБИЕ I РОДА Аналитические выражения: x` = k∙x∙cosα – k∙y∙sinα + x, y` = k∙y∙sinα +
- 25. 2. Параллельный перенос на О О1 Аналитические выражения: x` = k∙x+ x0, y` = k∙y+ y0
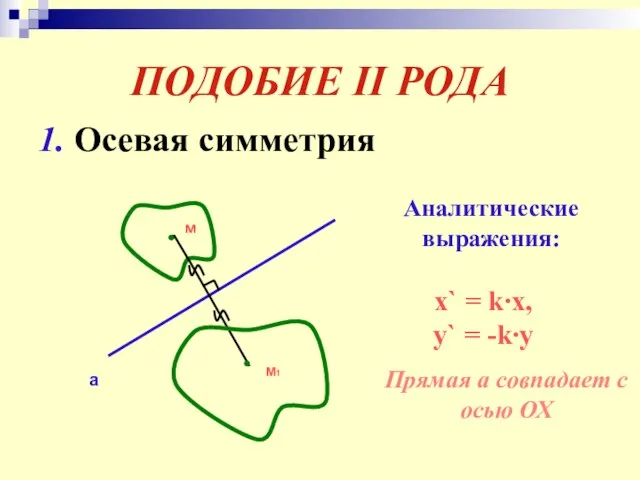
- 26. ПОДОБИЕ II РОДА 1. Осевая симметрия м а М1 Аналитические выражения: x` = k∙x, y` =
- 27. ПОДОБИЕ II РОДА 2. Скользящая симметрия x y М М1 М’ Аналитические выражения: x` = k∙x+x0,
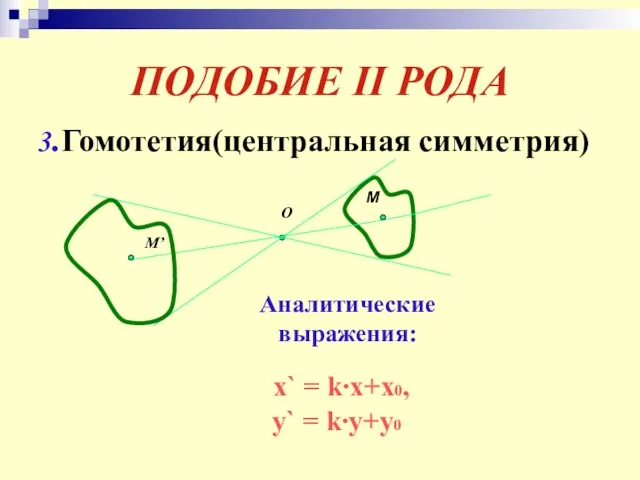
- 28. ПОДОБИЕ II РОДА 3.Гомотетия(центральная симметрия) О М М’ Аналитические выражения: x` = k∙x+x0, y` = k∙y+y0
- 30. Скачать презентацию















 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ»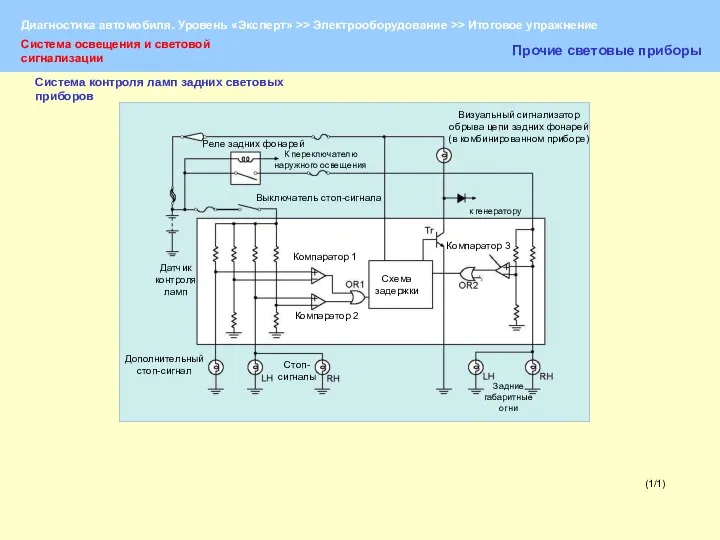 Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс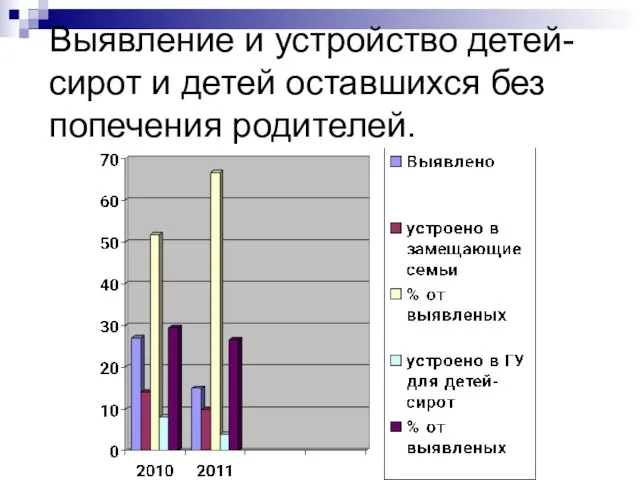 Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства