Содержание
- 2. Введение ПРОБЛЕМА: Учащиеся не всегда умеют сознательно использовать информацию об иррациональных уравнениях. Грамотно применять свойства корней
- 3. " Посредством уравнений, теорем Я уйму всяких разрешал проблем" (Чостер, английский поэт, средние века) "Уравнение -
- 4. Ход урока Организация урока. (1мин.) Постановка целей, принятие их учащимися.(2 мин.) Вопрос, раскрывающий сущность проблемы. Дискуссия
- 5. Начало урока Здравствуйте! Надеюсь ,что у вас серьезный настрой на урок. Желаю вам высоких результатов. В
- 6. 2.Вопрос - проблема Какой шаг в решении уравнения приводит к появлению лишних корней.
- 7. Найди ошибку. 16 -36 =25 – 45 16-36+20,25=25-45+20,25 (4-4,5)² =(5-4,5)² 4-4,5=5-4,5 4=5 Вывод: Если квадраты двух
- 8. 3. Изучение нового материала. Уравнения, в которых переменная содержится под знаком корня, называются иррациональными. Устно: какие
- 9. 4. Первичное осмысление. √ х – 6 = 2 √ х – 3 = 0 √
- 10. Алгоритм решения уравнений. Решение иррациональных уравнений сводится к переходу от иррационального к рациональному уравнению путем возведения
- 11. 5. Закрепление изученного материала. Является ли число x корнем уравнения: а) √ х – 2 =
- 12. Решим уравнение: √ х + 2 = х Решение: х + 2 = х2, х2 –
- 13. Решим уравнение. √2х – 3 = √ х - 2
- 14. Решение Возведем обе части уравнения в квадрат, получим: 2х -3 = х -2 , х =
- 15. История неразумных чисел История иррациональных чисел относится к удивительному открытию пифагорийцев. А началось это с простого
- 16. 6. Задание на дом. № 900 ( г, д, е ) № 901 ( а, г
- 18. Скачать презентацию











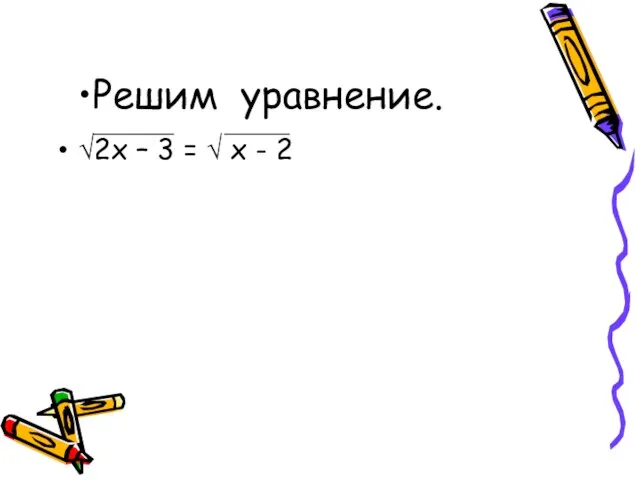



 Интернет ресурсы по правам потребителя
Интернет ресурсы по правам потребителя Рукокрылые
Рукокрылые Health is the Greatest wealth
Health is the Greatest wealth Красноярские художники XXI века
Красноярские художники XXI века Как мы влюбляемся? И почему?
Как мы влюбляемся? И почему? Великобритания
Великобритания Кредитный потребительский кооператив «ПЕРВЫЙ ДАЛЬНЕВОСТОЧНЫЙ»
Кредитный потребительский кооператив «ПЕРВЫЙ ДАЛЬНЕВОСТОЧНЫЙ» Загрязнение вод
Загрязнение вод ОСНОВЫ РЕЛИГИОЗНЫХ КУЛЬТУР И СВЕТСКОЙ ЭТИКИ
ОСНОВЫ РЕЛИГИОЗНЫХ КУЛЬТУР И СВЕТСКОЙ ЭТИКИ Краткий словарь современных профессий
Краткий словарь современных профессий Sibnet.ru сибирский информационно-развлекательный портал. более 4 000 000 уникальных пользователей в месяц* более 2 500 000 просмотров ежесут
Sibnet.ru сибирский информационно-развлекательный портал. более 4 000 000 уникальных пользователей в месяц* более 2 500 000 просмотров ежесут Деревня Юрьевец
Деревня Юрьевец Breyn-ring. Предприниматели и предпринимательство
Breyn-ring. Предприниматели и предпринимательство ОДИН ДОМА. ПРАВИЛА ПОВЕДЕНИЯ
ОДИН ДОМА. ПРАВИЛА ПОВЕДЕНИЯ Круговорот воды в природе
Круговорот воды в природе K.Borutos romano „Baltaragio malūnas” veikėjai (2 pam.) Pirmoje pamokoje buvo aptartas velnio Pinčuko paveikslas
K.Borutos romano „Baltaragio malūnas” veikėjai (2 pam.) Pirmoje pamokoje buvo aptartas velnio Pinčuko paveikslas ПРЕЗЕНТАЦИЯ Подписка Sixt Газ
ПРЕЗЕНТАЦИЯ Подписка Sixt Газ Урок русского языка в 5 классе
Урок русского языка в 5 классе 16 и 19 ноября 124
16 и 19 ноября 124 1 ИЮНЯ ДЕНЬ ЗАЩИТЫ ДЕТЕЙ.
1 ИЮНЯ ДЕНЬ ЗАЩИТЫ ДЕТЕЙ. «…Металлургическая отрасль должна стать в первых рядах форсированного индустриально-инновационного развития…» Н.А. Назарбаев
«…Металлургическая отрасль должна стать в первых рядах форсированного индустриально-инновационного развития…» Н.А. Назарбаев Ноктурия и ее влияние на качество жизни
Ноктурия и ее влияние на качество жизни Спорт как социальное явление
Спорт как социальное явление Урок лыжной подготовки в 9 классе
Урок лыжной подготовки в 9 классе Стратегический План на 2008-2011 годыДля обсуждения с НПО22 февраля 2008 г.
Стратегический План на 2008-2011 годыДля обсуждения с НПО22 февраля 2008 г. Конфликты супругов пожилого возраста
Конфликты супругов пожилого возраста Методы и методики исследования влияния видеоигр на деятельность психики
Методы и методики исследования влияния видеоигр на деятельность психики Способы создания образов воображения
Способы создания образов воображения