Презентация на тему Построение правильных многоугольников циркулем и линейкой

Цель урока
Создать условия для более глубокого усвоения знаний по теме, высокого уровня обобщения и систематизации знаний.

Методические задачи
Выяснить , всякий ли правильный многоугольник можно построить с помощью циркуля и линейки;
Повторить способы построения правильных многоугольников и познакомить с новыми способами;
Познакомить с приближенными построениями правильных многоугольников (способы А Дюрера, Биона, Ф.Коваржика);
Познакомить с перспективными технологиями и новыми разработками построения правильных многоугольников;
Показать применение правильных многоугольников в окружающем нас мире.

Выпуклые и невыпуклые многоугольники
Многоугольник- это фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
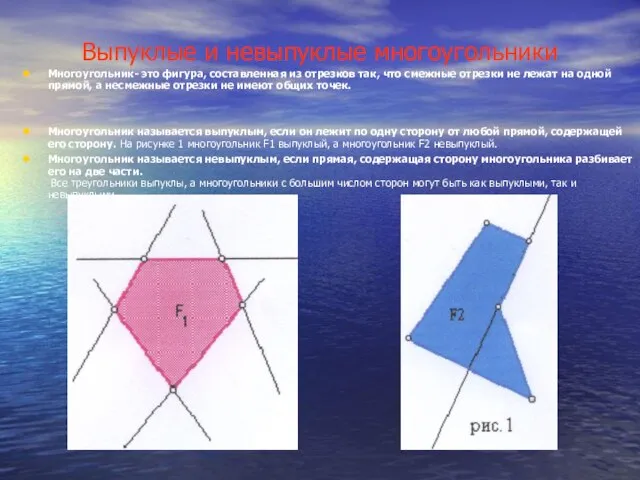
Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону. На рисунке 1 многоугольник F1 выпуклый, а многоугольник F2 невыпуклый.
Многоугольник называется невыпуклым, если прямая, содержащая сторону многоугольника разбивает его на две части. Все треугольники выпуклы, а многоугольники с большим числом сторон могут быть как выпуклыми, так и невыпуклыми.

Правильные многоугольники
На рисунке 1 представлены правильный треугольник , шестиугольник и четырех угольник.

Около любого правильного многоугольника можно описать окружность, и притом только одну, и также в любой правильный многоугольник можно вписать окружность, и притом только одну. Центры описанной около правильного многоугольника и вписанной в него окружностей совпадают. Радиус описанного круга -это радиус правильного многоугольника, а радиус вписанного круга –его апофема.
Правильные многоугольники всегда выпуклые, но существуют и самопересекающиеся замкнутые ломаные, имеющие равные звенья и углы. Фигуры такого вида называются правильными звездчатыми многоугольниками или полиграммами, по аналогии с пентаграммой - правильной пятиконечной звездой (изображена внутри правильного пятиугольника на рис.2).
Любой правильный многоугольник, выпуклый или звездчатый, можно наложить сам на себя так, чтобы одна из двух произвольно заданных сторон совпала с другой; то же верно для любых двух его вершин. И обратно: многоугольник, обладающий обоими этими свойствами, правильный. Но существуют неправильные многоугольники, у которых такое свойство справедливо только для сторон, как у ромба, или только для вершин, как у прямоугольника.
Имеется 2n способов совместить правильный n-угольник сам с собой: половина из них - повороты вокруг одной и той же точки, его центра, на углы, кратные360°/ n, вторая половина - n симметрий относительно прямых, соединяющих центр с вершинами и серединами сторон. Центр правильного многоугольника равноудален от всех его сторон и от всех вершин, поэтому он служит одновременно центром вписанной и описанной окружностей многоугольника (рис.3 )

Великий математик, механик и инженер древности Архимед
(греч.(греч. Αρχιμήδης, родился 287 до н. э.(греч. Αρχιμήδης, родился 287 до н. э. - 212 до н. э.)
Периметр (сумма длин сторон) правильного n-угольника при заданном числе сторон n наиболее близок к длине его описанной окружности среди всех вписанных в нее n-угольников; таким же свойством он обладает и по отношению к вписанной окружности. Поскольку вычисление длины окружности считалось в древности весьма важной задачей, много усилий было затрачено на то, чтобы научиться оценивать периметр вписанной в нее правильного многоугольника при достаточно больших n. Особенно преуспел в этом Архимед.

Евклид
( родился в 330 году до н. э. в небольшом городке Тире, недалеко от Афин).
Впрочем, правильные многоугольники привлекали внимание древнегреческих учёных задолго до Архимеда. Пифагорейцы, в философии которых числа играли главную роль, придавали очень большое значение задаче о делении окружности на равные части, т. е. о построении правильного вписанного многоугольника. В "Началах" Евклида приводятся построения с помощью циркуля и линейки правильных многоугольников с числом сторон от трёх до шести, а также пятнадцати угольника. Этим последним особенно интересовались: согласно измерениям древних астрономов, угол наклона плоскости эклиптики к экватору равнялся 1/5 полного угла, т.е. 24°(истинное значение чуть меньше -23°27'). Задача о построение правильных многоугольников была полностью решена лишь спустя два тысячелетия.

Теорема. Многоугольник, вписанный в окружность, является выпуклым. Если все стороны вписанного многоугольника равны, то он является правильным.
Доказательство. Рассмотрим многоугольник А1А2…Аn, вписанный в окружность с центром О. Докажем сначала, что этот многоугольник выпуклый. Для этого нужно доказать, что он лежит по одну сторону от любой прямой, содержащей сторону многоугольника. Докажем, например, что он лежит по одну сторону от прямой А1А2. Для этого достаточно убедиться в том, что вершины А3А4,…, Аn принадлежат одной и той же полуплоскости с границей А1А2. Рассмотрим полуплоскость с границей А1А2, в которой лежит точка А3. Точка А4 принадлежит этой же полуплоскости, так как в противном случае прямая А1А2 пересекает дугу А3А4 окружности и, следовательно, имеет с окружностью больше двух точек, что невозможно. Точно так же вершина А5 и все остальные вершины принадлежат этой же полуплоскости. Аналогично доказывается, что многоугольник лежит по одну сторону от каждой из этих прямых А2А3 ,…, АnА1.
Пусть все стороны вписанного многоугольника равны: А1А2 = А3А4 =…= Аn-1Аn = АnА1. Докажем, что углы многоугольника также равны: угол А1= угол А2=…=угол Аn. Если n=3, то это утверждение очевидно. Допустим, что n >3, и рассмотрим вершины Аn, А1, А2, А3 (рис.4).
Треугольники ОАnА1, ОА1А2, ОА2А3 равны друг другу по трем сторонам, а так как эти треугольники равнобедренные, то угол1= угол 2=угол 3= угол 4. Поэтому угол А1= угол1+угол 2= угол 3+ угол 4= угол А2. Точно также доказывается равенство других углов многоугольника. Следовательно, многоугольник А1А2…Аn правильный.

Каково бы ни было число n, больше двух, существует правильный n-угольник.
Возьмем какую-нибудь окружность с центром в точке О и разделим её на n равных дуг. Для этого проведем радиусы ОА1, ОА2,…, ОАn этой окружности так, чтобы угол А1ОА2= угол А2ОА3 =…= угол Аn-1ОАn= угол АnОА1= 360°/n (рис.5, на этом рисунке n=8).
Если теперь провести отрезки А1А2, А2А3,…, Аn-1Аn, АnА1, то получим n- угольник А1А2…Аn. Треугольники А1ОА2, А2ОА3,…, АnОА1 равны друг другу (по двум сторонам и углу между ними), поэтому А1А2= А2А3=…= Аn-1Аn= АnА1. Отсюда согласно доказанной теореме следует, что А1А2…Аn- правильный n- угольник.
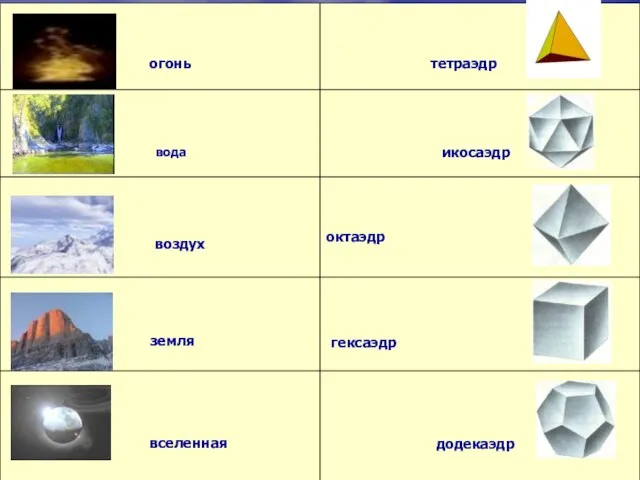
В пространстве фигурой, аналогичной правильному многоугольнику, является правильный многогранник- выпуклый многогранник, у которого все грани- правильные равные друг другу многоугольники и к каждой вершине которого сходится одно и то же число ребер. Примером правильного многогранника является куб. Интересно отметить, что в отличие от правильных многоугольников, которые могут иметь любое (больше двух) число сторон, существует лишь конечное число различных типов правильных многогранников. Ещё Евклид доказал, что таких типов только пять: четырехгранник (тетраэдр), шестигранник (куб), восьмигранник (октаэдр), двенадцатигранник (додекаэдр), двадцатигранник (икосаэдр).

Основные формулы.
Вычисление угла правильного многоугольника :
Сторона правильного многоугольника :
Площадь правильного
многоугольника :
Радиус вписанной окружности :

.Применение формул
Для правильного треугольника
Для правильного четырехугольника
Для правильного шестиугольника
Теорема. Правильные одноимённые многоугольники подобны и стороны их относятся как радиусы или апофемы.
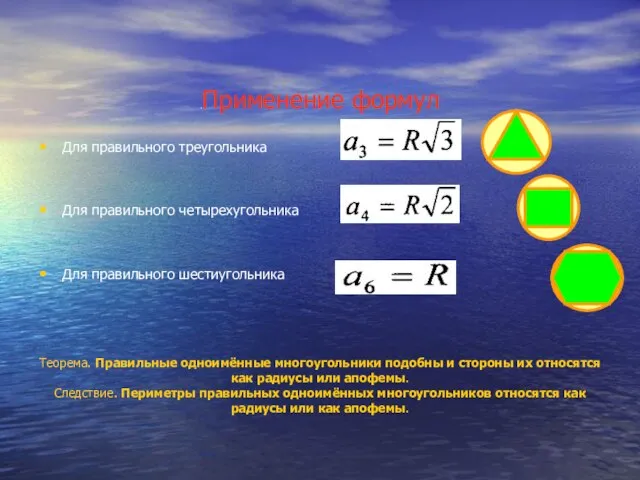
Следствие. Периметры правильных одноимённых многоугольников относятся как радиусы или как апофемы.

Построение правильного многоугольника
по его стороне (с использованием поворота)
Правильным называют многоугольник, у которого все стороны равны и все углы равны. Предварительно необходимо вычислить внутренний угол правильного многоугольника. Из школьного курса геометрии вам известно (или будет известно немного позже), что сумма углов выпуклого n-угольника равна 180o(n - 2). Исходя из этой теоремы, несложно вычислить величину внутреннего угла правильного многоугольника. В таблице ниже приведены значения сумм углов и внутренних углов для некоторых правильных многоугольников.
Зная величину внутреннего угла правильного многоугольника, построить сам многоугольник не составит труда.
Построим две точки - две соседние вершины многоугольника.
Одну из точек отметим как центр поворота, выделим вторую точку и повернём её на внутренний угол. В результате будет построена третья вершина многоугольника.
Только что построенную точку отметим в качестве центра поворота и повернём на внутренний угол соседнюю вершину (бывший центр). Будет построена четвёртая вершина.
Третий шаг будем повторять до тех пор, пока не будут построены все вершины многоугольника.
Последовательно соединить вершины многоугольника отрезками.

Любой ли правильный многоугольник можно построить
с помощью циркуля и линейки ?
Если построен какой-нибудь правильный n-угольник, то с помощью циркуля и линейки можно построить правильный 2n-угольник.
Опишем около данного многоугольника А1, А2… Аn oкружность. Для этого построим серединные перпендикуляры a и b к oтрезкам А1 А2 и А2 А3 ( на рисунке n= 4). Они пересекаются в некоторой точке О. Окружность с центром О радиуса ОА1 является описанной около многоугольника А1 А2…Аn. Построим теперь середины B1, B2, …, Bn соответственно дуг А1 А2, А2А3,…, Аn А1 следующим образом. Точки B1и B2 получаются как точки пересечения прямых а и b с дугами А1 А2 и А2 А3. Для построения точки B3 проведём oкружность с центром А3 радиуса А3 B2. Одна из точек пересечения этой oкружности с описанной окружностью есть точка B2, а другая - искомая точка B3. Аналогично строятся точки B4,…, Bn. Соединив каждую из точек B1,B2,…, Bn отрезками с концами соответствующей дуги, получим 2n-угольник А1В1А2В2А3… Аn Bn, который является правильным в силу теоремы о вписанном в окружность многоугольнике
На рисунке по данному правильному четырёхугольнику А1А2А3А4 построен правильный восьмиугольник А1В1А2…В4. Итак, если мы можем построить циркулем и линейкой правильный n-угольник, где n - данное натуральное число, то можно построить правильные 2n-угольник, 4n-угольник и, вообще, (2^k*n)-угольник, где k - любое натуральное число.

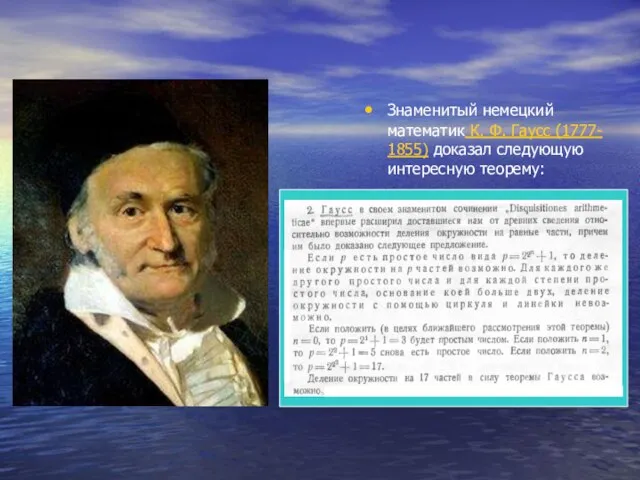
Знаменитый немецкий математик К. Ф. Гаусс (1777- 1855) доказал следующую интересную теорему:

Построение правильных многоугольников с помощью циркуля и линейки .
Задача №1. Построение правильного шестиугольника и треугольника.
Согласно формуле аn= 2R*sin180°/n сторона АВ правильного шестиугольника равна радиусу R описанной окружности. Поэтому, если задан произвольный отрезок PQ, то для построения правильного шестиугольника, стороны которого равны PQ, достаточно построить окружность радиуса PQ, взять на ней произвольную точку А и, не меняя раствора циркуля, отметить на этой окружности последовательно точки B, C, D, E, F так, чтобы AB=BC=…=EF=PQ. Проведя затем отрезки AB, BC, CD, DE, EF, FA, получим шестиугольник ABCDEF, который согласно теореме о правильном многоугольнике является правильным, причем его стороны равны отрезку PQ.
Для того, чтобы построить правильный треугольник нужно соединить точки данного шестиугольника через одну, значит соединим точки A,C и E. Треугольник ACE- искомый.

Задача №2. Построение правильного четырехугольника и восьмиугольника.
Пусть w-данная окружность с центром в точки О и радиусом R. Через точку О проведем диаметр АС и к этому диаметру проведем серединный перпендикуляр, который пересечет окружность w в двух точках В и D.Теперь последовательно соединим точки A,B,C и D. ABCD-искомый квадрат.
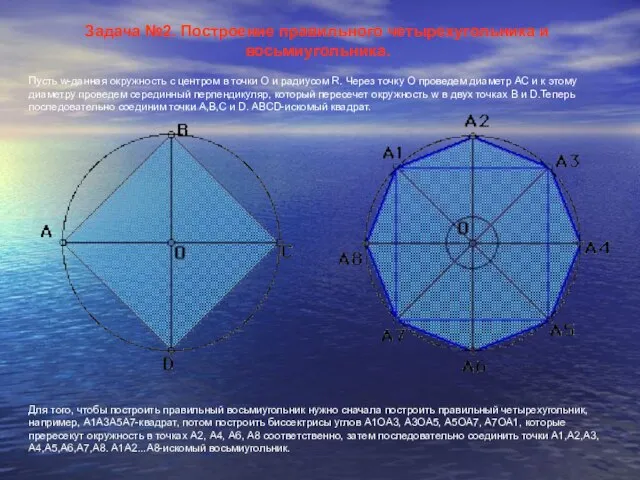
Для того, чтобы построить правильный восьмиугольник нужно сначала построить правильный четырехугольник, например, А1А3А5А7-квадрат, потом построить биссектрисы углов А1OА3, А3OА5, А5OА7, А7OА1, которые прересекут окружность в точках А2, А4, А6, А8 соответственно, затем последовательно соединить точки А1,А2,А3,А4,А5,А6,А7,А8. А1А2...А8-искомый восьмиугольник.

.
Задача №3. Найти углы правильного десятиугольника и выразить его сторону через радиус R описанной окружности.
Решение. По формуле аn=(n-2)/n*180° находим угол а10 правильного десятиугольника: а10=(10-2)/10*180°= 144°.
Пусть АВ- сторона правильного десятиугольника, вписанного в окружность радиуса R с центром в точке О.
По формуле аn= 2R*sin180°/n АВ=2R*sin18°. Получим другое выражение для стороны АВ. С этой целью рассмотрим треугольник АВО и проведем его биссектрису АС. Так как угол АОВ= 360°/10= 36°, то угол ОАВ= (180°-36°)/2= 72°, угол ВАС= 1/2*угол ОАВ= 1/2*72°= 36°.
Отсюда следует, что треугольник АОВ~ треугольнику САВ по двум углам (угол АОВ = угол ВАС= 36°, угол В -общий). Поэтому АВ=АС и АВ/ОВ= ВС/АВ. Далее, треугольник АОС равнобедренный (угол АОС= угол ОАС= 36°), следовательно, АС=ОС.
Итак, АВ=АС=ОС=R-BC, откуда ВС=R-АВ, и пропорцию АВ/ОВ=ВС/АВ можно записать в виде АВ/R=(R-AB)/AB. Отсюда получаем квадратное уравнение относительно АВ:
АВ + R*АВ -R =0. Решая это уравнение и учитывая, что АВ>0, находим АВ= R/2( 5-1) (Замечание. Сравнивая полученное выражение для АВ с равенством АВ=2R*sin18°, находим значение sin18°: sin18°= ( 5-1)/4

Задача 4. Построение правильного десятиугольника и пятиугольника.
Пусть w- данная окружность радиуса R c центром О. Построим сначала правильный десятиугольник, вписанный в окружность w. Для этого проведем взаимно перпендикулярные радиусы ОА1 и ОВ окружности w и на отрезке ОВ как на диаметре построим окружность с центром С. Отрезок А1С пересекает эту окружность в некоторой точке D. Докажем, что отрезок А1D равен стороне правильного десятиугольника, вписанного в окружность w. В самом деле,
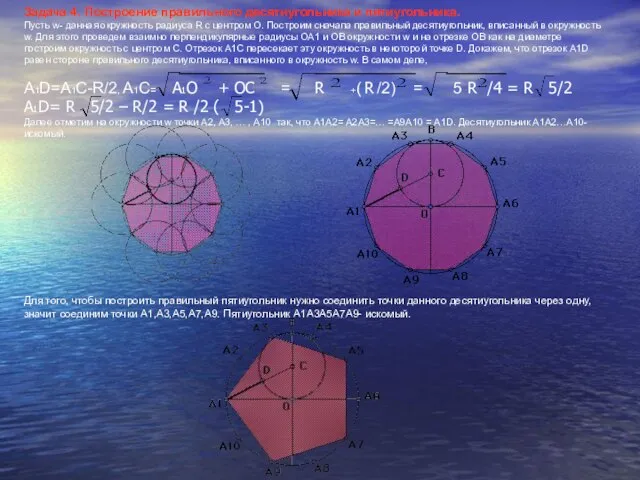
А1D=А1С-R/2, А1С= А1О + ОС = R +( R /2) = 5 R /4 = R 5/2
А1D= R 5/2 – R/2 = R /2 ( 5-1)
Далее отметим на окружности w точки А2, А3, … , А10 так, что А1А2= А2А3=… =А9А10 = А1D. Десятиугольник А1А2…А10-искомый.
Для того, чтобы построить правильный пятиугольник нужно соединить точки данного десятиугольника через одну, значит соединим точки А1,А3,А5,А7,А9. Пятиугольник А1А3А5А7А9- искомый.

.
Задача 5. В данную окружность вписать правильный пятнадцатиугольник.
Решение. Пусть w- данная окружность радиуса R с центром O и АВ - сторона правильного вписанного в эту окружность десятиугольника, а АС- сторона правильного вписанного шестиугольника, причем точки В и С расположены на окружности так, как показано на рисунке а). Тогда, очевидно, дуга АВ=36°, дуга АС=60° , поэтому дуга ВС=24° . Следовательно, угол ВОС=24°=360°/15°, и, значит, отрезок ВС- сторона правильного пятнадцатиугольника, вписанного в окружность w. Так как мы умеем строить циркулем и линейкой отрезки АВ=((корень из 5-1)/2)*R и АС=R (рис.б)), то можем построить отрезок ВС.
Возьмем далее на окружности w произвольную точку А1 и, пользуясь циркулем, отметим на этой окружности последовательно точки А2, А3,…, А15 так, что А1А2 = А2А3=…= А14А15= ВС. Проведя затем отрезки А1А2, А2А3,…, А14А15, А15А1, получим искомый правильный пятнадцатиугольник А1А2…А15 (рис. в)).

Задача №6. Дан правильный n-угольник А1А2...Аn, вписанный в окружность с центром О. Построить n-угольник, сторона которого равна данному отрезку PQ.
Решение. Проведем лучи ОА1, ОА2,..., ОАn и на этих лучах построим вершины искомого n-угольника. Для этого на луче А2А1 отложим отрезок А2С, равный отрезку PQ, и через точку С проведем прямую, параллельную прямой ОА2 (на рисунке n=8). Точку пересечения этой прямой с лучом ОА1 обозначим В1. Проведем теперь окружность с центром О радиуса ОВ1 и обозначим через В2, В3,..., Вn точки пересечения этой окружности с лучами ОА2, ОА3,..., ОАn. Построим, наконец, отрезки В1В2, В2В3,..., ВnВ1. Получим искомый правильный n-угольник В1В2...Вn.

Приближённые построения правильных многоугольников

Приближенное построение правильного пятиугольника способом
А. Дюрера.
Приближенное построение правильного пятиугольника представляет собой интерес. А.Дюрером оно проводится при условии неизменности раствора циркуля, что повышает точность построения. Способ построения описан Дюрером так:"Однако пятиугольник, построенный неизменным раствором циркуля, делай так. Проведи две окружности так, чтобы каждая из них проходила через центр другой. Два центра А и В соедини прямой линией. Это и будет стороной пятиугольника. Точки пересечения окружностей обозначь сверху С, снизу D и проведи прямую линию CD. После этого возьми циркуль с неизменным раствором и, установив одну его ножку в точку D, другой проведи через оба центра А и В дугу до пересечения её с обеими окружностями. Точки пересечения обозначь через E и F, а точку пересечения с прямой CD обозначь буквой G. Теперь проведи прямую линию через Е и G до пересечения с линией окружности. Эту точку обозначь Н. Затем проведи другую линию через F и G до пересечения с линией окружности и поставь здесь J.
Соединив J,A и H,B прямыми, получим три стороны пятиугольника. Дав возможность двум сторонам такой длины достигнуть совпадения в точке K из точек J и H, получим некоторый пятиугольник."

Построение правильного вписанного в окружность многоугольника с любым числом сторон.
Один из таких практических методов, позволяющий построить правильный вписанный в окружность многоугольник с любым числом сторон известен как приём Биона(рис.1).
Пусть дана окружность и АВ - её диаметр. Построим правильный треугольник АВС и разделим АВ‚ точкой D в отношении AD : AB =2 : n. Пусть продолжение CD пересечёт окружность в точке E. Тогда АЕ представляет сторону правильного вписанного n-угольника.(На рис.1 приведено построение стороны правильного семиугольника.) При n=5,7,9,10 погрешность построения не привышает 1%. С возрастанием n погрешность приближения растёт, но остаётся меньше 10,3%.
Среди различных подходов к построению правильных многоугольников выделяется задача на построение правильного многоугольника по данной стороне. Ещё в XV в. великий художник Леонардо да Винчи (1452-1519), занимаясь такими построениями, установил соотношение между стороной многоугольника и апофемой:
аn/2 : ha =3/(n-1)(рис.2), которое можно выразить так: tg180°/n =3/(n-1).

1888 г. в журнале " Вестник опытной физики и элементарной математики" появилась статья Ф. Коваржика, где он предложил общий способ построения правильных многоугольников по данной стороне (рис.3).
Пусть АВ- сторона правильного n-угольника, который требуется построить. На АВ строим равно
сторонний треугольник АВС, из точки С опускаем перпендикуляр CD на АВ и продолжаем его. Затем делим АВ на 6 равных частей и такие откладываем на СD по обе стороны от С. Точки деления являются центрами окружностей, описанных около искомых многоугольников. Перенумеровав эти точки, как показано на рисунке, получим, что, например, А7 - радиус окружности, описанной около семиугольника, сторона которого равна АВ.
Для шестиугольника и двенадцатиугольника такое построение даёт точный результат. Докажем, что для других значений n предложенное построение обладает достаточно высокой точностью. Пусть величина центрального угла ANB некоторого n-угольника равна х. Обозначим АВ через а. Тогда по
теореме Пифагора CD= а - (а/2) = а / 2 ,
NC=(n-6/)*а/6
tgx/2=AD:ND=AD:(NC+CD)=
=a/2:((n-6)* а /6 + а /2)=
= a/2 :( а /2 *((n-6):3 + ))=
= 1:(( n-6):3 + )=
=1:((n-6 +3 ):3 )= 3:(n-6+3 )=
=3:((n-1)+0,19615)
(Сравните с результатом Леонардо да Винчи.)
Рассмотрим пример. Так, при n=7 tg x/2 =3/6,19615. Тогда х/2= 25°50'6'' и х= 51°40'12'', а центральный угол для правильного семиугольника равен 51°25'43''.
Погрешность составляет:
0,56% для 15-угольника; 3% для 20-угольника; 14% для 30-угольника; 74% для 40-угольника.
Приближённые способы построения правильных многоугольников просты и удобны на практике, красивы и орнаментaльны.

Теорема Фалеса
И всё же существует единый способ построения правильного n-угольника, в основу которого положена известная вам теорема геометрии. После знакомства с этим способом вам необходимо назвать эту теорему.
Для построения многоугольника из 11 равных сторон проведем из точки А под острым углом к отрезку (диаметру) АВ, прямую линию. На ней циркулем-измерителем откладываем нужное число равных отрезков произвольной величины, в данном случае 11. Последнюю точку соединяем с точкой В. Из нечетных точек деления с помощью линейки и угольника проводим прямые, параллельные прямой 11В. Если провести через все точки, то поделим отрезок АВ на 11 равных частей.
Сейчас проведем дугу СД радиусом ВА до пересечения с горизонтальной осью. Из точек С и Д будем проводить через точки 1’, 3’,5’ и т.д. лучи до пересечения с окружностью. Соединяем полученные точки на окружности между собой, и таким образом, мы вписали в окружность правильный многоугольник. Какая теорема используется?
Теорема Фалеса.

Устройство для графического построения правильных многоугольников
Известно, что простого специального приспособления для графического построения правильных многоугольников с четным или нечетным количеством сторон не имеется. Но если построение правильных многоугольников с четным количеством сторон с применением простых инструментов - циркуля и линейки без делений - не вызывает особых затруднений, то построение правильных многоугольников с нечетным количеством сторон (например, 7 или 9 и более сторон) без специальных сложных устройств весьма затруднено и практически невозможно.
Предложено простое устройство для графического построения правильных многоугольников как с четным, так и нечетным количеством сторон.
Устройство (см.рисунок) представляет собой тонкую прозрачную или непрозрачную полимерную пластинку в виде полукруга с центром в точке Р. Основание полукруга представляет собой ровную линейку без делений. По внешней стороне полукруга с левой стороны нанесены риски с одним и тем же интервалом. Каждая риска обозначена цифрами от 1 до 35 (или кратными последней цифре, например 5, 10, 15 и т.д.). Расстояние между рисками выбрано по величине произвольно. Количество рисок на устройстве определяет максимальное количество сторон для построения правильного многоугольника.
С уменьшением расстояния между рисками возможно расположить по контуру полукруга большее количество рисок, что позволит строить правильные многоугольники с большим количеством сторон.
На правой стороне полукруга от точки В риской А отделена дуга величиной 60 градусов.

Графическое построение правильных многоугольников при помощи данного устройства производится следующим образом. Например, необходимо построить правильный 9-угольник. Для этого делают следующие шаги:
1. Проводят на листе бумаги горизонтальную линию.
2. Прикладывают полукруг сверху на проведенную линию и обводят по контуру полностью полукруг. После этого точками обозначают на листе бумаги риски с буквами Р, О, В, А, а также точки напротив рисок с цифрами 6 и 9.
3. Проводят линию между точками 6 и В.
4. Проводят два луча: один из точки Р через точку А, а второй - из точки 9 параллельно линии ОВ. Эти два луча пересекутся в точке, которую необходимо обозначить, например, буквой К.
5. Циркулем проводят полуокружность из точки М на линии ОВ так, чтобы эта полуокружность проходила через точки 9 и К. В этом случае точка М является точкой пересечения диаметра ОВ с перпендикуляром к середине отрезка, соединяющего точки 9 и К.
6. Проведенная циркулем полуокружность пересечет линию ОВ в точке Е, а ее продолжение за точку В - в точке Д, и, кроме того, она пересечет луч из точки В через точку 6 в точке С.
7. Циркулем откладывают на дуге КД дугу НД, равную дуге СЕ.
8. Проводят луч из точки Р через точку Н, который пересечет дугу АВ в точке Т. Величина дуги ВТ составит точно 1/9 часть окружности с центром в точке Р и радиусом РВ.
9. Откладывая на данной окружности девять размеров дуги ВТ и соединив соседние засечки отрезками, получают правильный 9-угольник, вписанный в окружность с центром в точке Р.
Точность графических построений зависит только от точности применяемых инструментов и тщательности выполняемых графических работ.

Проводят циркулем заданную окружность с центром в точке О произвольным радиусом, а затем проводят два взаимно перпендикулярных диаметра АВ и СД.
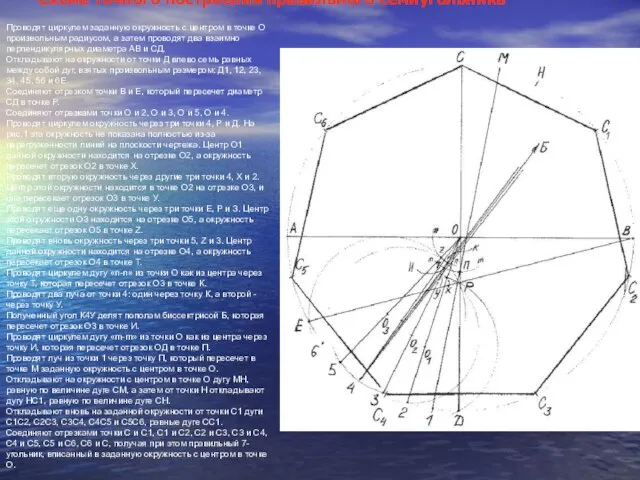
Откладывают на окружности от точки Д влево семь равных между собой дуг, взятых произвольным размером: Д1, 12, 23, 34, 45, 56 и 6Е.
Соединяют отрезком точки В и Е, который пересечет диаметр СД в точке Р.
Соединяют отрезками точки О и 2, О и 3, О и 5, О и 4.
Проводят циркулем окружность через три точки 4, Р и Д. На рис.1 эта окружность не показана полностью из-за перегруженности линий на плоскости чертежа. Центр О1 данной окружности находится на отрезке О2, а окружность пересечет отрезок О2 в точке Х.
Проводят вторую окружность через другие три точки 4, Х и 2. Центр этой окружности находится в точке О2 на отрезке О3, и она пересекает отрезок О3 в точке У.
Проводят еще одну окружность через три точки Е, Р и З. Центр этой окружности О3 находится на отрезке О5, а окружность пересекает отрезок О5 в точке Z.
Проводят вновь окружность через три точки 5, Z и 3. Центр данной окружности находится на отрезке О4, а окружность пересекает отрезок О4 в точке Т.
Проводят циркулем дугу «n-n» из точки О как из центра через точку Т, которая пересечет отрезок О3 в точке К.
Проводят два луча от точки 4: один через точку К, а второй - через точку У.
Полученный угол К4У делят пополам биссектрисой Б, которая пересечет отрезок О3 в точке И.
Проводят циркулем дугу «m-m» из точки О как из центра через точку И, которая пересечет отрезок ОД в точке П.
Проводят луч из точки 1 через точку П, который пересечет в точке М заданную окружность с центром в точке О.
Откладывают на окружности с центром в точке О дугу МН, равную по величине дуге СМ, а затем от точки Н откладывают дугу НС1, равную по величине дуге СН.
Откладывают вновь на заданной окружности от точки С1 дуги С1С2, С2С3, С3С4, С4С5 и С5С6, равные дуге СС1.
Соединяют отрезками точки С и С1, С1 и С2, С2 и С3, С3 и С4, С4 и С5, С5 и С6, С6 и С, получая при этом правильный 7-угольник, вписанный в заданную окружность с центром в точке О.
Схема точного построения правильного семиугольника

Схема построения взаиморавных больших и малых
радиальных дуг
Абсолютная точность данных геометрических построений подтверждается математическими выкладками, а производимая точность самих построений зависит во многом от тщательности работ и точности применяемых инструментов.
Действительно, в одном и том же круге равные между собой малые дуги «а» и «в» на его окружности при равных углах a при вершине своих секторов позволяют получить равные между собой большие дуги «А» и «В» на этой же окружности, а, следовательно, и разделить заданную дугу с сумой больших дуг на равные между собой части.

А так ли уж важно изучать и знать сведения о правильных многоугольниках? В каких житейских ситуациях можно встретиться с правильными многоугольниками?
Историческая справка.
В математике паркетом называют «замощение» плоскости повторяющимися фигурами без пропусков и перекрытий. Простейшие паркеты были открыты пифагорейцами около 2500 лет тому назад. Они установили, что вокруг одной точки могут лежать либо шесть правильных многоугольников (3600: 600 = 6), либо четыре квадрата (3600: 900 = 4), либо три правильных шестиугольника (3600: 1200 = 3), так как сумма углов с вершиной этой точки равна 3600. Вы не задумывались вот над таким вопросом: Почему пчелы «выбрали» себе для ячеек на сотах форму правильного шестиугольника?
Пчелы – удивительные творения природы. Свои геометрические способности они проявляют при построении своих сот. Если возьмем равносторонний треугольник, квадрат и правильный шестиугольник одинаковой площади (показываю модели), то периметр шестиугольника будет наименьшим. (Р3 = 45,9 см., Р4 = 40 см., Р6 = 37,8 см.).
Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек.
Причем пчелиные соты представляют собой не плоский, а пространственный паркет, поскольку заполняют пространство так, что не остается просветов.
И как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».

Петропавловская крепость

Платоновы тела
Платоновы тела - трехмерный аналог плоских правильных многоугольников.
Существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида.
Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды
.Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.

Многогранники в искусстве

Работы Эшера

Правильные геометрические тела - многогранники - имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов
Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона. Это - тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

"Порядок и хаос".
Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду. Для преобразования многогранника в звезду необходимо заменить каждую его грань пирамидой, основанием которой является грань многогранника. Изящный пример звездчатого додекаэдра можно найти в работе "Порядок и хаос". В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором.
Заметим также, что анализируя картину можно догадаться о природе источника света для всей композиции - это окно, которое отражается левой верхней части сферы.

Гравюра "Звезды"
Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра "Звезды", на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.