Презентация на тему Преобразование плоскости

ДВИЖЕНИЯ
Образуют специальный класс преобразований,
играющих особую роль в различных науках и их приложениях
и широко распространенных в области природных и технических явлений

ДВИЖЕНИЕ
или
ПЕРЕМЕЩЕНИЕ
- это преобразование плоскости,
сохраняющее расстояния

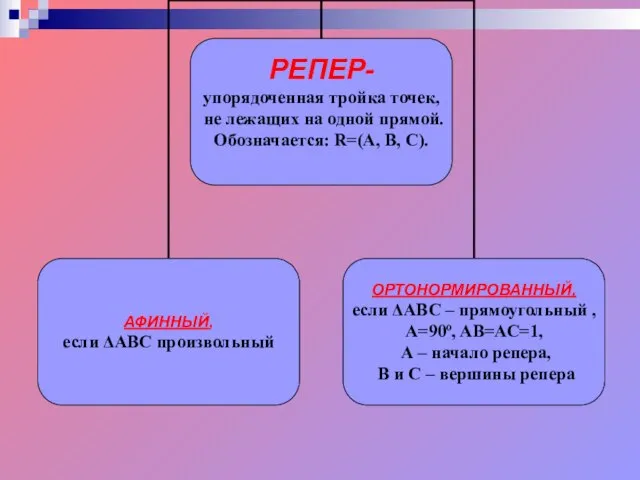
При движении репер R, образованный точками A, В, С, переходит в репер R', образованный точками A', B', C', причем это движение единственно.
А
В
С
R:
A'
B'
C'
R' :

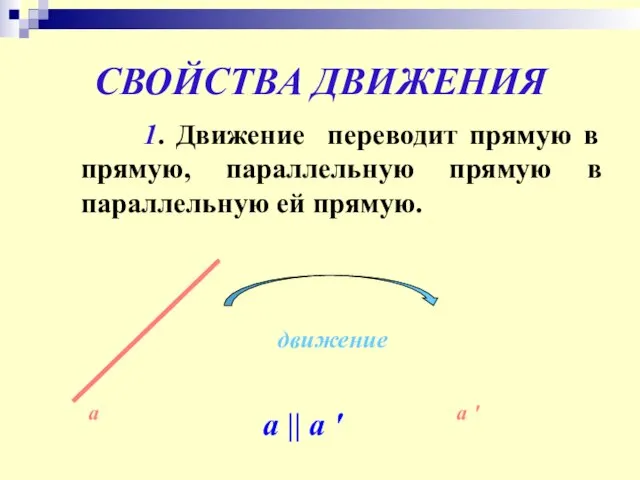
СВОЙСТВА ДВИЖЕНИЯ
1. Движение переводит прямую в прямую, параллельную прямую в параллельную ей прямую.
а
движение
а '
а || а '

СВОЙСТВА ДВИЖЕНИЯ
2. Движение переводит полуплоскость с границей A в полуплоскость c границей А', где А' – образ прямой a.
а
a’
Образ прямой а

СВОЙСТВА ДВИЖЕНИЯ
3. Движение сохраняет простое отношение трех точек прямой.
А
В
С
λ
=AC : CB
A1
B1
C1
λ1=A1C1 : C1B1
λ =λ 1

СВОЙСТВА ДВИЖЕНИЯ
4. Движение сохраняет отношение «лежать между».
5. Движение переводит отрезок AB в отрезок A'B'. При этом середина отрезка AB переходит в середину отрезка A'B'.

СВОЙСТВА ДВИЖЕНИЯ
6. Движение переводит угол в равный ему угол,
луч в луч
A
A1
A=
A1
А
М
А '
М '
АМ
А'М'

СВОЙСТВА ДВИЖЕНИЯ
7. Движение переводит взаимно перпендикулярные прямые во взаимно перпендикулярные прямые
а
b
a'
b'
движение

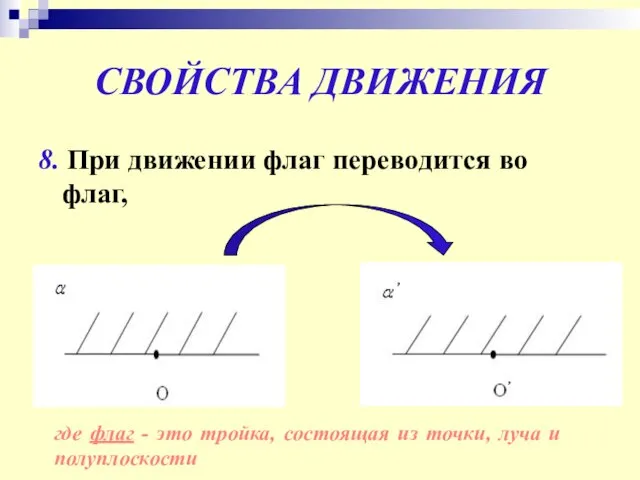
СВОЙСТВА ДВИЖЕНИЯ
8. При движении флаг переводится во флаг,
где флаг - это тройка, состоящая из точки, луча и полуплоскости

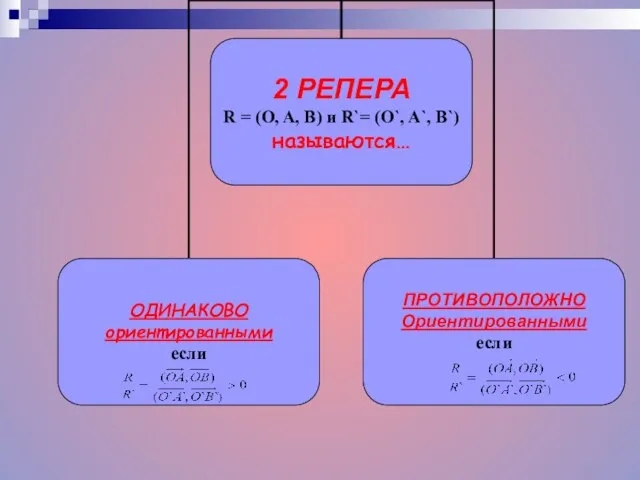
Преобразование точек плоскости сохраняет ориентацию плоскости или меняет ориентацию плоскости,
если любой репер и его образ
сохраняют или меняют ориентацию

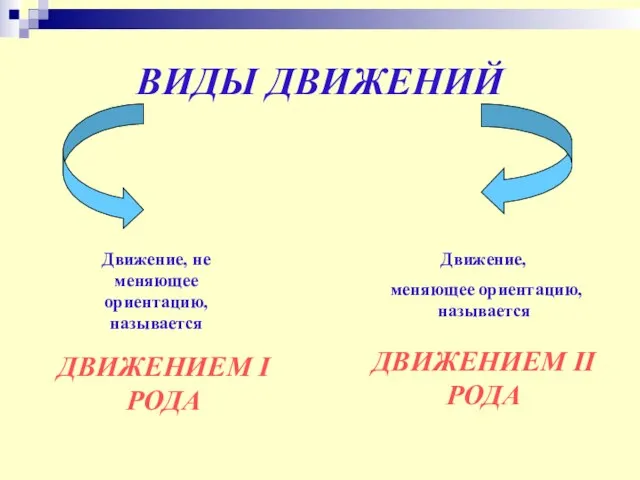
ВИДЫ ДВИЖЕНИЙ
Движение, не меняющее ориентацию, называется
ДВИЖЕНИЕМ I РОДА
Движение,
меняющее ориентацию, называется
ДВИЖЕНИЕМ II РОДА

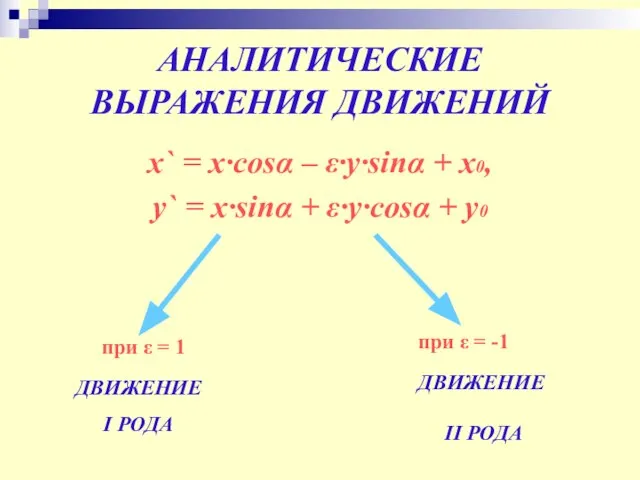
АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДВИЖЕНИЙ
x` = x∙cosα – ε∙y∙sinα + x0,
y` = x∙sinα + ε∙y∙cosα + y0
при ε = 1
ДВИЖЕНИЕ
I РОДА
при ε = -1
ДВИЖЕНИЕ
II РОДА

ДВИЖЕНИЕ I РОДА
1. Поворот на угол
А
М
М1
Аналитические выражения:
x` = x∙cosα – y∙sinα ,
y` = x∙sinα + y∙cosα
а) тождественное преобразование,
б) центральная симметрия,
x` = x
y` = y
x` =- x+х0
y` =- y+y0

ДВИЖЕНИЕ I РОДА
2. а)Параллельный перенос на
Аналитические выражения:
x` = x+х0
y` =y
б) Параллельный перенос на
- тождественное преобразование
x
y

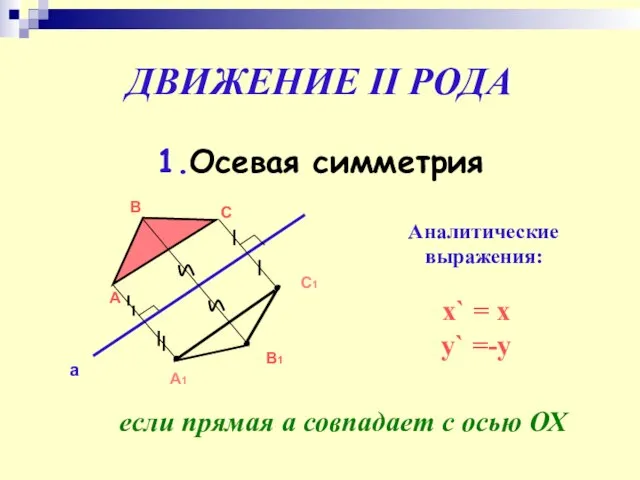
ДВИЖЕНИЕ II РОДА
1.Осевая симметрия
А
В
С
а
С1
А1
В1
Аналитические выражения:
x` = x
y` =-y
если прямая а совпадает с осью ОХ

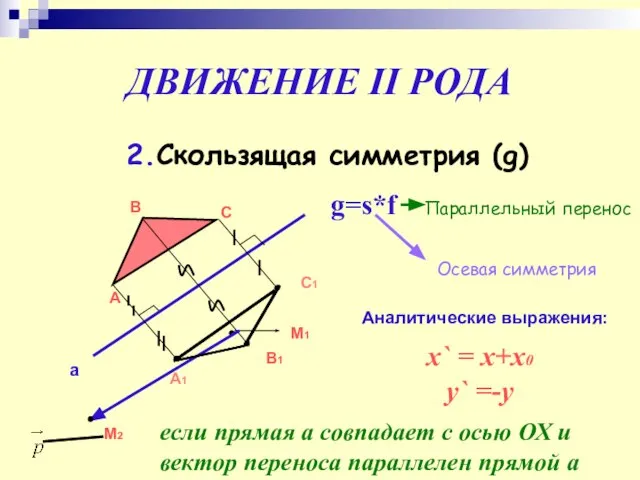
ДВИЖЕНИЕ II РОДА
2.Скользящая симметрия (g)
А
В
С
а
С1
А1
В1
g=s*f
Осевая симметрия
Параллельный перенос
М1
М2
Аналитические выражения:
x` = x+x0
y` =-y
если прямая а совпадает с осью ОХ и вектор переноса параллелен прямой а

ПРЕОБРАЗОВАНИЕ
ПОДОБИЯ
Преобразование плоскости называется преобразованием подобия, если существует k > 0, такое что для любых точек A, B, A`, B` выполняется равенство:
A`B` = kAB
При k =1 преобразование подобия является движением

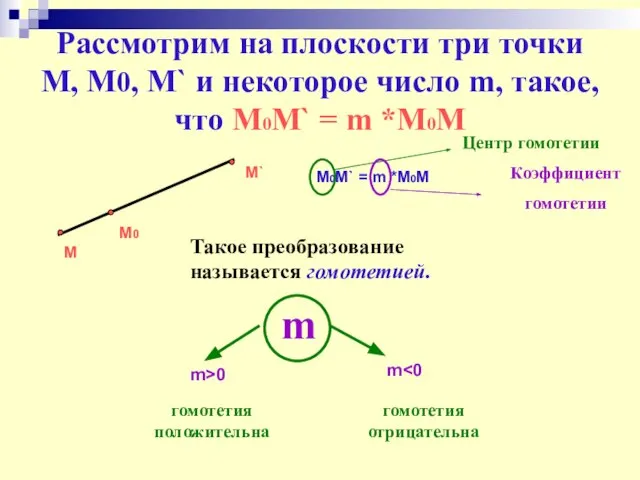
Рассмотрим на плоскости три точки М, М0, M` и некоторое число m, такое, что М0M` = m *М0M
М0
М
M`
М0M` = m *М0M
Такое преобразование называется гомотетией.
Центр гомотетии
Коэффициент
гомотетии
m
m>0
гомотетия положительна
m<0
гомотетия отрицательна

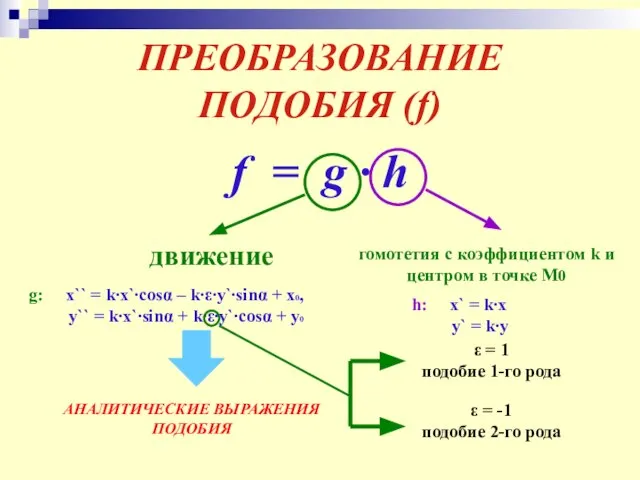
ПРЕОБРАЗОВАНИЕ
ПОДОБИЯ (f)
f = g ∙ h
движение
гомотетия с коэффициентом k и центром в точке М0
h: x` = k∙x
y` = k∙y
g: x`` = k∙x`∙cosα – k∙ε∙y`∙sinα + x0,
y`` = k∙x`∙sinα + k∙ε∙y`∙cosα + y0
АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ПОДОБИЯ
ε = 1
подобие 1-го рода
ε = -1
подобие 2-го рода

ПОДОБИЕ I РОДА
Аналитические выражения:
x` = k∙x∙cosα – k∙y∙sinα + x, y` = k∙y∙sinα + k∙y∙cosα + y
1. Поворот на угол
а) тождественное преобразование, если
б) центрально-подобное вращение, если
в) центрально-подобная симметрия

2. Параллельный перенос на
О
О1
Аналитические выражения:
x` = k∙x+ x0,
y` = k∙y+ y0

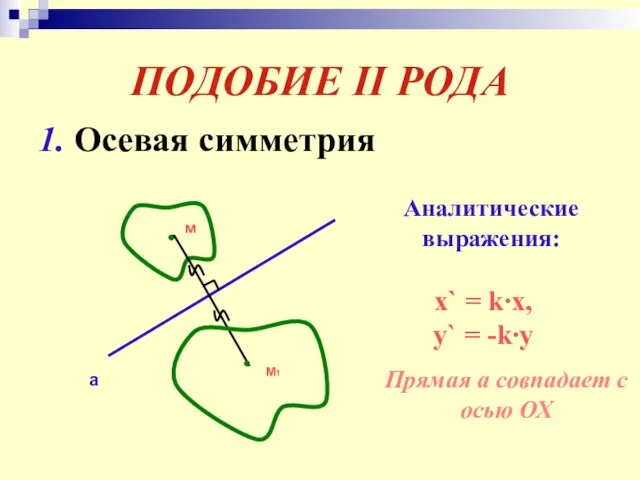
ПОДОБИЕ II РОДА
1. Осевая симметрия
м
а
М1
Аналитические выражения:
x` = k∙x,
y` = -k∙y
Прямая а совпадает с осью ОХ

ПОДОБИЕ II РОДА
2. Скользящая симметрия
x
y
М
М1
М’
Аналитические выражения:
x` = k∙x+x0,
y` = -k∙y

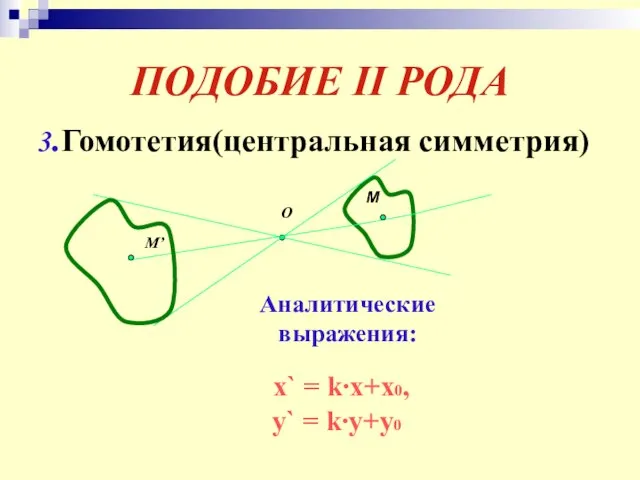
ПОДОБИЕ II РОДА
3.Гомотетия(центральная симметрия)
О
М
М’
Аналитические выражения:
x` = k∙x+x0,
y` = k∙y+y0