Презентация на тему Термодинамика Второе и третье начало термодинамики

8.8. Круговой процесс (цикл)
Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное.
Процессы: расширения (1—2), сжатия (2—1) .
Работа расширения положительна и определяется площадью фигуры (dV>0).
Работа сжатия отрицательна (dV<0).
Цикл, совершаемый идеальным газом:

Прямой цикл используется в тепловых двигателях — периодически действующих двигателях, совершающих работу за счет полученной извне теплоты.
Обратный цикл используется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой.
В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю.
Поэтому первое начало термодинамики для кругового процесса:
Если за цикл совершается положительная работа, то он называется прямым.

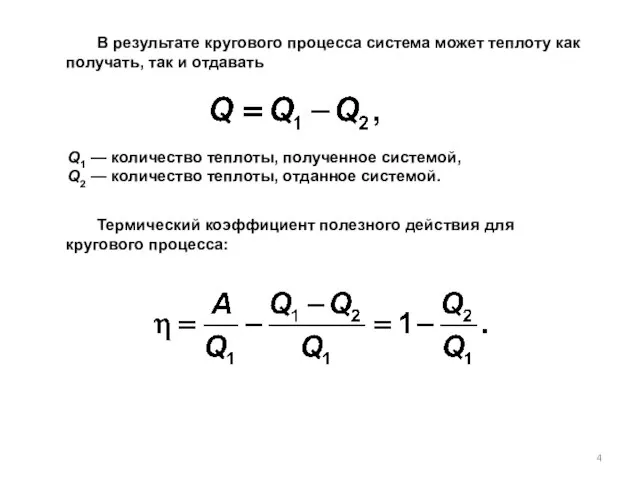
В результате кругового процесса система может теплоту как получать, так и отдавать
Q1 — количество теплоты, полученное системой,
Q2 — количество теплоты, отданное системой.
Термический коэффициент полезного действия для кругового процесса:

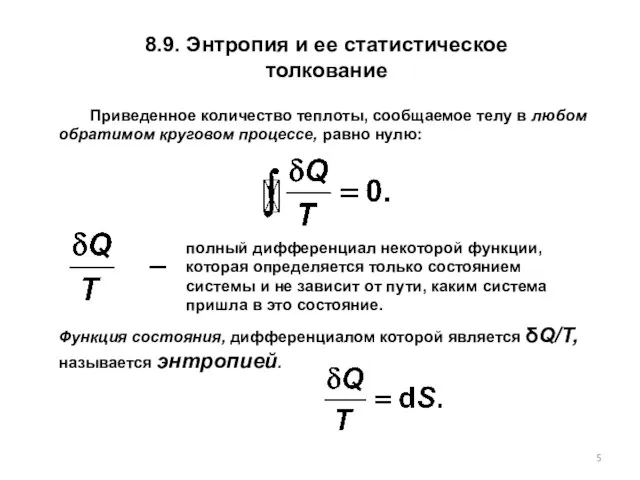
8.9. Энтропия и ее статистическое толкование
Приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю:
полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние.
Функция состояния, дифференциалом которой является δQ/T, называется энтропией.

Для обратимых процессов изменение энтропии:
Для системы, которая обменивается теплотой с внешней средой, энтропия может быть:
Для необратимых процессов изменение энтропии:
- неравенство Клаузиуса.
Энтропия замкнутой системы может либо возрастать, либо оставаться постоянной.

Если система совершает равновесный переход из состояния 1 в состояние 2, то изменение ее энтропии:

или
Замечания:
Изменение энтропии ΔS1→2 идеального газа при переходе его из состояния 1 в со­стояние 2 не зависит от вида процесса перехода 1 → 2.
Адиабатический обратимый процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом.
Изменение энтропии в процессах идеального газа:

Изменение энтропии при изотермическом процессе:
Изменение энтропии при изохорном процессе:
Следствия для приращения энтропии:

Термодинамическая вероятность состояния системы — это число микросостояний, определяющих данное макросостояние.
Энтропия системы и термодинамическая вероятность связаны между собой следующим выражением:
k — постоянная Больцмана.
- формула Больцмана,
Связь энтропии с термодинамической вероятностью.
Энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние.
Энтропия – мера вероятности состояния термодинамической системы.

Статистическое толкование энтропии на основе формулы Больцмана:
«энтропия является мерой неупорядо­ченности системы (мерой хаоса)».
Другое определение энтропии.
Замечания:
Энтропия и термодинамичес­кая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процес­сов).
Все процессы в реальной замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии.

8.10. Второе начало термодинамики
Второе начало термодинамики определяет направление протекания термодинамических процессов. «В замкнутой системе при необратимых процессах энтропия системы возрастает».
Возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния.
Еще две формулировки второго начала термодинамики:
по Кельвину:
невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу,
2) по Клаузиусу:
невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

В середине XIX в. возникла проблема так называемой тепловой смерти Вселенной.
Рассматривая Вселенную как замкнутую систему и применяя к ней второе качало термодинамики, Клаузиус свел его содержание к утверждению, что энтропия Вселенной должна достигнуть своего максимума.
Это означает, что со временем все формы движения должны перейти в тепловую. Переход же теплоты от горячих тел к холодным приведет к тому, что температура всех тел во Вселенной сравняется, т. е. наступит полное тепловое равновесие и все процессы во Вселенной прекратятся — наступит тепловая смерть Вселенной.

8.11. Третье начало термодинамики
Теорема Нернста — Планка:
«энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина»:
Вальтер Нернст (1864 - 1941) — немецкий химик.
Макс Планк (1858 - 1947) — немецкий физик.

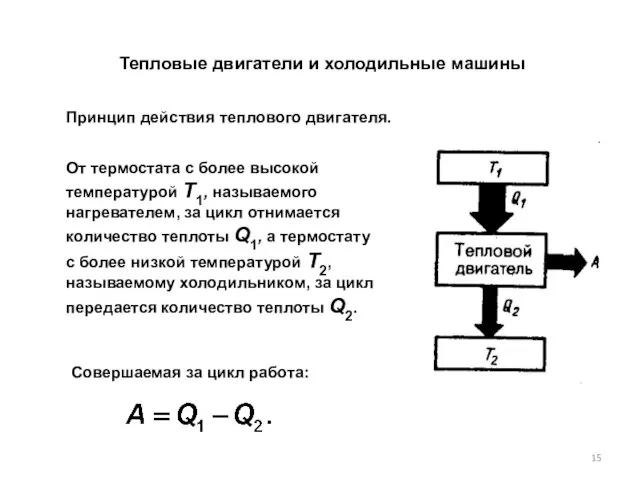
Тепловые двигатели и холодильные машины
От термостата с более высокой температурой Т1, называемого нагревателем, за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой Т2, называемому холодильником, за цикл передается количество теплоты Q2.
Принцип действия теплового двигателя.
Совершаемая за цикл работа:

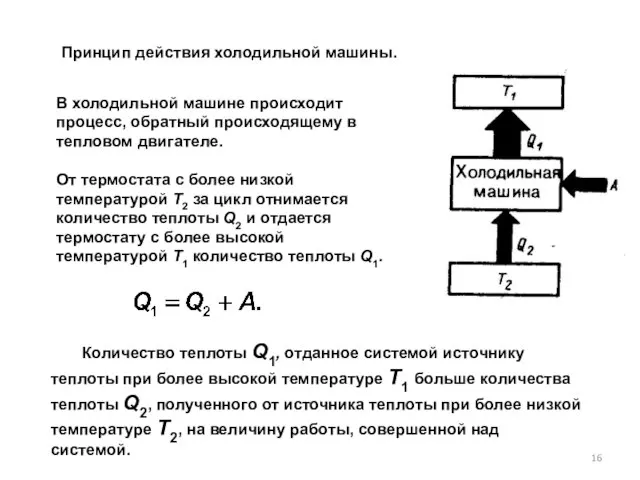
В холодильной машине происходит процесс, обратный происходящему в тепловом двигателе.
От термостата с более низкой температурой Т2 за цикл отнимается количество теплоты Q2 и отдается термостату с более высокой температурой Т1 количество теплоты Q1.
Принцип действия холодильной машины.
Количество теплоты Q1, отданное системой источнику теплоты при более высокой температуре T1 больше количества теплоты Q2, полученного от источника теплоты при более низкой температуре T2, на величину работы, совершенной над системой.

Теорема Карно:
«из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (T1) и холодильников (T2), наибольшим к. п. д. обладают обратимые машины».
Карно теоретически проанализировал обратимый наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат. Его называют циклом Карно.
Цикл Карно для идеального газа
Садии Карно (1796 - 1832 ) — французский физик и математик.

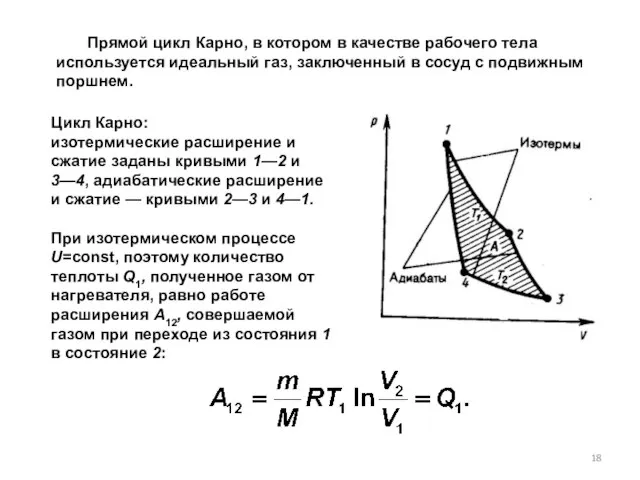
Цикл Карно:
изотермические расширение и сжатие заданы кривыми 1—2 и
3—4, адиабатические расширение и сжатие — кривыми 2—3 и 4—1.
При изотермическом процессе U=const, поэтому количество теплоты Q1, полученное газом от нагревателя, равно работе расширения А12, совершаемой газом при переходе из состояния 1 в состояние 2:
Прямой цикл Карно, в котором в качестве рабочего тела используется идеальный газ, заключенный в сосуд с подвижным поршнем.

При адиабатическом расширении 2—3 теплообмен с окружающей средой отсутствует и работа расширения А23 совершается за счет изменения внутренней энергии
Количество теплоты Q2, отданное газом холодильнику при изотермическом сжатии, равно работе сжатия А34:
Работа адиабатического сжатия: