Презентация тв и мс мфпа

Рекомендуемая литература
«Теория вероятностей и математическая статистика»
под редакцией Мхитаряна В.С.

Применение математической статистики
Статистические методы успешно применяются в различных отраслях народного хозяйства, практически во всех областях науки: анализ издержек и прибыли предприятий, оценка зависимости между показателями экономических объектов при разных уровнях неопределенности, построение математико-статистических моделей на основе принципа максимальной согласованности и др.
Затраты на статистический анализ данных в России оцениваются примерно в 2 миллиарда рублей ежегодно.

Элементы теории вероятностей
События
Классификация
Вероятность события
Теоремы сложения и умножения
Формулы полной вероятности и Баейеса
Схема повторных испытаний Бернулли
2. Случайные величины
Дискретные и непрерывные
Статистические характеристики
Предельные теоремы теории вероятностей
Закон больших чисел: лемма Маркова, неравенство и теорема Чебышева, теоремы Бернулли и Пуассона
Центральная предельная теорема

Математическая статистика
Статистическая оценка параметров
Точечные оценки
Интервальные оценки
2. Проверка статистических гипотез
О неизвестном законе распределения
О неизвестных параметрах известного закона распределения
О равенстве параметров
3. Изучение взаимозависимости показателей
Корреляционный анализ
Регрессионный анализ

Событие – любой факт, который может произойти в результате опыта (испытания)
Опыт (испытание) – осуществление определенного комплекса условий
Классификация:
совместные и несовместные
Достоверные и невозможные
Зависимые и независимые
Случайные
Равновозможные
Полная группа событий

Вероятность события – численная мера степени объективной возможности появления события
Классическая вероятность:
Р(А)=m/n, где
m – число благоприятствующих исходов,
n – общее число исходов опыта.
Статистическая вероятность:
Р(А)=m/n, где
m – абсолютная частота появления события,
n – число проведенных испытаний.
Используется свойство устойчивости частот.

Свойства вероятности:
Изменяется в пределах от «0» до «1»
Вероятность достоверного события = 1
Вероятность невозможного события = 0
Вероятность полной группы событий = 1
Сложные события:
Понятие суммы и произведения событий
Р(А+В), А или В
Р(А*В), А и В

Теоремы сложения:
для совместных событий
Р(А+В)=Р(А)+Р(В)-Р(А*В)
для несовместных событий
Р(А+В)=Р(А)+Р(В)
Теоремы умножения:
для зависимых событий
Р(А*В)=Р(А)*Р(В)/А
Р(А*В)=Р(В)*Р(А)/В
для независимых событий
Р(А*В)=Р(А)*Р(В)

Формула полной вероятности:
Р(А)= Σ (Р(Вi)*Р(А)/Вi), где
i = 1,2,3,…n
Р(Вi) – априорные вероятности гипотез
Формула Байеса:
Р(Bj/A) = (Р(Вj)*Р(А)/Вj) / Р(А)
Р(Bj/A) – апостериорные вероятности гипотез
Событие А не может произойти без гипотез
В1, В2, В3,…Вn

Схема повторных испытаний Бернулли:
n – не велико, формула Бернулли
Рn,m = Cnm pm qn-m
n – велико, локальная теорема Лапласа
Рn,m = ƒ(t) /(npq)0,5 , где ƒ(t) –плотность нормированного нормального распределения;
t =(m-np)/(npq)0,5
n – велико, Р – мало, формула Пуассона
Рn,m = λm e-λ /m!, где λ=np
m!=1*2*3…*m
Сnm= n!/m!(n-m)!

Случайная величина, в отличие от события, является колличественной характеристикой результатов испытания
Дискретная случайная величина принимает конечное множество значений
Непрерывная случайная величина может принимать любые значения из некоторого конечного или бесконечного интервала
Случайная величина подчиняется закону распределения
Закон распределения – всякое соответствие между возможными значениями случайной величины и соответствующими им вероятностями

Закон распределения дискретной случайной величины может представлен в виде таблицы:
Закон распределения непрерывной случайной величины представляют с помощью интегральной и дифференциальной функций:
F(x) – интегральная функция
f(x) – дифференциальная функция
F'(x) = f(x)

Функция распределения
Является наиболее общей формой задания закона распределения случайной величины, ее используют как для дискретных, так и для непрерывных случайных величин.
Она определяет вероятность того, что случайная величина не превысит некоторого фиксированного значения

Свойства функции распределения
Для дискретных случайных величин функция распределения имеет скачок в точках, где она принимает конкретные значения. В интервалах между значениями она постоянна. Сумма всех скачков функции распределения равна единице. График- разрывная ступенчатая ломаная линия.

Свойства функции распределения
Для непрерывной случайной величины функция распределения является непрерывной и имеет график плавной кривой
Функция распределения является неотрицательной, т.е. ее значения заключены между нулем и единицей

Свойства функции распределения
Вероятность попадания случайной величины в интервал равна разности значений функции распределения на концах этого интервала
Функция распределения является неубывающей
Каждая случайная величина однозначно определяет функцию распределения, а одну и ту же функцию распределения могут иметь различные случайные величины

Теоретические законы распределения случайных величин:
нормальный закон распределения
распределение Пирсона
распределение Стьюдента распределение Фишера-Снедекора
G – распределение
равномерное распределение
биномиальное распределение

Нормальный закон распределения
Правило «трех сигм»
Характеристики положения равны
Характеристики формы ряда распределения равны нулю
В силу действия закона больших чисел встречается чаще других теоретических законов

Числовые характеристики случайных величин:
М(х) - математическое ожидание
Д(х) - дисперсия
Мо - мода
Ме - медиана
μк; νк – центральные и начальные моменты различных порядков
Математическое ожидание, мода, медиана представляют значения случайной величины, вокруг которых происходит вариация
Дисперсия характеризует степень отклонения случайной величины от математического ожидания

Свойства математического ожидания

Свойства дисперсии

Другие законы распределения
Биномиальный
Распределение Пуассона
Равномерный закон распределения
Распределение Стьюдента
F- распределение

Предельные теоремы теории вероятностей
Закон больших чисел составляет ряд теорем, посвященных вопросам приближения некоторых случайных величин к определенным предельным значениям независимо от их закона распределения (лемма Маркова, неравенство Чебышева, теоремы Чебышева, Маркова, Бернулли, Пуассона)
Центральная предельная теорема посвящена предельным законам распределения суммы случайных величин с учетом различных условий, накладываемых на сумму составляющих (впервые доказана великим русским статистиком А.М.Ляпуновым)

Интегральная теорема Муавра-Лапласа
Частным случаем центральной предельной теоремы является интегральная теорема Муавра-Лапласа. Речь идет о вероятности попадания случайной величины в заданный интервал
Рассматриваются ситуации, когда случайная величина имеет биномиальное распределение, нормальное, Стьюдента, Пирсона, Фишера-Снедекора

Математическая статистика
Статистическая совокупность – совокупность однородных единиц, обладающих качественной общностью и различающихся колличественно
Генеральная статистическая совокупность включает все единицы изучаемого процесса
Выборочная совокупность включает небольшое количество единиц генеральной совокупности и обладает репрезентативностью, т.е. отражает все свойства и пропорции генеральной совокупности

Математическая статистика изучает закономерность массовых явлений
Закон отражает объективную связь между явлением и причиной, характеризует результат конкретного опыта
Закономерность определяет средний результат большого числа испытаний и не характеризует результат конкретного опыта

Математическая статистика разрабатывает методы регистрации описания и анализа статистических данных, полученных в результате наблюдения массовых явлений
Задачи математической статистики начинаются там , где по результатам выборочных наблюдений надо судить о всей генеральной совокупности
Теория вероятностей позволяет оценить степень точности полученных результатов

Задачи математической статистики
Определение законов распределения наблюдаемых величин
Оценка неизвестных параметров законов распределения
Проверка статистических гипотез относительно распределений изучаемых величин
Анализ взаимозависимости показателей

Анализ вариации
Вариация – изменчивость величин при переходе от одного элемента статистической совокупности к другому
Различают вариацию: дискретную, непрерывную, атрибутивную
Вариант – значение отдельного элемента совокупности
Частота показывает сколько раз наблюдается отдельный элемент совокупности

Графическое изображение вариационных рядов
Полигон
Гистограмма
Кумулята
Огива
Построение графиков для непрерывной и дискретной вариации имеет свои особенности

Статистические характеристики
Положения: средние, мода, медиана
Меры вариации: размах вариации, дисперсия, среднее квадратическое отклонение, среднее линейное отклонение, коэффициент вариации
Характеристики формы ряда распределения: коэффициент асимметрии, эксцесс

Моменты: характер распределения может быть выявлен с помощью небольшого числа моментов
Начальные моменты: средняя арифметическая – начальный момент первого порядка
Центральные моменты: дисперсия – центральный момент второго порядка, коэффициент асимметрии и эксцесс – модифицированные центральные моменты третьего и четвертого порядков

Процедура выявления закона распределения
Задача: по результатам выборки определить закон распределения изучаемой величины
Предварительный анализ включает расчет статистических характеристик, построение эмпирических графиков, сравнение со свойствами теоретического закона
Проверка гипотезы о неизвестном законе распределения с помощью критериев согласия

Нормальный закон распределения
Х N(μ;σ)
Равенство характеристик положения
Правило «3σ»

Статистическая оценка параметров
Методы статистического оценивания:
метод максимального правдоподобия
метод наименьших квадратов
метод моментов
Точечные оценки параметров нормального закона распределения:
Математическое ожидание – средняя арифметическая
Дисперсия – выборочная дисперсия

Метод максимального правдоподобия
Функция правдоподобия рассматривается как вероятность совместного появления результатов выборки (Х1,Х2, …, Хn)
Статистические оценки параметров наиболее правдоподобно отражающие значения параметров теоретического распределения максимизируют функцию правдоподобия
Оценки максимального правдоподобия находят решением системы «к» уравнений, где к – число оцениваемых параметров

Метод моментов
Заключается в приравнивании определенного количества «к» выборочных моментов соответствующим теоретическим, где к – число оцениваемых параметров
Оценки параметров являются решением системы уравнений
ММ на практике используется для получения первого приближения оценки с последующим уточнением
ММ привлекателен простотой вычислительной реализации

Метод наименьших квадратов
На практике применяется при построении регрессионных моделей
В основе метода лежит минимизация суммы квадратов отклонений теоретических и эмпирических значений исследуемого признака
Для линейных моделей позволяет получать состоятельные, асимптотически несмещенные, нормальные и эффективные оценки

Свойства точечных оценок:
несмещенность – математическое ожидание оценки равно самому параметру М(Qn)=Q эффективность – минимальная дисперсия оценки
состоятельность – асимптотическое выполнение несмещенности и эффективности при безграничном увеличении объема выборки
Точность точечных оценок увеличивается при увеличении объема выборки
Для получения более точных оценок при малых объемах выборки рассчитывают интервальные оценки

При малых объемах выборки интервальная оценка является более точной
Интервальная оценка – некоторый интервал, относительно которого с вероятностью близкой к единице можно утверждать, что оцениваемый параметр находится внутри него.

Интервальные оценки параметров нормального закона распределения
Р(Q*-δ< Q < Q*+δ)= γ, где
Q – оцениваемый параметр
Q*- точечная оценка параметра
δ – точность оценки
γ - надежность оценки
Математическое ожидание μ :
при известной дисперсии σ2
дисперсия не известна
Дисперсия σ2:
объем выборки меньше 30
объем выборки больше 30

Распределение некоторых статистик
Решение практических задач, связанных с малыми выборками, требует знания точных законов распределения выборочных характеристик.
Если выборка сделана из нормальной совокупности, то средняя арифметическая, рассчитанная по этой выборке тоже имеет нормальное распределение.

Распределение разности средних величин
Если выборка сделана из двух нормальных совокупностей, то разность средних величин этих совокупностей тоже будет подчиняться нормальному закону.

Распределение Пирсона
Если Х1,Х2,…,Хк - ряд независимых нормированных нормально распределенных случайных величин, то сумма квадратов этих величин будет подчиняться распределению Пирсона с числом степеней свободы «к».
«к» - единственный параметр распределения Пирсона, характеризующий число независимых слагаемых

Оценки параметров нормальной совокупности
Доказано, что в случае нормальной выборки средняя арифметическая и выборочная дисперсия взаимно независимы
средняя арифметическая подчиняется нормальному закону, а дисперсия имеет распределение Пирсона с числом степеней свободы «n-1»

Распределение Стьюдента
(t – распределение)
Если Z и U взаимно независимые случайные величины, соответственно подчиняющиеся нормированному нормальному закону и распределению Пирсона, то величина представляющая собой отношение Z/U будет иметь распределение Стьюдента.

Распределение Фишера-Снедекора
(F – распределение)
Отношение двух взаимно независимых случайных величин, имеющих распределение Пирсона соответственно со степенями свободы К1 и К2, будет подчиняться распределению Фишера - Снедекора со степенями свободы К1 и К2.
Статистики, имеющие F – распределение, по своему значению не бывают меньше единицы.

Асимптотические распределения
Доказано, что распределения Стьюдента, Пирсона и Фишера – Снедекора не очень требовательны к выполнению гипотезы о нормальном распределении и следовательно соответствующие статистики можно использовать при достаточно больших объемах выборки и не строгом выполнении требований относительно нормальности распределения
Нет однозначного ответа на вопрос об объеме выборки, при котором выборочную характеристику можно считать распределенной нормально

Проверка статистических гипотез
Статистическая гипотеза – всякое предположение либо относительно неизвестного закона распределения, либо относительно неизвестных параметров известного закона распределения
Процедура проверки статистической гипотезы:
выдвигается Н0 – нулевая гипотеза, которую следует проверить
подбирается Н1- альтернативная гипотеза, которая будет верна если не верна нулевая
выбирают уровень значимости α

подбирают критерий для проверки гипотезы, основу которого составляет статистика с известным законом распределения при справедливости нулевой гипотезы
в зависимости от альтернативной гипотезы выбирают тип критической области
определяют границу критической области
рассчитывают наблюдаемое значение статистики критерия
если наблюдаемое значение статистики попадает в критическую область, то считают, что нулевая гипотеза противоречит опытным данным

Уровень значимости α – вероятность совершить ошибку первого рода (α+γ=1)
β - вероятность совершить ошибку второго рода
(1- β) – мощность критерия, вероятность не совершить ошибку второго рода

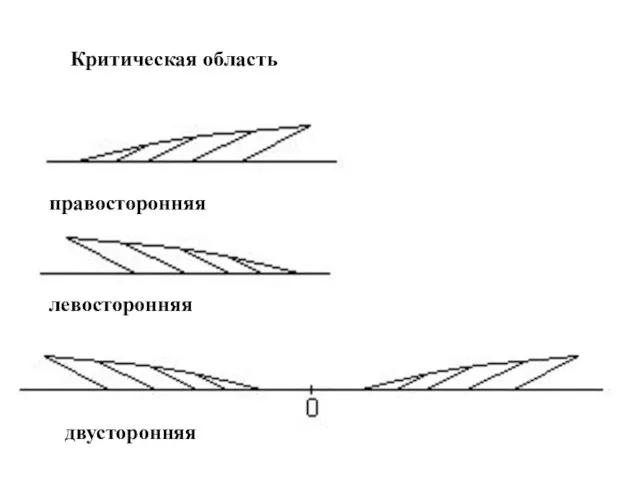
Критическая область
правосторонняя
левосторонняя
двусторонняя

Требования,
предъявляемые к критической области:
статистика должна принадлежать критической области с минимальной вероятностью (α), если верна нулевая гипотеза Н0
статистика должна принадлежать критической области с максимальной вероятностью (1- β), если верна альтернативная гипотеза Н1
Желание минимизировать вероятности ошибок первого и второго рода приводит к необходимости выбора рекомендуемых уровней значимости:
0,005 0,001 0,05 0,01

Проверка гипотез о значении параметров нормального закона распределения
Н0:μ= μ0 при известной дисперсии σ2
Н1: μ= μ1 μ1< μ0, левосторонняя,
μ1 > μ0, правосторонняя
Н1: μ= μ0 , двусторонняя
Н0: μ= μ0
Н1: μ= μ1 дисперсия не известна
Н0: σ2= σ02 σ12 < σ02 , левосторонняя,
Н1: σ2= σ12 σ12 > σ02 , правосторонняя
Н1: σ2= σ02, двусторонняя

Проверка гипотезы об однородности ряда дисперсий
Н0: σ12= σ22 = σ32=…= σk2
Критерий Кохрана, если n1=n2=n3= …=nk
Критерий Бартлета, если n1=n2=n3= …=nk
Проверка гипотезы о равенстве параметров:
Н0: μ1= μ2, при известной и неизвестной дисперсии
Н0: σ12= σ22 , проверяется только при правосторонней критической области

Проверка гипотезы о нормальном законе распределения
Н0: Х N(μ;σ)
Используются критерии согласия:
Пирсона Романовского
Ястремского
Условия применения критерия Пирсона:
объем выборки не менее 50 единиц
каждый интервал содержит не менее 5 вариантов
если есть интервалы с частотой менее 5, то их присоединяют к близлежащим интервалам, а частоты складывают

Изучение взаимозависимости между показателями
Корреляционная зависимость – зависимость среднего значения результативного признака У от значений факторов Хi
Задачи корреляционного анализа:
Определить наличие корреляционной связи
оценить тесноту связи
проверить значимость параметров связи
для значимых параметров связи рассчитать доверительные интервалы

Анализ двумерной линейной модели
Для определения наличия корреляционной зависимости строят поле корреляции.
По характеру расположения точек поля оценивают характер связи между изучаемыми показателями: положительная (прямая), отрицательная (обратная)

Анализ двумерной линейной модели
Теснота связи оценивается с помощью парного линейного коэффициента корреляции. Следует различать значение коэффициента в генеральной совокупности и его оценку по выборке
Для оценки тесноты связи надо знать свойства парного линейного коэффициента корреляции

Анализ двумерной линейной модели
Параметрами связи модели являются: парный линейный коэффициент корреляции и два коэффициента регрессии
Связь между ними позволяет свести процедуру проверки значимости параметров связи к проверки значимости только коэффициента корреляции

Анализ двумерной линейной модели
Для значимых параметров связи целесообразно провести расчет доверительных интервалов
В процедуре расчета доверительного интервала для парного линейного коэффициента корреляции участвует статистика Z – преобразования Фишера

Анализ двумерной линейной модели
На практике анализ двумерной модели рассматривают в двух случаях: когда исходные данные представлены в виде рядов наблюдения и в виде корреляционной таблицы
Для двумерной линейной модели на практике задачи корреляционного и регрессионного анализа не разделяют

Задачи регрессионного анализа
Определить характер связи: линейный, нелинейный
На практике наиболее предпочтительна собственно линейная модель
Ŷ=b0+b1X1+b2X2+ …+bkXk
Оценить параметры регрессионной модели
Используется метод наименьших квадратов
Проверить значимость модели
Проверить значимость коэффициентов модели
Выбрать модели для практического использования среди статистически надежных
Дать экономическую интерпретацию модели

Анализ двумерной линейной модели
В рамках двумерной линейной модели задачи регрессионного анализа сводятся к оценке параметров модели, проверке значимости модели и расчета доверительного интервала для условной средней
Метод наименьших квадратов не всегда применяется для оценки параметров модели

Ранговая корреляция
Для изучения взаимосвязи признаков, не поддающихся количественному измерению, используются различные показатели ранговой корреляции.
Элементы совокупности ранжируют, каждому объекту присваивают порядковый номер – ранг.

Ранговая корреляция
Наиболее часто на практике используют коэффициенты ранговой корреляции :
Спирмэна;
Кэндела;
Конкордации;
Ассоциации;
Контингенции и др.

Трехмерная модель
В рамках трехмерной модели задачи изучения взаимосвязи между показателями усложняются:
Задачи корреляционного и регрессионного анализа рассматривают отдельно;
Оценивают девять параметров корреляционной модели (три математических ожидания, три дисперсии, три парных линейных коэффициентов корреляции);
Для оценки тесноты связи используют парные , частные, множественные коэффициенты корреляции.

ПРИМЕНЕНИЕ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА В ЭКОНОМИЧЕСКИХ ИССЛЕДОВАНИЯХ
У - результативный признак, случайная величина зависящая от факторов Хj (j=1,2,…к).
Хj - факторы, определяющие вариацию У.
Матрица исходных данных( n>>k)
У1 Х11 Х 12 Х 13 ……………….. Х1к
У2 Х21 Х22 Х23 ……………….. Х2к
………………………………………………………..
Уn Хn1 Хn2 Хn3 ………………. Хnк

ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ
1. Расчет вариационных характеристик факторов, включаемых в модель.
2. Анализ значений вариационных характеристик факторов: коэффициентов асимметрии и эксцесса, средней арифметической, моды, медианы, дисперсии.
3. Проверка гипотезы о нормальности распределения факторов.
4. Вывод о включении в модель отдельных факторов.

Корреляционный анализ
1. Анализ матрицы парных коэффициентов.
2. Проверка значимости связи результативного признака с факторами.
3. Анализ модели на мультиколлинеарность.
4. Определение мультиколлинеарных пар факторов в модели.
5. Разработка рекомендаций по выбору факторов, включаемых в модель.

Анализ матрицы парных коэффициентов корреляции
Y X1 X2 X3 X4 X5
Y 1 r1 r2 r3 r4 r5
X1 1 r12 r13 r14 r15
X2 1 r23 r24 r25
X3 1 r34 r35
X4 1 r45
X5 1

ПРОВЕРКА ЗНАЧИМОСТИ КОРРЕЛЯЦИОННОЙ
ЗАВИСИМОСТИ РЕЗУЛЬТАТИВНОГО ПРИЗНАКА С ФАКТОРАМИ
Н0: rj=0 α=0,005,
если rjнабл.> rкр.(α=0,005; ν = n-2), то гипотеза отвергается, следовательно результативный признак имеет значимую связь с данным фактором.
Гипотеза Н0: rj=0 проверяется для j= 1- К, в данном примере К=5.

АНАЛИЗ МОДЕЛИ НА МУЛЬТИКОЛЛИНЕАРНОСТЬ
Если в матрице парных коэффициентов корреляции
имеются значения / rij / > 0,8, то пара факторов с индексами i,j является мультиколлинеарной.
Линейная зависимость между компонентами матрицы Х называется мультиколлинеарностью аргументов регрессии, которая вызывает неустойчивость оценок коэффициентов регрессии, большие дисперсии и коэффициенты корреляции этих оценок.

РАЗРАБОТКА РЕКОМЕНДАЦИЙ ПО ВЫБОРУ ФАКТОРОВ, ВКЛЮЧАЕМЫХ В МОДЕЛЬ
- В модель следует включать факторы, имеющие значимую корреляционную связь с результативным признаком.
- Для построения статистически устойчивой модели нельзя включать одновременно факторы, имеющие тесную линейную зависимость.
- Использовать метод пошаговой регрессии для последовательного включения факторов в модель.
- Использовать матрицу частных коэффициентов корреляции для оценки значимости корреляционной связи освобожденной от влияния третьих факторов.

РЕГРЕССИОННЫЙ АНАЛИЗ
1. Регрессионную модель можно считать статистически надежной, если она является значимой со всеми значимыми коэффициентами.
2. Собственно линейная регрессионная модель:
У = β0+ β1Х1+ β2Х2+…+ βкХк
3. Проверка значимости уравнения регрессии.
4. Проверка значимости коэффициентов уравнения регрессии.
5. Использование критерия Дарбина-Уотсона для оцени автокорреляции.

Проверка значимости уравнения регрессии
Предполагается, что в генеральной совокуцпности все коэффициенты модели равны нулю
Н0: β=0 α=0,005, если
вектор β= β0 равен нулю, то модель
β1
.
βк
незначима.
Fнабл = QR(n-k-1)/Qост(k+1)>Fкр(α=0,005; ν1= k+1;ν2= n-k-1)
Используется таблица F-распределения.

Проверка значимости коэффициентов уравнения регрессии
Основу критерия, используемого для проверки значимости коэффициентов регрессии составляет статистика:
Fнабл=b2j/Ŝ2bj, где
b2j – оценка коэффициента;
Ŝ2bj – исправленная дисперсия коэффициента.
Для проверки гипотезы Н0: βj =0, по таблице F-распределения находят Fкр(α; ν1=1;ν2= n-k-1)

Анализ наличия автокорреляции в модели
Для решения проблем автокорреляции в регрессионном анализе используют критерий Дарбина-Уотсона. Основу критерия составляет статистика d, которая меняет свои значения в пределах от 0 до 4:
d=0 соответствует сильной обратной автокорреляции;
d=2 означает отсутствие автокорреляции;
d=4 указывает на сильную положительную автокорреляцию

Экономическая интерпретация модели
Статистически надежная модель рекомендуемая для практического использования имеет экономическую интерпретацию. Коэффициент стоящий при факторе показывает на сколько единиц меняется значение результативного признака при увеличении на единицу фактора.
Экономическая интерпретация модели – рекомендации заказчику по использованию регрессионной модели для решения практических задач.

ЗАДАЧИ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА
1. Измерение тесноты корреляционной зависимости.
2. Отбор факторов наиболее существенно связанных с результативным признаком.
3. Анализ причин и характера взаимозависимости факторов (положительный, отрицательный).
4. Установление формы зависимости (линейная, нелинейная; парная, множественная, частная).
5. Выбор функции регрессии.
6. Статистическая оценка параметров модели.
7. Анализ типа соединения явлений (непосредственная, косвенная, ложная.

Проблемы изучения взаимозависимости показателей:
выполнение главной предпосылки – нормальность многомерной совокупности
мультиколлинеарность – тесная линейная связь между компонентами матрицы Х
автокорреляция – линейная связь между последовательными или сдвинутыми на лаг-τ уровнями фактора Хj
обеспечение статистической однородности матрицы исходных данных
используется кластерный анализ
снижение размерности матрицы исходных данных
используется метод главных компонент

Нелинейная парная корреляция
Использование корреляционного отношения основано на разложении общей дисперсии зависимой переменной на составляющие: дисперсию, характеризующую влияние объясняющей переменной, и дисперсию, характеризующую влияние неучтенных и случайных факторов