Применение множественной регрессии при решении экономических задач Белоглазова Юлия, ДС-01 МЭ

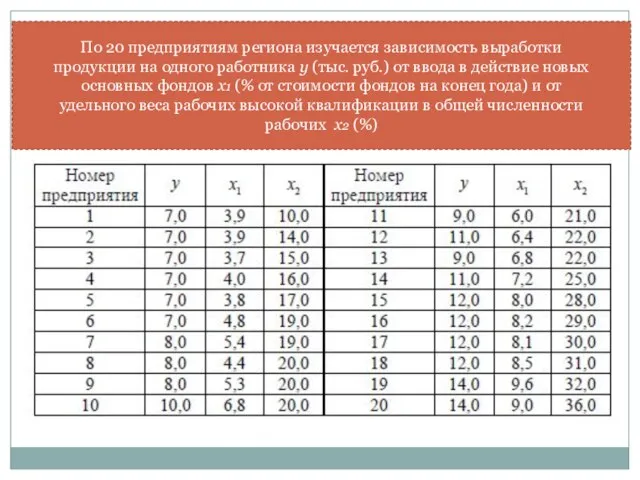
По 20 предприятиям региона изучается зависимость выработки
продукции на одного работника y (тыс. руб.) от ввода в действие новых
основных фондов x1 (% от стоимости фондов на конец года) и от
удельного веса рабочих высокой квалификации в общей численности
рабочих x2 (%)

Требуется:
Построить линейную модель множественной регрессии. Ранжировать факторы по степени их влияния на результат
Найти коэффициенты парной, частной и множестенной корреляции. Проанализировать их.
Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.
С помощью F -критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации
С помощью t -критерия оценить статистическую значимость коэффициентов чистой регрессии.
С помощью частных F -критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора x1 после x2 и фактора x2 после x1 .
Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.

Найдем средние квадратические отклонения
1

Найдем параметры линейного уравнения множественной регрессии
Коэффициенты корреляции
Параметры

Уравнение множественной регрессии
При увеличении ввода в действие основных фондов на 1% (при неизменном уровне удельного веса рабочих высокой квалификации) выработка продукции на одного рабочего увеличивается в среднем на 0,946 тыс. руб
При увеличении удельного веса рабочих высокой квалификации в общей численности рабочих на 1% (при неизменном уровне ввода в действие новых основных фондов) выработка продукции на одного рабочего увеличивается в среднем на 0,086 тыс. руб.

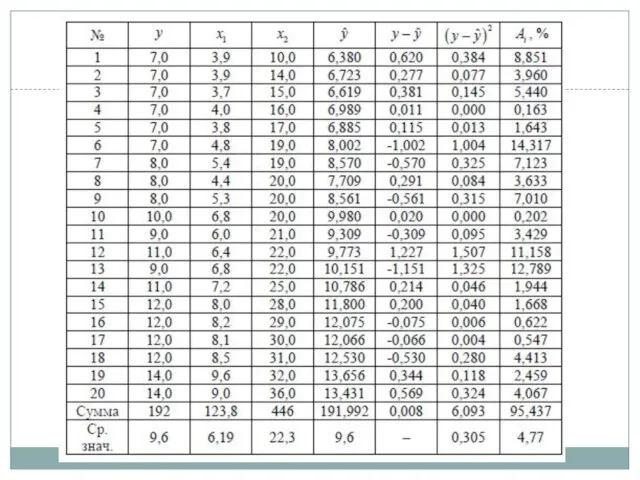
Результаты
Качество модели, исходя из относительных отклонений по каждому наблюдению, признается хорошим, т.к. средняя ошибка аппроксимации не превышает 10%
Введение в действие основных фондов влияет на результат больше, чем увеличение числа рабочих высокой квалификации

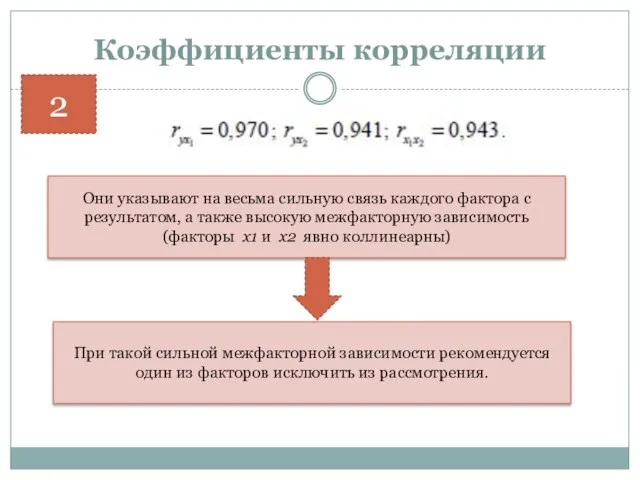
Коэффициенты корреляции
2
Они указывают на весьма сильную связь каждого фактора с
результатом, а также высокую межфакторную зависимость (факторы x1 и x2 явно коллинеарны)
При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения.

Частные коэффициенты корреляции
Если сравнить коэффициенты парной и частной корреляции, то
можно увидеть, что из-за высокой межфакторной зависимости
коэффициенты парной корреляции дают завышенные оценки тесноты связи.

Коэффициент множественной корреляции
Коэффициент множественной корреляции указывает на весьма
сильную связь всего набора факторов с результатом.

Коэффициент множественной детерминации
3
Скорректированный коэффициент множественной детерминации
Нескорректированный коэффициент множественной детерминации
Оба коэффициента указывают на весьма высокую (более 94%) детерминированность результата y в модели
факторами x1 и 2 x .

F -критерий Фишера
4
Подтверждается статистическая значимость всего уравнения
и показателя тесноты связи – к-та детерминации

t -критерий
5
Стандартные ошибки коэффициентов регрессии
Табличное значение критерия при уровне значимости a = 0,05 и
числе степеней свободы k =17 составит 2,11.
Таким образом, признается статистическая значимость параметра b1 и случайная природа формирования параметра b2

Частные F -критерии Фишера
6
Следовательно, включение в модель фактора x2 после того, как в модель
включен фактор x1 статистически нецелесообразно: прирост факторной
дисперсии за счет дополнительного признака x2 оказывается
незначительным