Применение производной

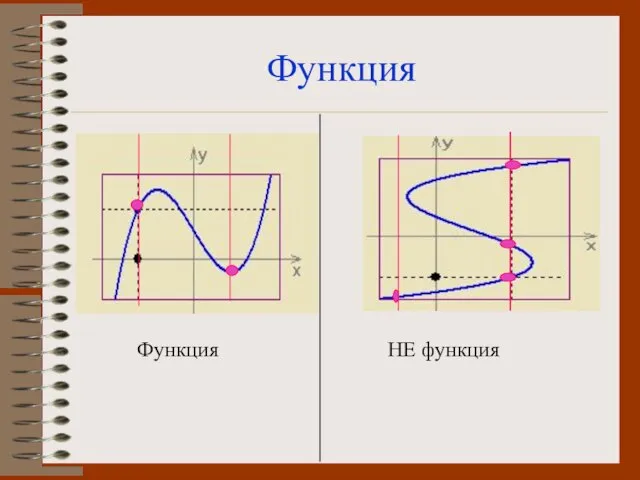
Функция
Функция
НЕ функция

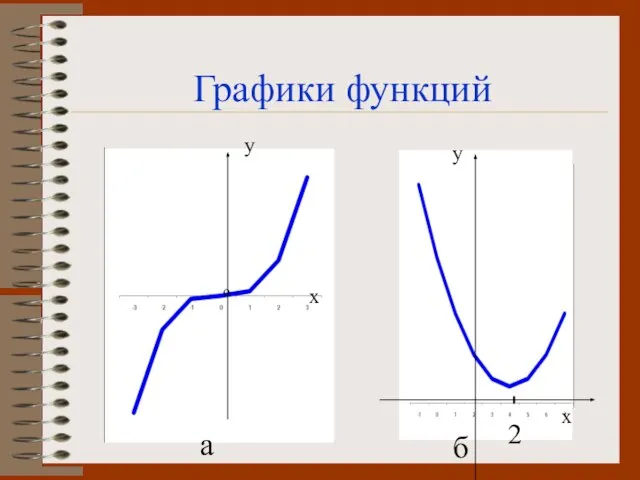
у
а
б
2
Графики функций

Возрастание и убывание функции
Иду в гору. Функция возрастает на промежутке[b;a]
Иду под гору. Функция убывает на промежутке[a;с]

Найдите производную функции:
f(x)=3x³-2x²-3x+5
f(x)=2x²+4x-4
f(x)=sinx
f(x)=sin2x
f(x)=√x
f(x)=2cosx
f(x)=cosx+10

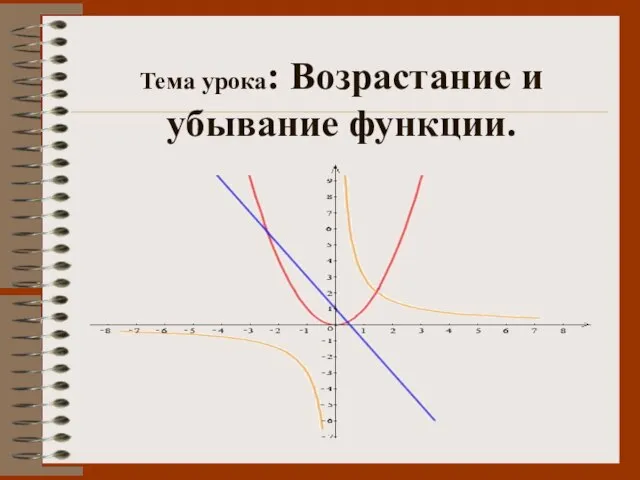
Тема урока: Возрастание и убывание функции.

Слушаю – забываю.
Смотрю – запоминаю.
Делаю – понимаю.
Конфуций

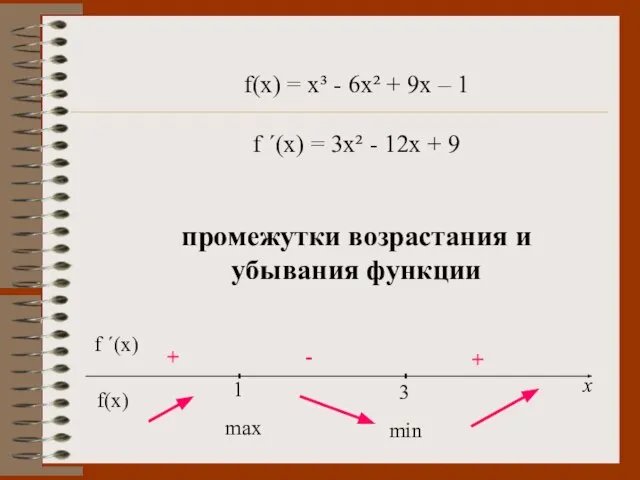
f(x)=x³ - 6x² + 9x – 1
f ´(x) = 3x² - 12x + 9
Найдем критические точки:
f ´(x) = 0, 3x² - 12x + 9 = 0
x² - 4x + 3 = 0
x = 1 и х = 3
х
1
3

Теорема: f(x) – непрерывна на I и имеет f ´(x)
а) f ´(x) > 0, то f(x) – возрастает
б) f ´(x) ˂ 0, то f(x) – убывает
в) f ´(x) = 0, то f(x) – постоянна(константа)

Доказательство:

f(x) = x³ - 6x² + 9x – 1
f ´(x) = 3x² - 12x + 9
Найдем критические точки:
f ´(x) = 0, 3x² - 12x + 9 = 0
x² - 4x + 3 = 0
x = 1 и х = 3
f ´(x) > 0, x ϵ (-∞; 1) и (3; + ∞)
f ´(x) ˂ 0, х ϵ (1; 3)

f(x) = x³ - 6x² + 9x – 1
f ´(x) = 3x² - 12x + 9
промежутки возрастания и убывания функции
х
f ´(x)
f(x)
1
3
+
-
+
max
min

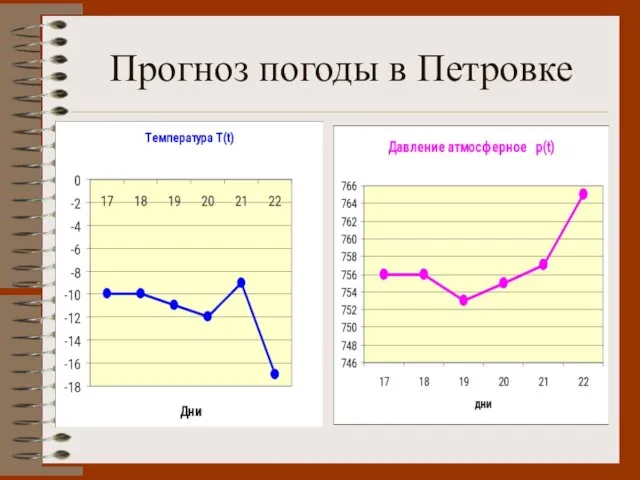
Прогноз погоды в Петровке

- обратиться к справочному материалу;
- обратиться учебнику;
- проанализировать выполнение аналогичных заданий;
- составить собственные примеры;
- обратиться за помощью к учителю.
План действий по локализации индивидуальных затруднений

Домашнее задание:
п.5.5,
№ 5.52б,
№ 5.53б,
№ 5.57б,
№ 5.58б.

К высотам познанья!
За кручей обрыв!
Дороги орлам незнакомы.
Пройдет человек лишь,
Но прежде открыв
Природы и чисел законы.
Искателей истин судьба нелегка,
Но тень их достанет в веках облака