Призма

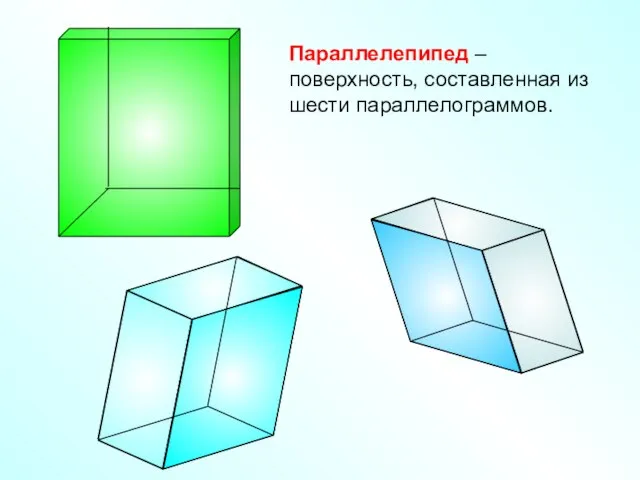
Параллелепипед – поверхность, составленная из шести параллелограммов.

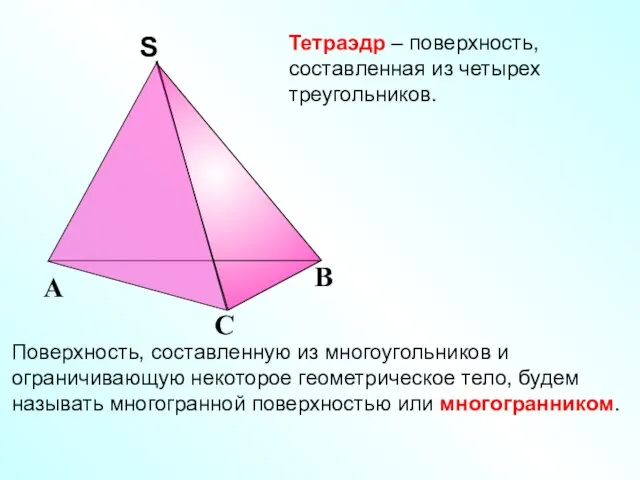
Тетраэдр – поверхность, составленная из четырех треугольников.
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.

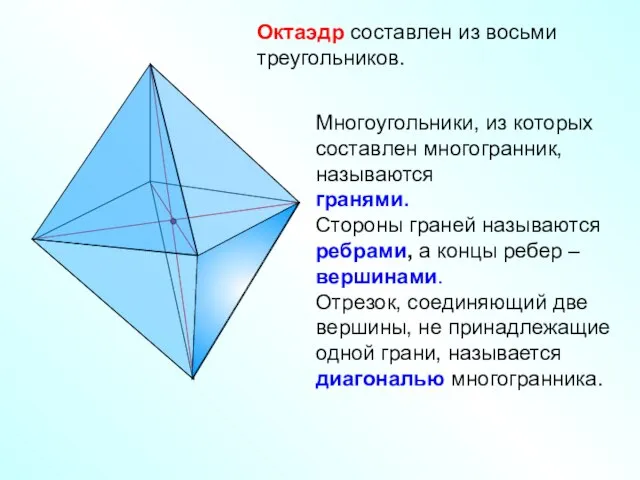
Октаэдр составлен из восьми треугольников.
Многоугольники, из которых составлен многогранник, называются
гранями.
Стороны граней называются ребрами, а концы ребер – вершинами.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

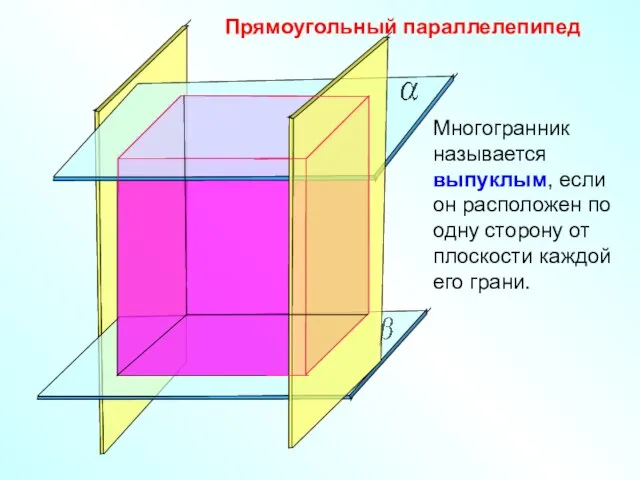
Прямоугольный параллелепипед
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

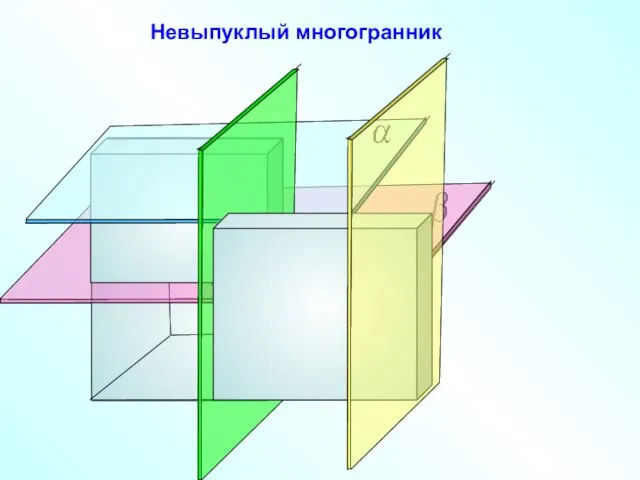
Невыпуклый многогранник

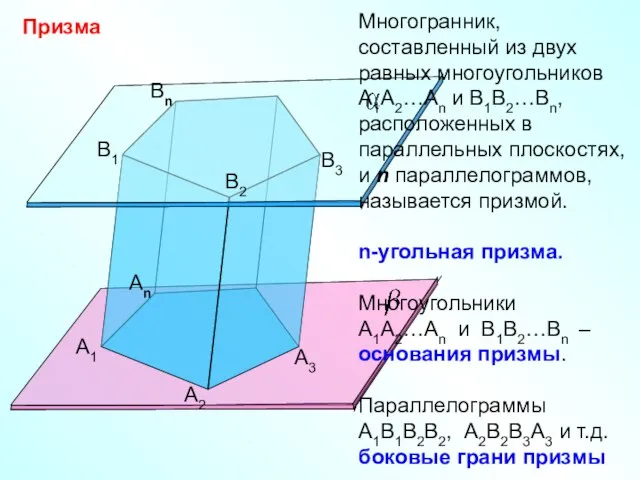
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.
n-угольная призма.
Многоугольники
А1А2…Аn и В1В2…Вn – основания призмы.
Параллелограммы А1В1В2В2, А2В2В3А3 и т.д. боковые грани призмы

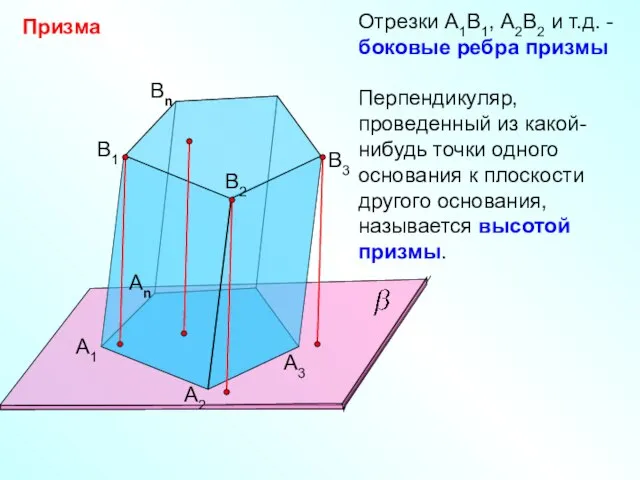
Призма
А1
А2
Аn
B1
B2
Bn
B3
А3
Отрезки А1В1, А2В2 и т.д. -
боковые ребра призмы
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

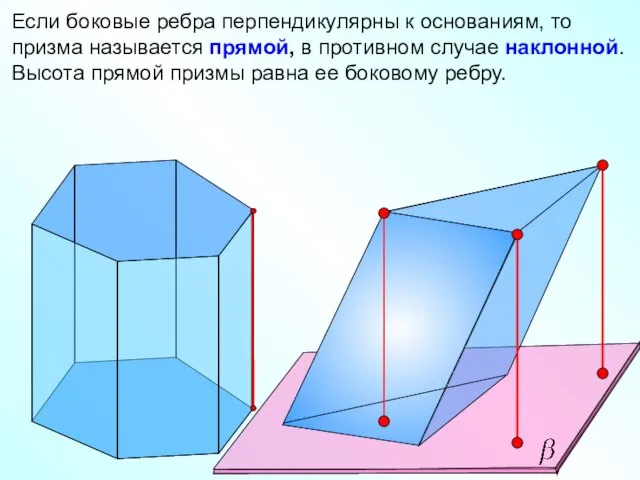
Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.

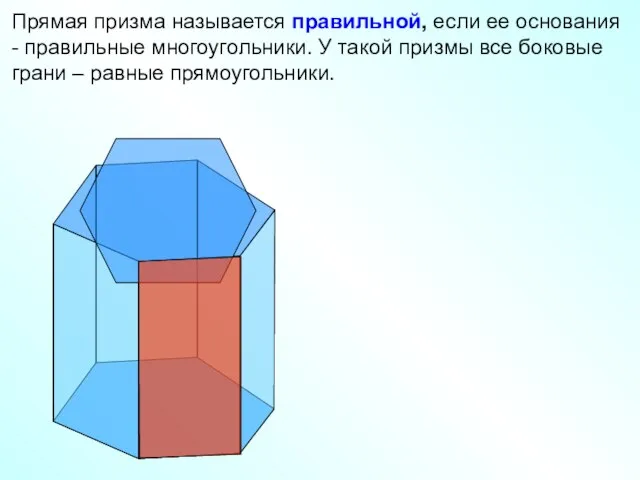
Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

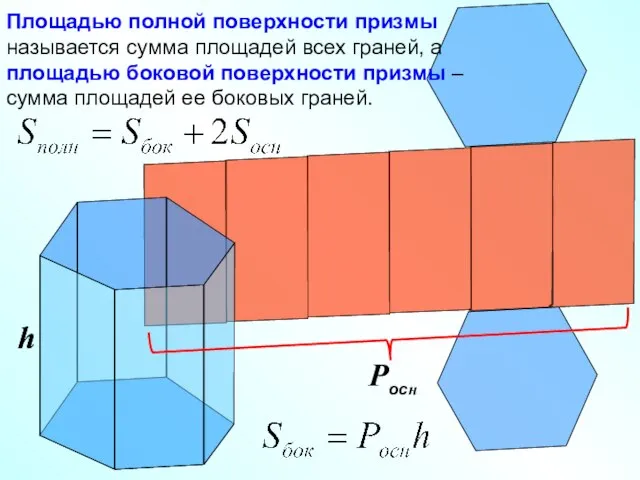
Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.
h
h
Pocн

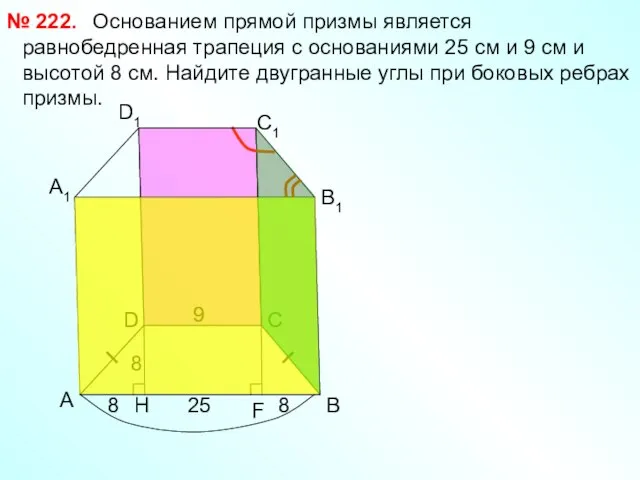
Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых ребрах призмы.
№ 222.
25
9
8
H
В
С
D
А1
D1
С1
В1
А
9

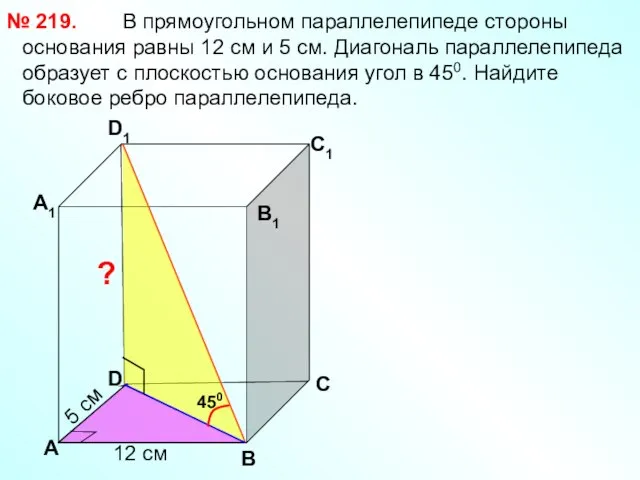
В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.
№ 219.
В
С
А1
D1
С1
В1
?
D
А
12 см
5 см

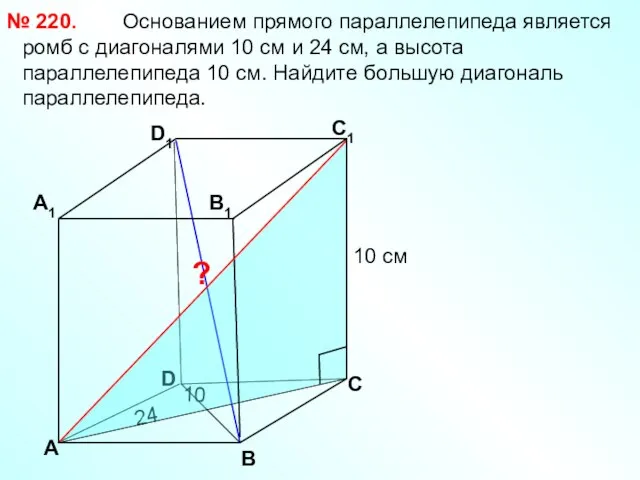
Основанием прямого параллелепипеда является ромб с диагоналями 10 см и 24 см, а высота параллелепипеда 10 см. Найдите большую диагональ параллелепипеда.
№ 220.
В
С
А1
D1
С1
В1
?
D
А
24
10
10 см

1. Сторона основания правильной треугольной призмы равна 8 см, а диагональ боковой грани равна 10 см. Найдите площадь боковой и полной поверхности призмы.
2. Основание прямой призмы – параллелограмм со сторонами 8 и 15 см и углом 120о. Боковая поверхность призмы имеет площадь 460 см2. Найдите площадь сечения призмы, проходящего через боковое ребро и меньшую диагональ основания.
3. Основание прямой призмы – прямоугольный треугольник с катетами 13 и 12 см. Меньшая боковая грань и основание призмы равновелики. Найдите площадь боковой и полной поверхности призмы.

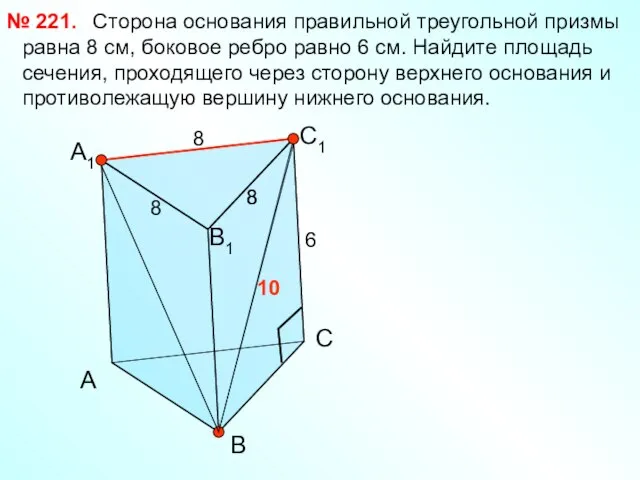
Сторона основания правильной треугольной призмы равна 8 см, боковое ребро равно 6 см. Найдите площадь сечения, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
№ 221.
А
В
С
С1
В1
А1
8
6
8
8
8
10

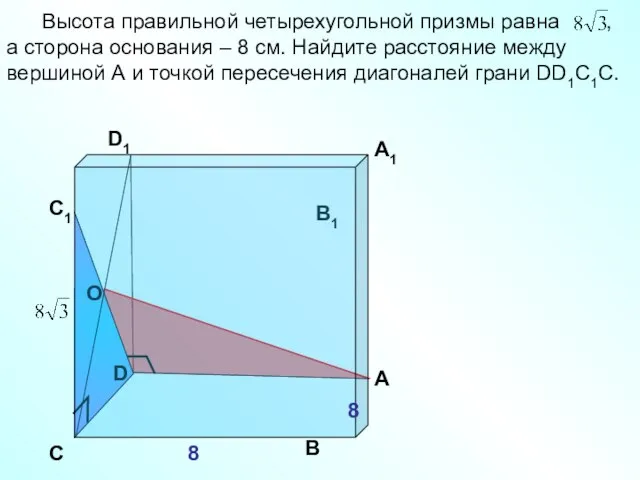
D
Высота правильной четырехугольной призмы равна , а сторона основания – 8 см. Найдите расстояние между вершиной А и точкой пересечения диагоналей грани DD1С1С.
С1
В1
А1
D1
С
В
А
О
8
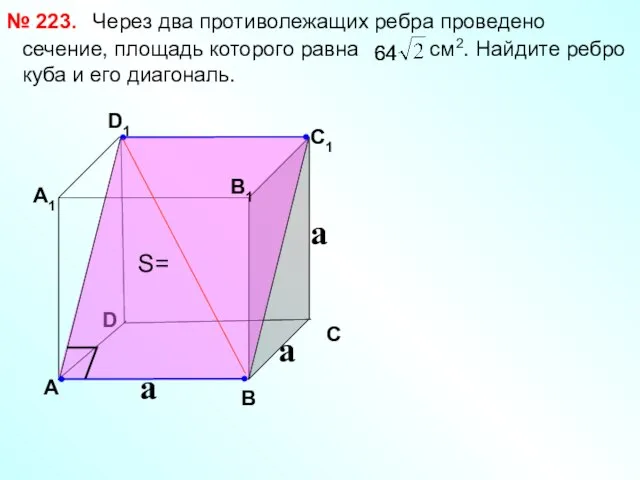
8

Через два противолежащих ребра проведено
сечение, площадь которого равна см2. Найдите ребро куба и его диагональ.
№ 223.
D
А
В
С
А1
D1
С1
В1
a
a
a
S=

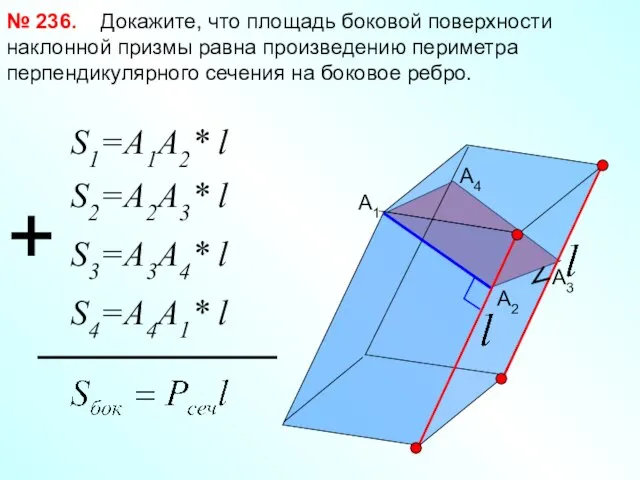
Докажите, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
№ 236.
A3
A4
S1=A1A2* l
S2=A2A3* l
S3=A3A4* l
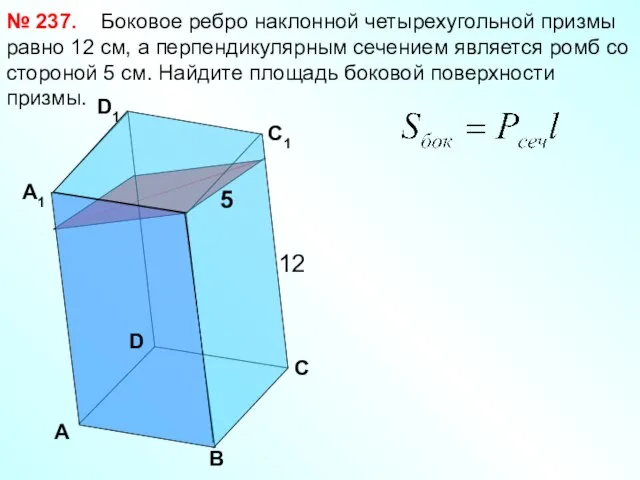
S4=A4A1* l

Боковое ребро наклонной четырехугольной призмы равно 12 см, а перпендикулярным сечением является ромб со стороной 5 см. Найдите площадь боковой поверхности призмы.
№ 237.
А
В
С
D
А1
D1
С1
12
5

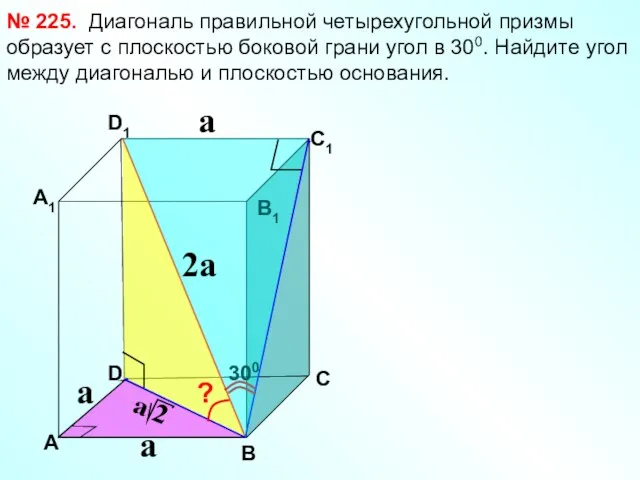
Диагональ правильной четырехугольной призмы образует с плоскостью боковой грани угол в 300. Найдите угол между диагональю и плоскостью основания.
№ 225.
В
С
А1
D1
С1
В1
D
А
a
2a

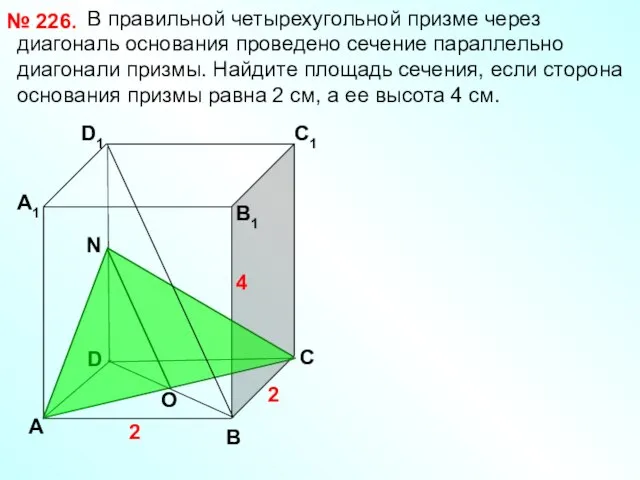
В правильной четырехугольной призме через диагональ основания проведено сечение параллельно диагонали призмы. Найдите площадь сечения, если сторона основания призмы равна 2 см, а ее высота 4 см.
№ 226.
D
А
В
С
D1
С1
В1
А1
2
2
4
O
N

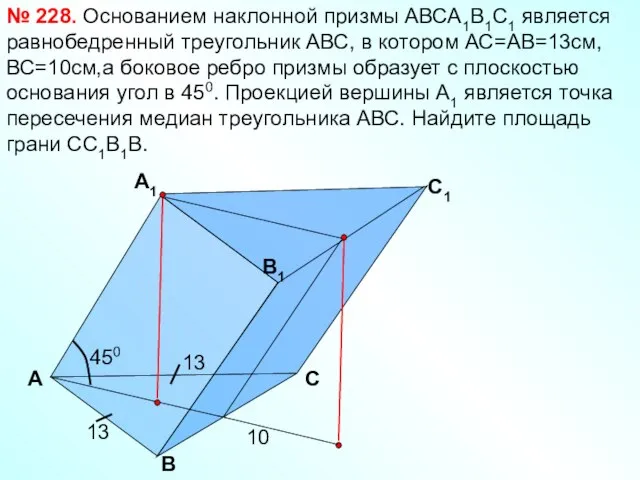
А
B
C1
B1
А1
C
Основанием наклонной призмы АВСА1В1С1 является равнобедренный треугольник АВС, в котором АС=АВ=13см, ВС=10см,а боковое ребро призмы образует с плоскостью основания угол в 450. Проекцией вершины А1 является точка пересечения медиан треугольника АВС. Найдите площадь грани СС1В1В.
№ 228.
13
13
10

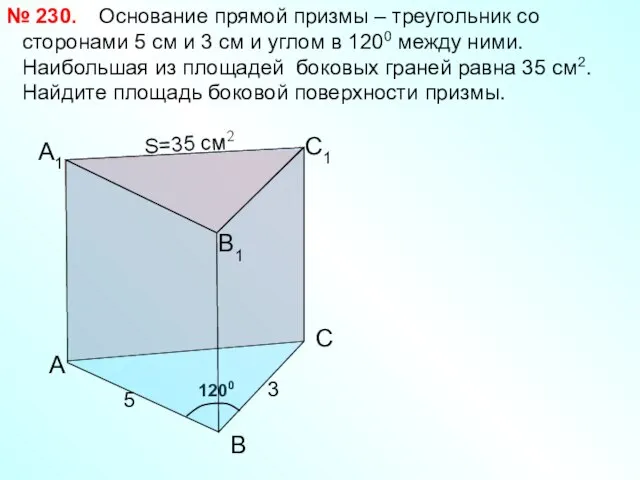
1200
А1
Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом в 1200 между ними. Наибольшая из площадей боковых граней равна 35 см2. Найдите площадь боковой поверхности призмы.
№ 230.
А
В
С
С1
В1
3
5
S=35 см2

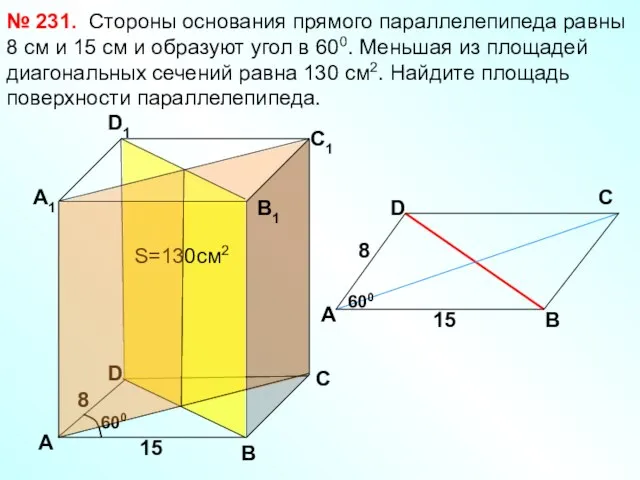
Стороны основания прямого параллелепипеда равны 8 см и 15 см и образуют угол в 600. Меньшая из площадей диагональных сечений равна 130 см2. Найдите площадь поверхности параллелепипеда.
№ 231.
В
С
А1
D1
С1
В1
D
8
15
600
S=130см2
А

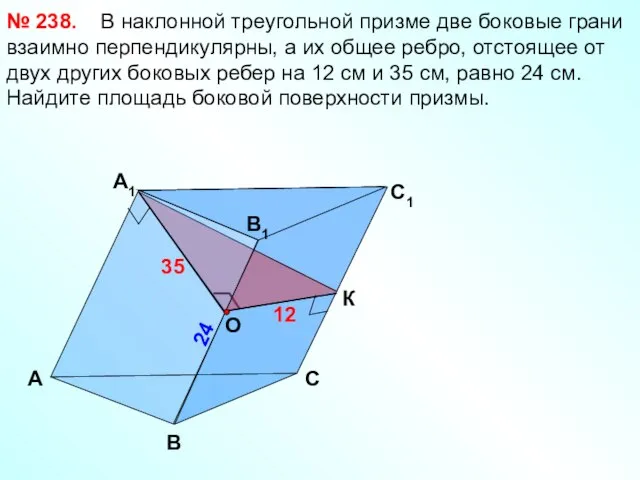
А
B
24
C1
B1
А1
C
35
12
В наклонной треугольной призме две боковые грани взаимно перпендикулярны, а их общее ребро, отстоящее от двух других боковых ребер на 12 см и 35 см, равно 24 см. Найдите площадь боковой поверхности призмы.
№ 238.

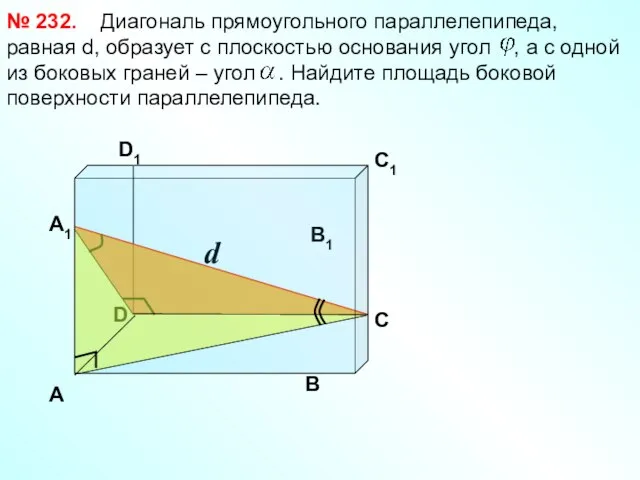
D
d
Диагональ прямоугольного параллелепипеда, равная d, образует с плоскостью основания угол , а с одной из боковых граней – угол . Найдите площадь боковой поверхности параллелепипеда.
№ 232.
А1
В1
С1
D1
А
В
С

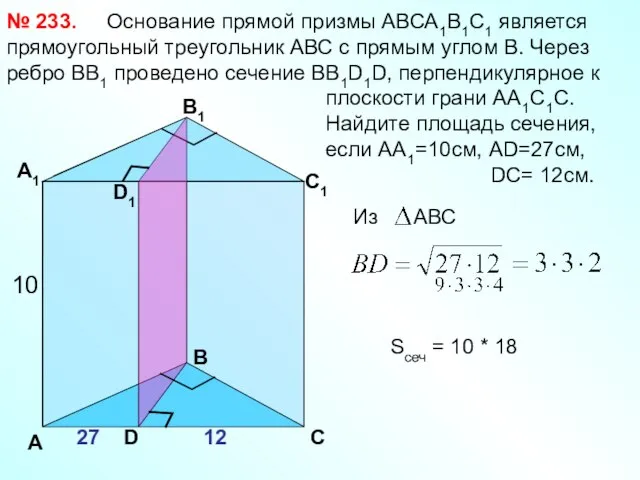
Основание прямой призмы АВСА1В1С1 является прямоугольный треугольник АВС с прямым углом В. Через ребро ВВ1 проведено сечение ВВ1D1D, перпендикулярное к
плоскости грани АА1С1С.
Найдите площадь сечения,
если АА1=10см, АD=27см,
DC= 12см.
№ 233.
А
С
В
В1
А1
С1
10
27
12
Sсеч = 10 * 18

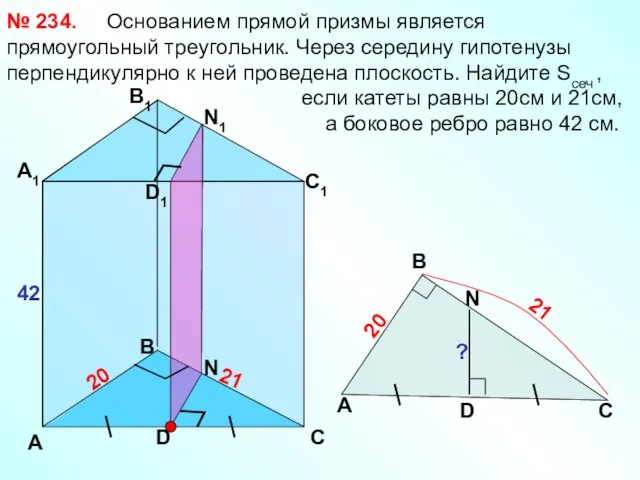
Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузы перпендикулярно к ней проведена плоскость. Найдите Sсеч ,
если катеты равны 20см и 21см,
а боковое ребро равно 42 см.
№ 234.
А
С
В
В1
А1
С1
42
20
21

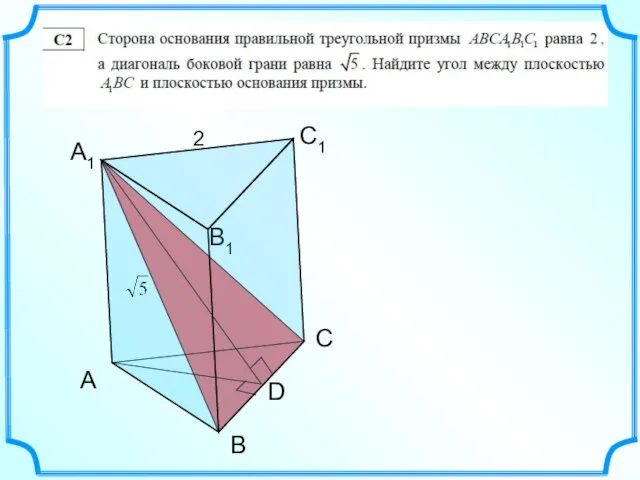
А
В
С
С1
В1
А1
2
D