Проект на тему: « Подобие треугольников»

Из истории о подобии
Отношение и Пропорциональность отрезков.
Идея отношения и Пропорции зародилась в глубокой древности. Об этом свидетельствуют древнеегипетские храмы, детали гробницы Менеса и знаменитых пирамид в Гизе (III тысячелетие до н. э.), вавилонские зиккураты (ступенчатые культовые башни), персидские Дворцы, Индийские и другие Памятники древности, Многие обстоятельства. В том числе особенности архитектуры, требования Удобства, Эстетики, техники и экономичности при возведении зданий и сооружений, вызвали возникновение и развитие понятий отношения и пропорциональности отрезков, площадей и других величин.

В «Московском» папирусе при рассмотрении, отношения большего катета к меньшему в одной из задач на прямоугольный треугольник применяется специальный знак для понятия «отношение».
В «Началах» Евклида учение об отношениях излагается дважды, В VII книге содержится арифметическая теория. Она относится только к соизмеримым величинам и к целым числам. Эта теория создана на основе практики действия с дробями. Евклид применяет ее для исследования свойств целых чисел. В V книге излагается общая теория отношений и пропорций, разработанная Евдоксом. Она лежит в основе учения о подобии фигур, изложенного в VI книге «Начал».

О подобии
Одинаковые по форме, но различные по величине фигуры встречаются в вавилонских и египетских памятниках. В сохранившейся погребальной камере отца фараона Рамсеса II имеется стена, покрытая сетью квадратиков, с помощью которой на стену перенесены в увеличенном виде рисунки меньших размеров.
Пропорциональность отрезков, образующихся на прямых, пересеченных несколькими параллельными прямыми, была известна еще вавилонским ученым, хотя некоторые приписывают это открытие Фалесу Милетскому. До наших дней сохранилась клинописная табличка, в которой речь идет о построении пропорциональных отрезков путем проведения в прямоугольном треугольнике параллелей к одному из катетов.

Учение о подобии фигур на основе теории отношений и пропорции было создано в Древней Греции в V—IV вв. до н. э. трудами Гиппократа Хиосского, Ар хита Тарентского, Евдокса Книдского и др. Оно изложено в VI книге «Начал» Евклида, начинающиеся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны».

Признаки подобия треугольника
Определение:
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Первый признак
По острому углу
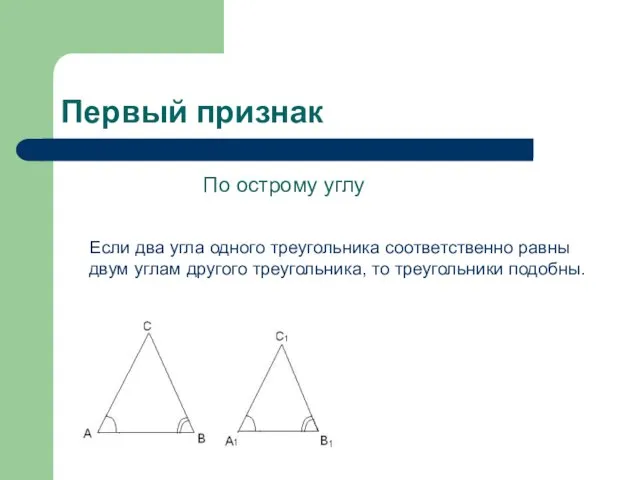
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.

Второй признак
По двум катетам
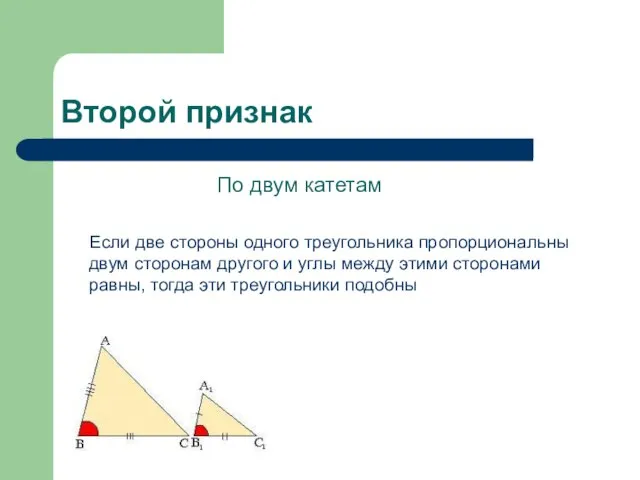
Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, тогда эти треугольники подобны

Третий признак
По катету и гипотенузе
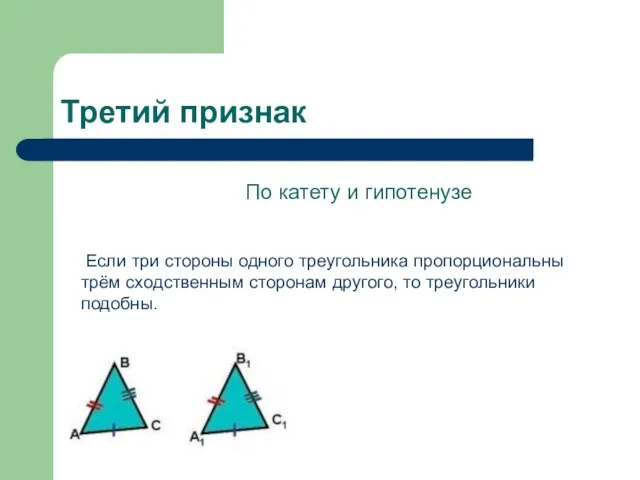
Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.

Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.

Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника

Средняя линия треугольника
Свойства
средняя линия треугольника параллельна третьей стороне и равна её половине.
при проведении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти площади исходного треугольника.

Вопросы на “засыпку”.
В повседневной жизни нам часто приходится сталкиваться с различными проявлениями подобия, однако подобие в обыденном смысле и с математической точки зрения – не одно и то же. Поэтому ответьте на вопрос:
будут ли подобными две банки емкостью 3 л и 1 л?
Будут ли подобны два четырехугольника, у которых соответственно равны все углы?

Задача 1
При постройке кровель, мостов, подъемных кранов скрепляют опорные брусья или балки так чтобы они образовали систему треугольников. Почему такое расположение балок лучше обеспечивает жесткость формы сооружения, нежели иное?

Из третьего признака равенства треугольников следует, что треугольник - жёсткая фигура. Поясним, что это означает. Представим себе две рейки, у которых два конца скреплены гвоздем (рис.1). Такая конструкция не является жёсткой: сдвигая или раздвигая свободные концы реек, мы можем менять угол между ними. Теперь возьмем ещё одну рейку и скрепим её концы со свободными концами первых двух реек (рис. 2). Полученная конструкция - треугольник - будет уже жёсткой. В ней нельзя сдвинуть или раздвинуть никакие две стороны, т. е. нельзя изменить ни один угол. Действительно, если бы это удалось, то мы получили бы новый треугольник, не равный исходному. Но это невозможно, так как новый треугольник должен быть равен исходному по третьему признаку равенства треугольников.
Именно поэтому лучшее расположение балок такое.

Задача 2.1
От пункта А, расположенного на берегу, к пункту В, лежащему на острове, требуется провести телефонную связь. Как не переплывая на остров, определить необходимое количество (длину) телефонного кабеля? Какой признак равенства треугольников здесь можно использовать? (Пункты А и В расположены на берегах, а кабель прокладывается по дну реки, т. е. условно ищем длину отрезка АВ)

Провесив прямую АС, отложим АС = СА1. < САВ измерим астролябией (или теодолитом) и через точку А1 провесим прямую А1В1 так, чтобы < СА1В1 = < САВ. Тогда треугольник АВС равен треугольнику А1В1С (по стороне и двум прилежащим углам). Искомая длина кабеля А1В1.

Задача 2.2
Найти длину острова АВ, не переплывая на остров.

На берегу выберем точку С, из которой видны точки А и В (рис. 4), провесим прямые АС и ВС. Отложим СА1 = СА, СВ1 = СВ. Расстояние А1В1 будет равно искомому расстоянию АВ, т. к. треугольник АВС равен треугольнику А1В1С по двум сторонам и углу между ними (СА1 = СА, СВ1 = СВ, угол ВСА равен углу А1СВ1, как вертикальные)

Ресурсы
http://ru.wikipedia.org/wiki/Подобие_треугольников
http://rudocs.exdat.com/docs/index-12452.html
http://ru.wikipedia.org/wiki/%D1%F0%E5%E4%ED%FF%FF_%EB%E8%ED%E8%FF
http://www.ankolpakov.ru/wp-content/uploads/2010/09/2-признак-подобия-треугольников1.jpg
http://900igr.net/datai/geometrija/Urok-Priznaki-podobija-treugolnikov/0001-002-Urok-geometrii-Priznaki-podobija-treugolnikov.png
http://900igr.net/datai/geometrija/Podobnye-treugolniki/0005-001-Opredelenie-podobnykh-treugolnikov.jpg
http://900igr.net/datai/geometrija/Podobie-treugolnikov-8-klass/0002-002-1-priznak-podobija-treugolnika.png
http://900igr.net/datai/geometrija/Zadachi-na-podobie/0002-003-Temy-zadach.png
http://www2.springfield.k12.il.us/schools/enos/blurbs/7_1259529541.jpg
http://59209s006.edusite.ru/images/logo2.gif
http://oldskola1.narod.ru/Nikitin/280.gif
http://img-fotki.yandex.ru/get/54/art-alex3036.13/0_143e7_284f5009_XL
http://upload.wikimedia.org/wikipedia/commons/2/22/Tour_Eiffel_1878.jpg
http://www.lika-clipart.ru/school/sc002.gif
http://mathdaily.files.wordpress.com/2010/06/math1.gif
http://images03.olx-st.com/ui/2/50/96/35114496_2.jpg
http://static.vmurmanske.ru/serverdata/news_info/2010/04/26/572783/imgFull.jpg
http://www.sp7siedlce.home.pl/images/mat.jpg
http://school.discoveryeducation.com/clipart/images/divider.gif
http://www.proshkolu.ru/content/media/pic/std/1000000/952000/951258-437ddd78aa8e0a21.gif