Содержание
- 2. Простая биномиальная модель оценки премии опциона значение опциона и курса акций рассматривается только в начале и
- 3. Простая биномиальная модель оценки премии европейского опциона call Т0: t – количество месяцев; Passet(T0) – цена
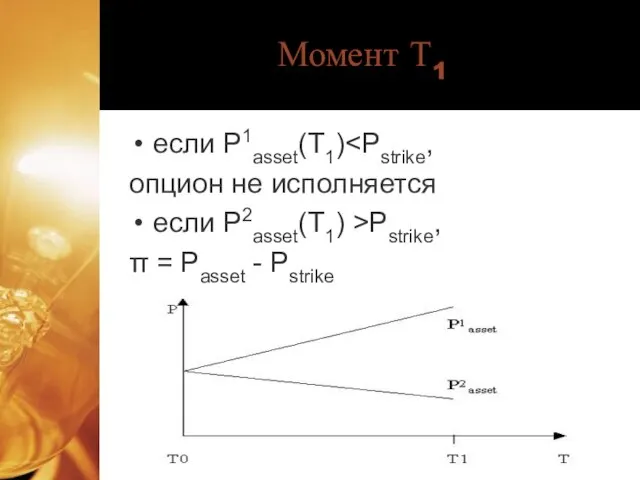
- 4. Момент Т1 если P1asset(T1) опцион не исполняется если P2asset(T1) >Pstrikе, π = Passet - Pstrike
- 5. Портфель без риска Портфель: покупка n акций и продажа 1опциона Портфель без риска, Vportfolio: n*P1asset(T1) =
- 6. Стоимость портфеля Т0: Passet(T0)*n – π= Vportfolio*e-i*t/12 π = Passet(T0)*n – Vportfolio*e-i*t/12
- 7. Числовой пример европейский опцион call t=5 мес Passet(T0)=$33; Pstrike=$36; i=10%; P1asset(T1) = 34; P2asset(T1) = 38
- 9. Скачать презентацию





 Алгоритмическое моделирование
Алгоритмическое моделирование Военная техника Великой Отечественной войны
Военная техника Великой Отечественной войны Дети войны
Дети войны Оценочные процедуры в РСОКО. Анализ опыта Чувашской Республики.
Оценочные процедуры в РСОКО. Анализ опыта Чувашской Республики. Самостоятельная работа № 3-4 от 06
Самостоятельная работа № 3-4 от 06 швы
швы Проект «Курить – жизнь загубить!»
Проект «Курить – жизнь загубить!» Воспитательный аспект образовательного процесса
Воспитательный аспект образовательного процесса Презентация на тему Металлы и неметаллы
Презентация на тему Металлы и неметаллы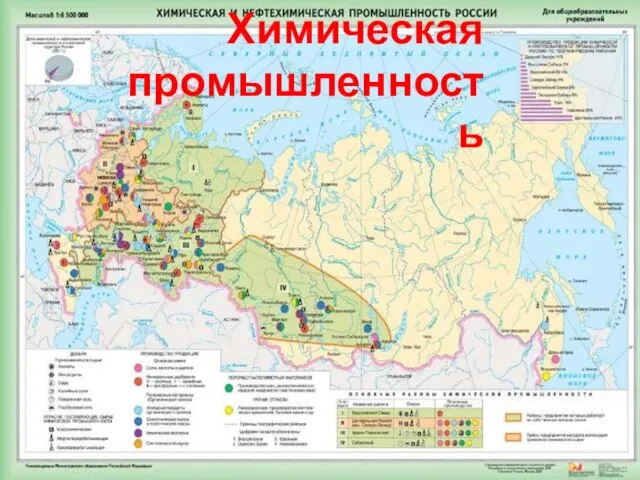 Презентация на тему Химическая промышленность
Презентация на тему Химическая промышленность  Презентация на тему Кто работает ночью 1 класс
Презентация на тему Кто работает ночью 1 класс учитель английского языка МОУ Прогимназия №1 Шашкова Лилия Владимировна г. Электрогорск Ул. Советская д. 5 кв. 72. Тел. 3-47-49 2008 год
учитель английского языка МОУ Прогимназия №1 Шашкова Лилия Владимировна г. Электрогорск Ул. Советская д. 5 кв. 72. Тел. 3-47-49 2008 год ИНФОРМАЦИОННАЯ СТРАТЕГИЯ ПО ВИЧ/СПИДу В РЕСПУБЛИКЕ БЕЛАРУСЬ
ИНФОРМАЦИОННАЯ СТРАТЕГИЯ ПО ВИЧ/СПИДу В РЕСПУБЛИКЕ БЕЛАРУСЬ Многообразие насекомых, их роль в природе и жизни человека
Многообразие насекомых, их роль в природе и жизни человека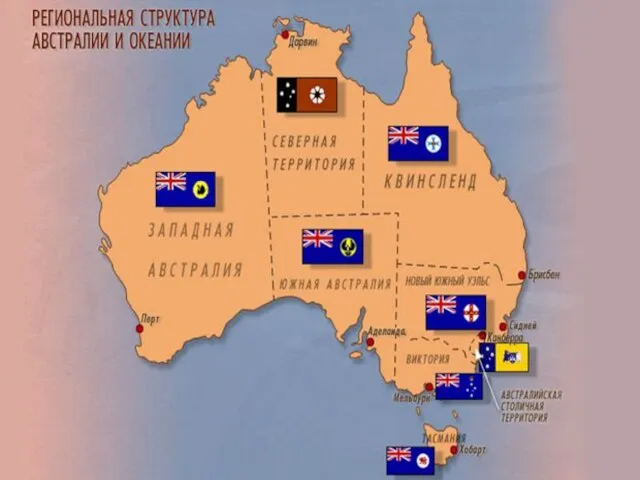 Австралия и Океания.
Австралия и Океания. Виды предложений по цели высказывания и по интонации
Виды предложений по цели высказывания и по интонации Моторные расстройства при паркинсонизме и их влияние на качество жизни пациента
Моторные расстройства при паркинсонизме и их влияние на качество жизни пациента Нектар воспевания святого имени – Намамрита
Нектар воспевания святого имени – Намамрита Зачетная работа. Организационная структура отеля Крокус
Зачетная работа. Организационная структура отеля Крокус Учение Платона о государстве и праве
Учение Платона о государстве и праве Политическая сфера общества
Политическая сфера общества Времена года. Зимний лес
Времена года. Зимний лес «Снимать можно чем угодно,
«Снимать можно чем угодно, Swot-анализ
Swot-анализ К 50- летию космонавтики. Звёздное небо -это небольшая часть безграничного космоса. Земляне всех поколений всегда смотрели на него с
К 50- летию космонавтики. Звёздное небо -это небольшая часть безграничного космоса. Земляне всех поколений всегда смотрели на него с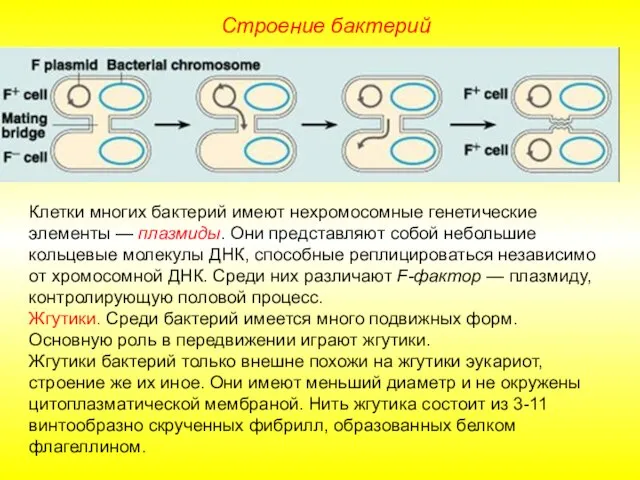 Строение бактерий
Строение бактерий Государство. понятие, признаки, сущность, социальное назначение, функции
Государство. понятие, признаки, сущность, социальное назначение, функции Шапки
Шапки