Прямая и обратная пропорциональная зависимость

Две величины называют прямо пропорциональными, если при увеличении(уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Две величины называют обратно пропорциональными, если при увеличении(уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.

Задача 1. Один велосипедист проехал расстояние 24 км со скоростью 12 км/ч. Какое расстояние проедет за это время другой велосипедист, скорость которого 10,5 км/ч?
Решение: Пусть второй велосипедист за это же время пройдет x км.
Скорость Расстояние
1 велосипедист 12 км/ч 24 км
2 велосипедист 10,5 км/ч x км
Т.к. скорость и расстояние прямо пропорциональные величины, составим пропорцию: 12:10,5=24:x
Ответ: 21 км

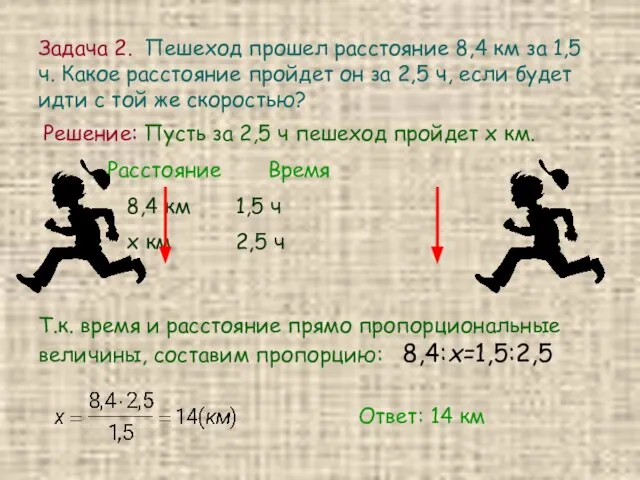
Задача 2. Пешеход прошел расстояние 8,4 км за 1,5 ч. Какое расстояние пройдет он за 2,5 ч, если будет идти с той же скоростью?
Решение: Пусть за 2,5 ч пешеход пройдет x км.
Расстояние Время
8,4 км 1,5 ч
x км 2,5 ч
Т.к. время и расстояние прямо пропорциональные величины, составим пропорцию: 8,4:x=1,5:2,5
Ответ: 14 км

Задача3. Теплоход на подводных крыльях прошел расстояние между пристанями со средней скоростью 60 км/ч за 2,5 ч. За сколько времени пройдет это расстояние теплоход, если будет идти со скоростью 50 км/ч?
Решение: Пусть с новой скоростью теплоход пройдет
расстояние за x ч. Скорость Время
60 км/ч 2,5 ч
50 км/ч x ч
Т.к. скорость и время обратно пропорциональны, составим пропорцию:60:50 = x:2,5
Ответ: 3 часа

Задача 4. Теплоход «Ракета» прошел расстояние между пристанями со скоростью 50 км/ч за 4,8 ч. С какой скоростью должен идти теплоход, чтобы пройти это расстояние за 3,2 ч.
Решение: Пусть новая скорость теплохода расстояние x км/ч. Скорость Время
50 км/ч 4,8 ч
x км/ч 3,2 ч
Т.к. скорость и время обратно пропорциональны, составим пропорцию: 50:x = 3,2:4,8
Ответ: 75 км/ч