Работа с одномерными и двумерными массивами

Массив
последовательность логически связанных элементов одного типа, которым присвоено одно имя.
Размерность массива – это количество индексов у каждого элемента массива.
TYPE <имя типа> = ARRAY [индекс] OF <тип эл-тов >;
Buffer1: ARRAY [1..10] of Integer;
Buffer2: ARRAY [1..10, 1..10] of Integer;

Массивы могут быть
Одномерные (вектор)
Многомерные (матрицы)
Открытые

Размер массива
C:array [1..5] of char;;
Addr(C[i]) = Addr(C) + i*sizeof(char);
D:array [Rows,Cols] of integer;;
Addr(D[j,i]) = Addr(D) + (j*Cols+i)*sizeof(int);
где (j*Cols+i) – порядковый номер элемента в памяти при обходе массива.

Массив можно создать несколькими способами:
const n = 20;
m=10;
type
months = (jan, feb, mar, apr, may, jun, jul, aug, sep, oct, nov, dec);
years = 1900..2100;
people = array[years] of longint;
arr = array[1..4, 1..3] of integer;
сonst cords: arr = ((1,-1,3), (0,0,0), (1,4,0), (4,-1,-1));
var
growth: array[months] of real;
hum: people;
notes: array[1..n] of string;
Narod:array [1..m] people;
matrix = array [1..n, 1..m] of integer;

Инициализация массива
Если значения элементов массива определены до начала работы программы
Если исходные данные необходимо внести с клавиатуры в процессе выполнения программы
Прямое присвоение в теле программы значений элементам массива

Инициализация массива
CONST
A: ARRAY [1..10] OF REAL =
(0.1, -15.3, 7, 0, -11.89, 4, -78,11.2, 1,0.01);
{ A[1]=0.1, A[2]=-15.3 … A[10]=0.01}
M: ARRAY [1..5, 1..2] OF REAL =
((0.1, -15.3), (7, 0), (-11.89,4), (-78,11.2), (1,0.01));
{M[1,1] = 0.1, M[1,2] = -15.3,
M[2, 1] = 7, M[2, 2] = 0,
...
M[5,1]=1, M[5, 2]= - 0.01}

Инициализация массива
CONST
M = 3;
N = 4;
VAR
A: ARRAY[ 1.. М, 1.. N] OF REAL;
begin
…
FOR I := 1 ТО М DO
FOR J:= 1 TO N DO
READ(A[I,J]);
…
end.

Инициализация массива
FillChar( var V; Count: Word; B: Byte );
Для обнуления массива A[1..10] of Real можно записать:
FillChar(A, 40, 0); или FillChar(A, SizeOf(A), 0);
FOR I := 1 ТО М DO
FOR J:=l TO N
DO A[I,J]:=0;

Обращение к элементам массива
var
ch: array [1..11] of char;
i: integer;
begin
for i := 1 to 11 do
read (ch[i]);
for i := 1 to 11 do write (ch[i]:3);
readln
end.
const n=3; m=5;
var matrix: array[1..3,1..5] of integer;
i, j: integer;
begin
writeln ('Введите 15 чисел: ');
for i := 1 to n do
for j := 1 to m do
read (matrix[i,j]);
for i := 1 to n do
begin
for j := 1 to m do
write (matrix[i][j]:5);
writeln ;
end;
readln
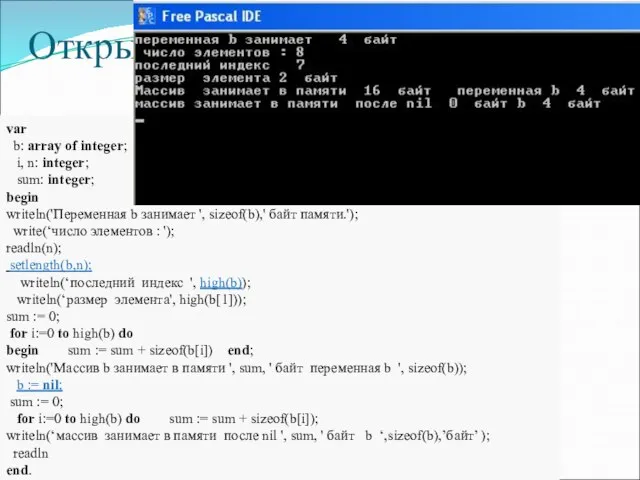
end.

Открытый массив
< имя_массива>: array of <тип эл-тов>;
mas2: array of integer;
var
b: array of integer;
i, n: integer;
sum: integer;
begin
writeln('Переменная b занимает ', sizeof(b),' байт памяти.');
write(‘число элементов : ');
readln(n);
setlength(b,n);
writeln(‘последний индекс ', high(b));
writeln(‘размер элемента', high(b[1]));
sum := 0;
for i:=0 to high(b) do
begin sum := sum + sizeof(b[i]) end;
writeln('Массив b занимает в памяти ', sum, ' байт переменная b ', sizeof(b));
b := nil;
sum := 0;
for i:=0 to high(b) do sum := sum + sizeof(b[i]);
writeln(‘массив занимает в памяти после nil ', sum, ' байт b ‘,sizeof(b),’байт’ );
readln
end.

Вычисление индекса массива
Пример программы с ошибкой массива Паскаля
Program primer _ error ;
Type
vector=array [1..80] of word;
var
n: integer;
a: vector;
begin
n:=45;
a[n*2]:=25;
end .

Заполнение матрицы «по спирали»
var
a:array[1..100,1..100]of integer;
i,imax,imin,
j,jmax,jmin,k,m,n:integer;
begin
write('Vvedite 4islo strok: '); readln(m);
write('Vvedite 4islo stolbcov: ');
readln(n);
jmin:=1;
jmax:=n;
imin:=2;
imax:=m;
k:=0;

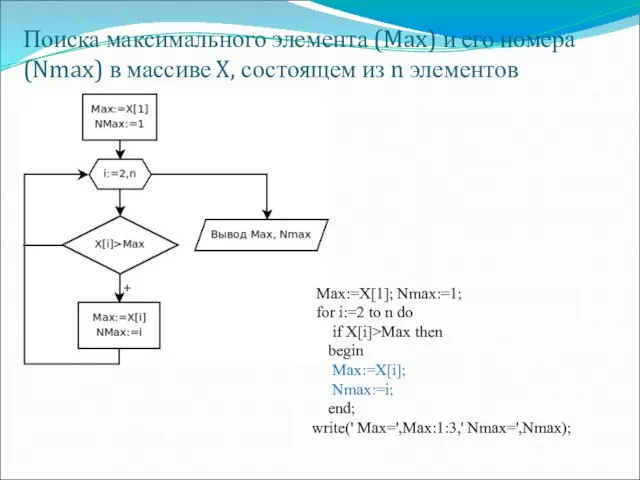
Поиска максимального элемента (Max) и его номера (Nmax) в массиве X, состоящем из n элементов
Max:=X[1]; Nmax:=1;
for i:=2 to n do
if X[i]>Max then
begin
Max:=X[i];
Nmax:=i;
end;
write(' Max=',Max:1:3,' Nmax=',Nmax);

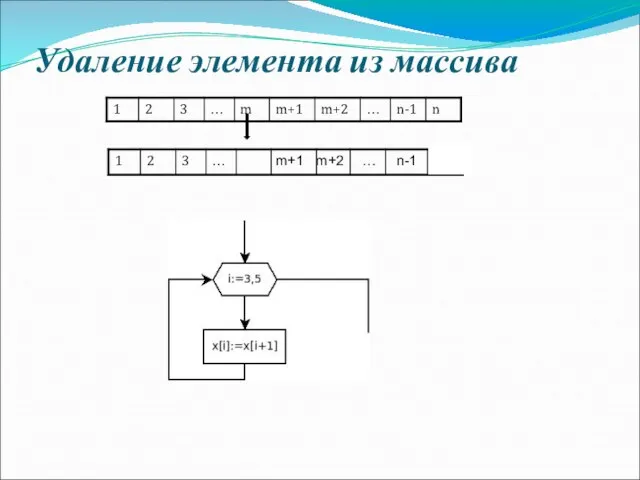
Удаление элемента из массива
m+1
m+2
…
n-1
n

Пример: Удалить из массива X(n) отрицательные элементы.
while(i<=n)do
if x[i]<0 then
begin
for j:=i to n-1 do
x[j]:=x[j+1];
n:=n-1;
end
Else
i:=i+1;
writeln('Измененный массив:');
for i:=1 to n do
write (X[i]:5:2,' ');
writeln;
end.

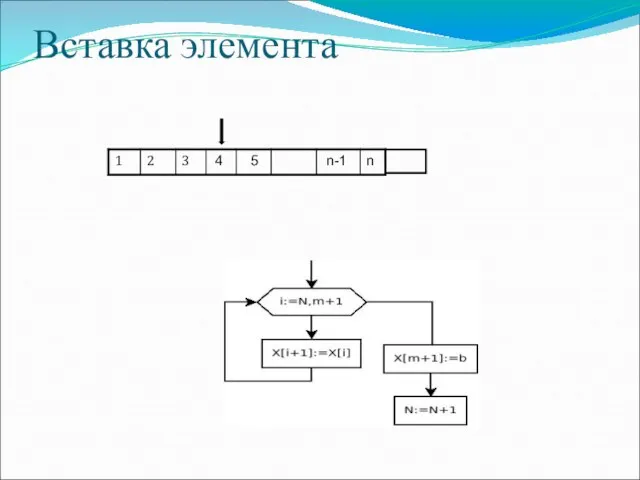
Вставка элемента
4
5
n-1
n

Вставка элемента
var i,n,m:byte; X: array [1..100] of real;
b:real;
begin
write ('N='); readln (n);
for i:=1 to n do
begin
write('X[', i ,']='); readln (X[i]);
end;
writeln ('m='); readln (m);
writeln ('b='); readln(b);
for i:=n downto m+1 do
x[i+1]:=x[i];
x[m+1]:=b;
n:=n+1;
writeln('Измененный массив');
for i:=1 to n do write (X[i]:5:2,' ');
writeln;
end.

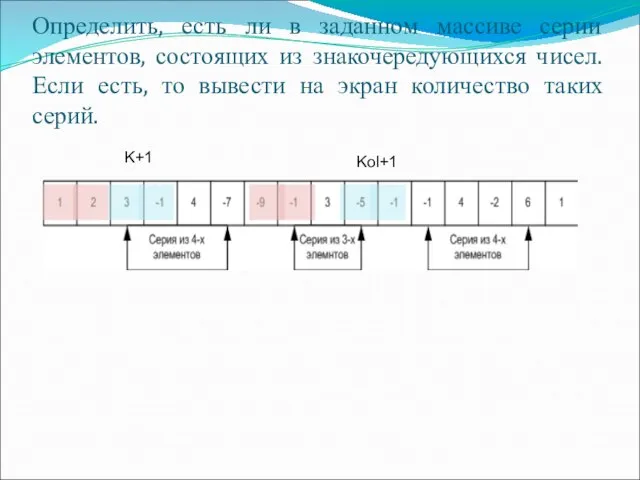
Определить, есть ли в заданном массиве серии элементов, состоящих из знакочередующихся чисел. Если есть, то вывести на экран количество таких серий.
K+1
Kol+1

{
var
x:array[1..50] of real;
n,i,k,kol:integer;
begin
write('n=');
readln(n);
for i:=1 to n do
read(x[i]);
k:=1;
kol:=0;
for i:=1 to n-1 do
if x[i]*x[i+1]<0 then
k:=k+1
else
begin
if k>1 then
kol:=kol+1;
k:=1;
end;
If k>1 then
kol:=kol+1;
If kol>0 then
write('Количество знакочередующихся серий=',kol)
else
write('Знакочередующихся серий нет')
end.

Определить является ли данный массив возрастающим
PROGRAM z_array;
USES crt;
Var A: array[1..100] of real;
N,i:byte;
Flag: boolean;
begin
clrscr;
writeln(' Количество элементов массива');
readln(N);
for I := 1 to N do
begin
write('[', I ,']= ');
readln(A[I]);
end;
Flag := false;
for I := 1 to N - 1 do
if A[I] >=A[I + 1] then
begin Flag := true;
break;
end;
if Flag = false then
writeln('Массив является
возрастающим')
else
writeln('Массив не является возрастающим ');
readln;
end.

Свойства элементов матрицы
если номер строки элемента совпадает с номером столбца (i=j) - элемент лежит на главной диагонали матрицы;
если номер строки превышает номер столбца (i>j), то элемент находится ниже главной диагонали;
если номер столбца больше номера строки (i
элемент лежит на побочной диагонали, если его индексы удовлетворяют равенству i+j–1=n;
неравенство i+j–1
соответственно, элементу, лежащему ниже побочной диагонали, соответствует выражение i+j–1>n.

Найти сумму элементов матрицы, лежащих выше
главной диагонали
var
a:array [1..15,1..10] of real;
i,j,n,m: integer;
s: real;
Begin write(' количество строк: ');
readln (n);
write('количество столбцов: ');
readln (m);
writeln('Матрица A:');
for i:=1 to n do
for j:=1 to m do
Read(a[i,j]);
s:=0;
for i:=1 to n do
for j:=i+1 to m do
s:=s+a[i,j];{ накапливаем сумму. }
writeln('сумма элементов матрицы', s:8:3);
end.

Найти седловой элемент(ы) и его координаты, либо сообщить, что таковой нет
Program z_array;
uses crt;
var A: array [1..100,1..100] of real;
N, M, I, J, K, L:byte;
Flag1,Flag2:boolean;
begin
write(‘число строк ');
readln(N);
write(‘ число столбцов ');
readln(M);
L:=0;
for I := 1 to N do
for J := 1 to M do
begin
write('[', I,',', J,']= ');
readln(A[I, J]);
end;
if Flag1 and Flag2 then
begin
writeln('Седловой элемент Строка: ',I,' Столбец: ',J);
inc(L);
end;
end;
if L = 0 then
writeln('Седловых элементов нет');
readln;
end.
for I := 1 to N do
for J := 1 to M do
begin
Flag1:=true; Flag2:=true;
K:=1;
while (Flag1)and(K <= N)do
if A[K, J] > A[I, J] then Flag1:=false
else inc(K);
If Flag1 Then
while (Flag2)and(K <= M)do
if A[i, K] > A[I, J] then Flag2:=false
else inc(K);

Транспонирование матрицы

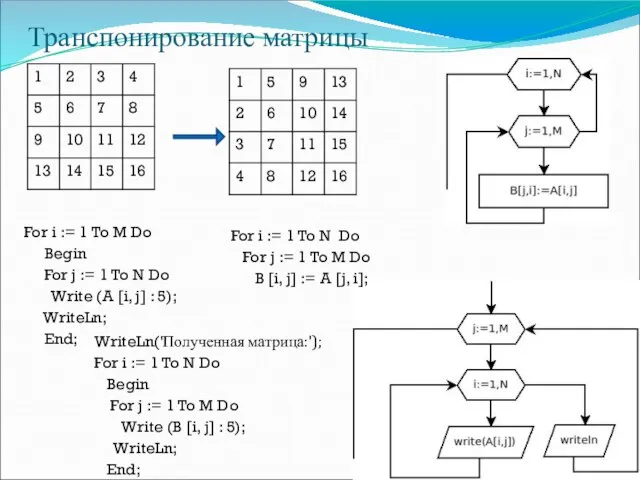
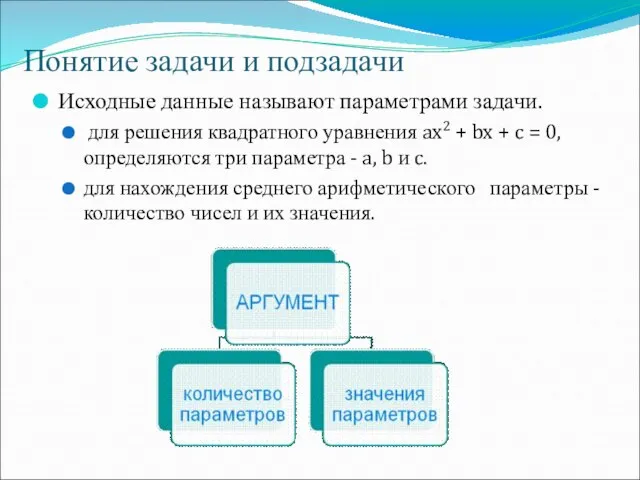
Понятие задачи и подзадачи
Исходные данные называют параметрами задачи.
для решения квадратного уравнения ax2 + bx + c = 0, определяются три параметра - a, b и c.
для нахождения среднего арифметического параметры - количество чисел и их значения.

Понятие задачи и подзадачи

Найти самую тяжелую монету из 10 монет.
"Самая тяжелая монета" из 1 монеты,
"Самая тяжелая монета" из 2 первых монет,
"Самая тяжелая монета" из 3 первых монет,
...
"Самая тяжелая монета" из 9 первых монет.
все они основываются на одной подзадаче: найти самую тяжелую из 2 монет.

Рекуррентное соотношение
соотношение, связывающее одни и те же функции, но с различными аргументами.
Правильное рекуррентное соотношение -соотношение, у которых количество или значения аргументов у функций в правой части меньше количества или значений аргументов функции в левой части соотношения. Если аргументов несколько, то достаточно уменьшения одного из аргументов.

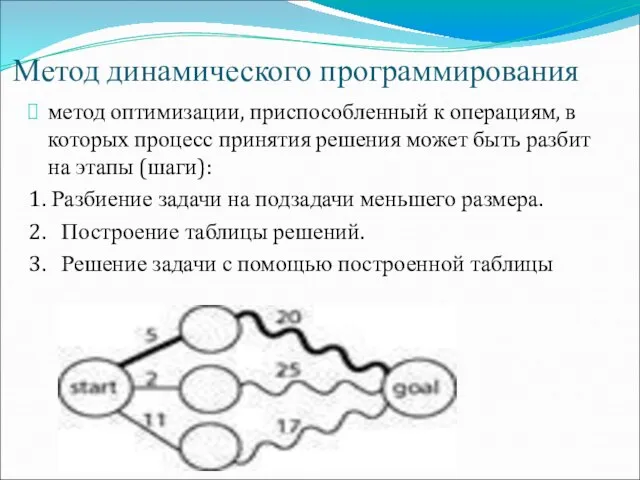
Метод динамического программирования
метод оптимизации, приспособленный к операциям, в которых процесс принятия решения может быть разбит на этапы (шаги):
1. Разбиение задачи на подзадачи меньшего размера.
2. Построение таблицы решений.
3. Решение задачи с помощью построенной таблицы

Динамическое программирование (ДП)
- метод решения задач путем составления последовательности из подзадач таким образом, что:
первый элемент последовательности (возможно несколько элементов) имеет тривиальное решение
последний элемент этой последовательности - это исходная задача
каждая задача этой последовательности может быть решена с использованием решения подзадач с меньшими номерами
Для T составляется {T1,T2,T3,…,Ti,…,Tn},
причем T=Tn и Ti=F(Ti-1)

Два подхода ДП
Нисходящее ДП - задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи.
Восходящее ДП - подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи.

Определить, сколькими различными способами можно подняться на 10-ю ступеньку лестницы, если за один шаг можно подниматься на следующую ступеньку или через одну.
Пусть K(10) -количество способов подъема на 10 ступеньку, K(i) количество способов подъема на i-ю ступеньку.
K(i) = K(i - 2) + K(i - 1), при i≥3
K(1) = 1, K(2) = 2.
K(i)
K[1] := 1;
K[2] := 2;
for i := 3 to 10 do
K[i] := K[i - 1] + K[i - 2];

В заданной числовой последовательности A[1..N] определить максимальную длину последовательности подряд идущих одинаковых элементов
L[1]: = 1;
For i:=2 to N do
if A[i-1]: = A[i] then
L[i]:=L[i-1]+1
else
L[i]:=1;
IndL:=1;
For i:=2 to N do
if L[i]>L[IndL] then
IndL:=i;
1
2
3
4
1

Для заданной числовой последовательности A[1.. N] найти максимальную длину строго возрастающей подпоследовательности элементов (не обязательно подряд идущих, но обязательно в порядке увеличения индексов) последовательности A.
2
3
4
4
5
L[1]: = 1;
For i:=2 to N do
If A[i]=A[i-1] then L[i]:=L[i-1]
Else
For j:=1 to i-1 do
if А[j]<А[i], then
L[i]:=L[j]+1;
IndL:=1;
For i:=2 to N do
if L[i] > L[IndL] then IndL:=i;
//результат L(ImdL)

Составить программу подсчета для натурального числа n количества всех его делителей.
Пусть dn(n) и dnx(n,x) - функции для решения исходной и обобщенной задач. dn(n)=dnx(n,n).
readln(n,x);
del[1]:=1
for I:=2 to x do
if n mod x=0 then
del[i]:=1+del[i-1]
else del[i]:=del[i-1];
end;
writeln(del[x]);
2
Пусть n=20
3
4
4

В таблице размера m*n, с элементами 0 и 1 найти квадратный блок максимального размера, состоящий из одних единиц.
Пусть T[i,j]- функция, значение которой равно размеру максимального квадратного блока из единиц, правый нижний угол которого расположен в позиции (i,j).
T[1,j] = a[1,j], T[i,1] = a[i,1].
T[i,j] =0, если A[i,j] = 0,
T[i,j] = min(T[i-1,j],T[i,j-1],T[i-1,j-1]) +1, при A[i,j] = 1.
1 1 0 1 0 1
1 1 1 1 1 0
1 0 1 1 1 1
1 1 1 1 1 1
1 0 1 1 0 1
1 1 0 1 0 1
1 2 1 1 1 0
1 0 1 2 2 1
1 1 1 2 3 2
1 0 1 2 0 1