РЕАЛЬНІ ГАЗИ

План
Відхилення реальних газів від законів для ідеальних газів.
Сили міжмолекулярної взаємодії.
Рівняння Ван-дер-Ваальса та його аналіз.
Порівняння ізотерм Ван-дер-Ваальса з експериментальними ізотермами. Інші рівняння стану реальних газів.

Література:
1. Кучерук І.М., Горбачук І.Т., Луцик П.П. Загаль-ний курс фізики: Навч. посібник. – Т.1.: Механіка. Молекулярна фізика і термодинаміка. – К.: Техні-ка, 1999. – 536 с. (с. 419 – 432).
2. Cергієнко В.П. Курс фізики: Навч. посібник. – К.: Майстер-клас, 2006. – 152 с. (с. 66 – 76).
3. Сергієнко В.П., Шут М.І. та ін. Демонстраційний експеримент з фізики: Навч. посібник. – К. “Просвіта”:, 2006. – 368 с.
4. Загальна фізика. Програма навчальної дисцип-ліни для студентів вищих педагогічних закладів освіти / М.І. Шут, І.Т. Горбачук, В.П. Сергієнко. – К.: НПУ, 2005. – 48 с.
5. www.npu.edu.ua/ebook/

Відхилення реальних газів від законів для ідеальних газів
Експериментально доведено, що закони ідеального газу виконуються при низьких тисках і порівняно високих температурах. В таблиці 9. 1 приведені результати експериментальної пере-вірки закону Бойля-Маріотта.
pV = const (9. 1)
Таблиця 9.1
Результати експериментальної перевірки закону Бойля-Маріотта
для певної маси азоту при T = 273 К

Чи можна не враховувати розмір молекул в реальному газі ?
Якщо створити тиск в 100 атм, то власний об’єм молекул складатиме від всього об’єму, в
1000 атм – . Отже, такий об’єм буде зайнятий для руху молекул, тому нехтувати розмірами молекул не можна.
в 1 м3 N = 2,7∙1025 (м3)-1 - число Лошмідта за нормальних умов. (1 атм, 0°C)

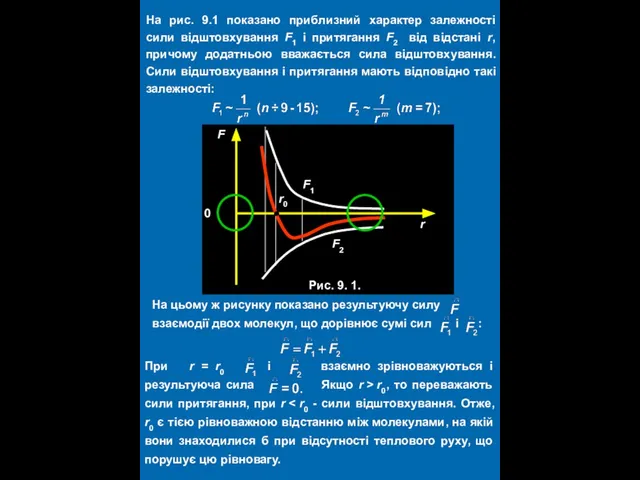
Сили міжмолекулярної взаємодії
При низьких температурах або при високих тисках, коли молекули знаходяться близько одна до одної, нехтувати не можна не тільки їхніми розмірами, а й силами взаємо-дії. Кожна молекула має скінченні розміри і є складною системою електричних заряджених частинок. Відбуваєть-ся їх електромагнітна взаємодія на відстані. Зокрема, здатність твердих тіл чинити опір розтягуванню приво-дить до висновку, що між молекулами речовини в будь-якому агрегатному стані діють сили взаємного притя-гання.

На цьому ж рисунку показано результуючу силу взаємодії двох молекул, що дорівнює сумі сил і :
На рис. 9.1 показано приблизний характер залежності сили відштовхування F1 і притягання F2 від відстані r, причому додатньою вважається сила відштовхування. Сили відштовхування і притягання мають відповідно такі залежності:
При r = r0 і взаємно зрівноважуються і результуюча сила Якщо r > r0, то переважають сили притягання, при r < r0 - сили відштовхування. Отже, r0 є тією рівноважною відстанню між молекулами, на якій вони знаходилися б при відсутності теплового руху, що порушує цю рівновагу.

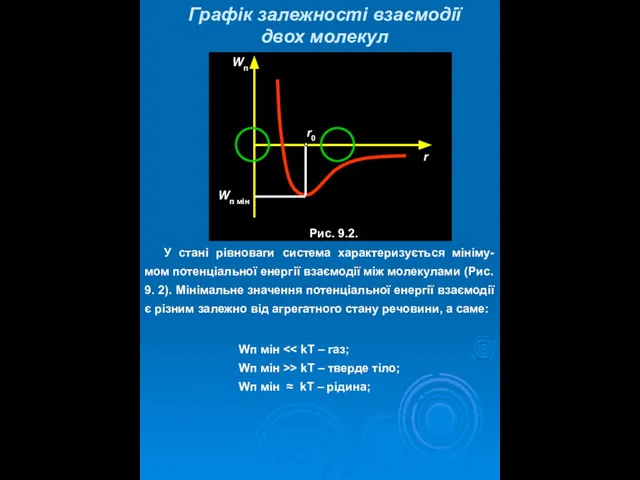
Графік залежності взаємодії двох молекул
У стані рівноваги система характеризується мініму-мом потенціальної енергії взаємодії між молекулами (Рис. 9. 2). Мінімальне значення потенціальної енергії взаємодії є різним залежно від агрегатного стану речовини, а саме:
Wп мін << kT – газ;
Wп мін >> kT – тверде тіло;
Wп мін ≈ kT – рідина;
r
r0
Wп
Wп мін
Рис. 9.2.

Рівняння Ван-дер-Ваальса
та його аналіз
Вперше врахував вплив молекулярних сил і, користуючись моделлю молекул, як твердих пружних куль (рис. 9. 3), вніс поправки до рівняння стану ідеального газу в 1873 р. у праці «Про неперервність газоподібного і рідкого станів» нідерландський фізик Ван-дер-Ваальс (1837 – 1923).

Рівняння Ван-дер-Ваальса та його аналіз.
Знайдемо значення об’єму b. Уявимо собі посудину в формі куба, об’ємом VМ, який займає 1 моль газу за даних тиску і температури. (рис.9.4)
Сторона куба дорівнює . Нехай діаметр молекули дорівнює d, а радіус r = . Припустимо, що спочатку в нашій посудині міститься всього одна молекула. Для її руху (точніше для руху її центра) доступним є увесь об’єм посудини, за вирахунком шару товщиною r, що прилягає до стінки. Наша молекула може рухатися в об’ємі куба зі стороною на d менше ніж сторона посуди-ни. Цей об’єм дорівнює:

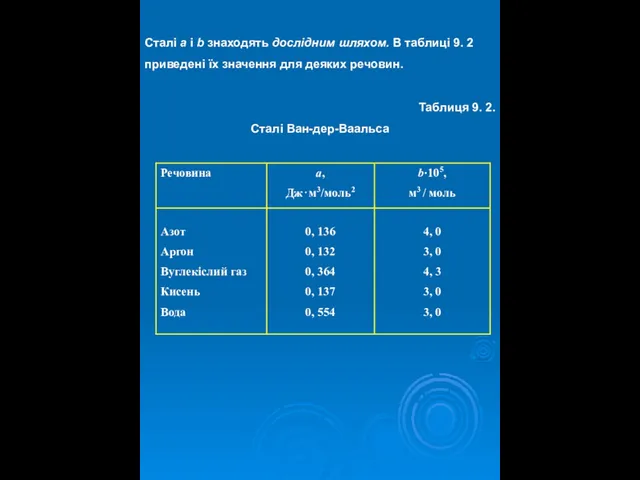
Сталі a і b знаходять дослідним шляхом. В таблиці 9. 2 приведені їх значення для деяких речовин.
Таблиця 9. 2.
Сталі Ван-дер-Ваальса

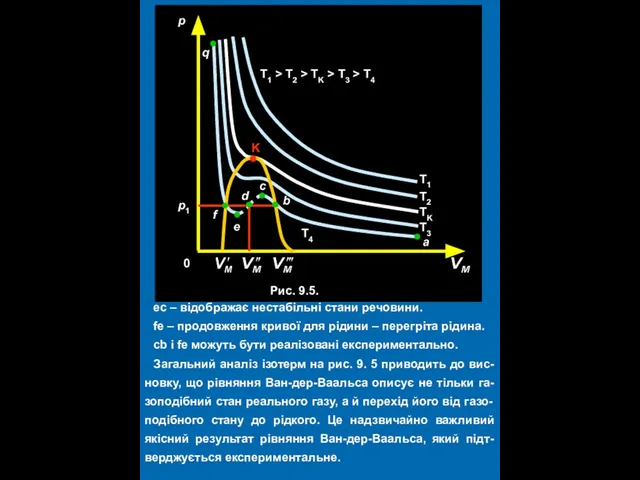
ес – відображає нестабільні стани речовини.
fе – продовження кривої для рідини – перегріта рідина.
сb і fe можуть бути реалізовані експериментально.
Загальний аналіз ізотерм на рис. 9. 5 приводить до вис-новку, що рівняння Ван-дер-Ваальса описує не тільки га-зоподібний стан реального газу, а й перехід його від газо-подібного стану до рідкого. Це надзвичайно важливий якісний результат рівняння Ван-дер-Ваальса, який підт-верджується експериментальне.
р
р1
0
K
T3
T4
TK
T2
T1
Рис. 9.5.
T1 > T2 > TK > T3 > T4
f
e
d
с
b
a
q

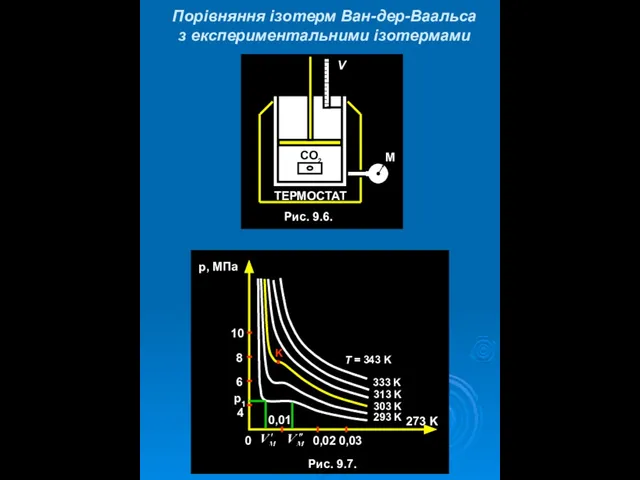
Порівняння ізотерм Ван-дер-Ваальса з експериментальними ізотермами