Relyatsionnaya_algebra

Реляционная алгебра – замкнутая система операций над отношениями в реляционной модели данных.
Группы операций
базовые теоретико-множественные;
специальные реляционные.
унарные;
бинарные.

Совместимость отношений
по типу
Два отношения являются совместимыми по типу, если они имеют идентичные заголовки:
множества имен атрибутов этих отношений совпадают;
атрибуты с одинаковыми именами определены на одном и том же домене.

Совместимость отношений по типу
ρНовоеОтношение(НовАтр1,…,НовАтрN)(СтароеОтношение)
<исходное отношение> RENAME <старое имя атрибута> AS <новое имя атрибута>
Для приведения отношений к одному типу следует использовать операцию переименования:
ρПоставщики (КодП, Имя, Город, Рейтинг)(S)
Поставщики RENAME Город_П AS Город_размещения _Поставщика

Операция множественного переименования
<отн.> RENAME <ст.имя атр.1> AS <нов.имя атр.1>,<ст.имя атр2> AS <нов.имя атр.2>, …, <ст.имя атрN> AS <нов.имя атр.N>

Теоретико-множественные операции

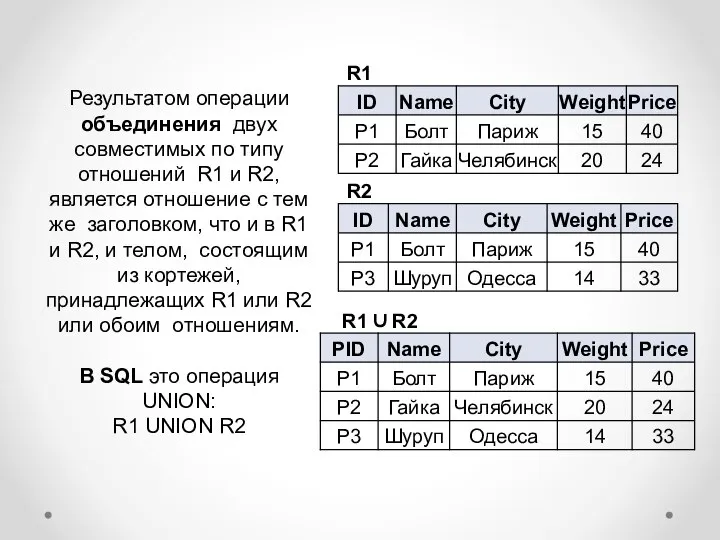
Результатом операции объединения двух совместимых по типу отношений R1 и R2, является отношение с тем же заголовком, что и в R1 и R2, и телом, состоящим из кортежей, принадлежащих R1 или R2 или обоим отношениям.
В SQL это операция UNION:
R1 UNION R2
R1
R2
R1 ∪ R2

Результатом операции пересечения двух совместимых по типу отношений R1 и R2 является отношение с тем же заголовком, что и в R1 и R2, и телом, состоящим из кортежей, принадлежащих обоим отношениям R1 и R2.
В SQL это операция INTERSECT:
R1 INTERSECT R2
R1 ∩ R2
R1
R2

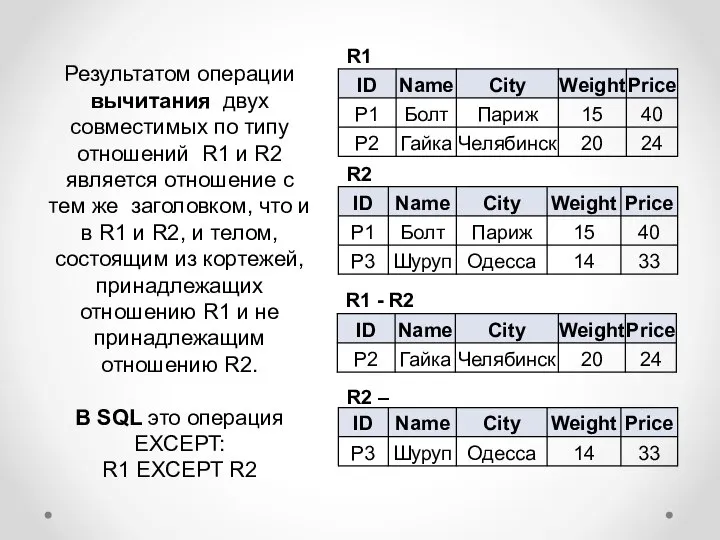
Результатом операции вычитания двух совместимых по типу отношений R1 и R2 является отношение с тем же заголовком, что и в R1 и R2, и телом, состоящим из кортежей, принадлежащих отношению R1 и не принадлежащим отношению R2.
В SQL это операция EXCEPT:
R1 EXCEPT R2
R2 – R1
R1 - R2
R1
R2

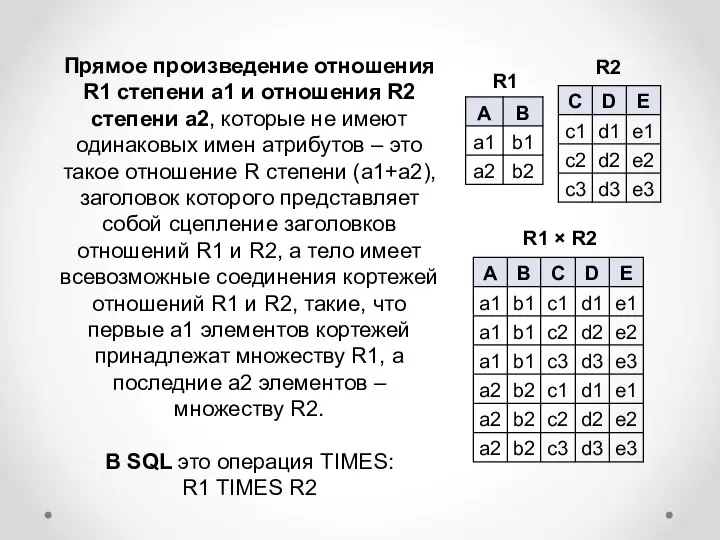
Прямое произведение отношения R1 степени a1 и отношения R2 степени a2, которые не имеют одинаковых имен атрибутов – это такое отношение R степени (a1+a2), заголовок которого представляет собой сцепление заголовков отношений R1 и R2, а тело имеет всевозможные соединения кортежей отношений R1 и R2, такие, что первые a1 элементов кортежей принадлежат множеству R1, а последние a2 элементов – множеству R2.
В SQL это операция TIMES:
R1 TIMES R2
R1
R1 × R2
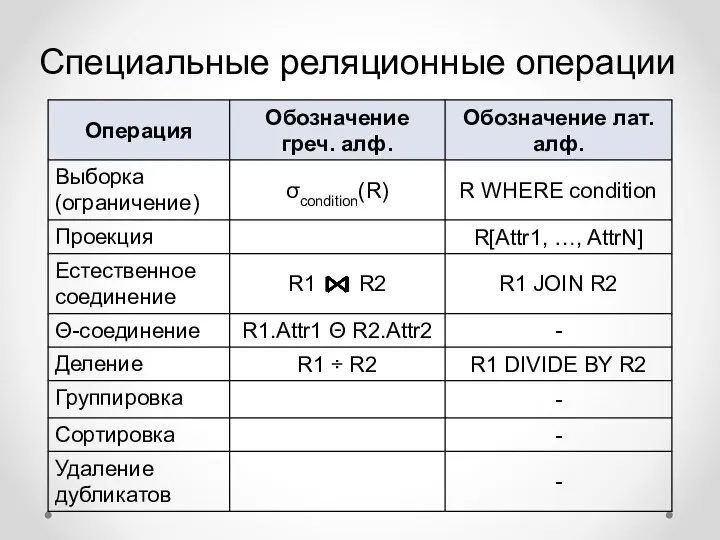
R2

Специальные реляционные операции

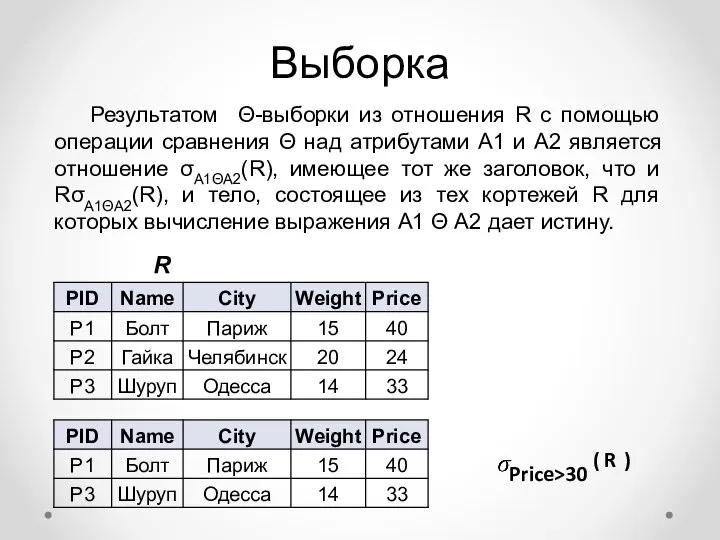
Выборка
Результатом Θ-выборки из отношения R с помощью операции сравнения Θ над атрибутами А1 и А2 является отношение σA1ΘA2(R), имеющее тот же заголовок, что и RσA1ΘA2(R), и тело, состоящее из тех кортежей R для которых вычисление выражения А1 Θ А2 дает истину.
R

Выборка по составному условию

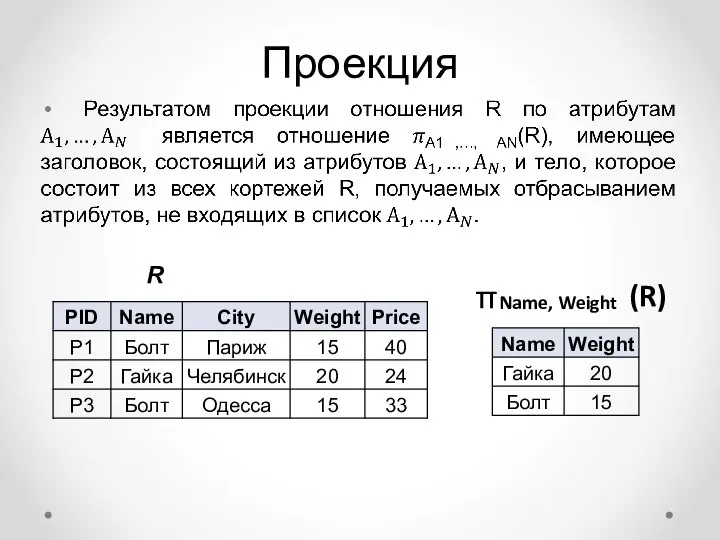
Проекция
R

Соединение
общая операция соединения;
Θ-соединение;
экви-соединение;
естественное соединение.

Общая операция соединения
Соединением отношений A и B по условию C называется отношение
(A TIMES B) WHERE C, где:
С – логическое выражение, в которое могут входить атрибуты отношений A и B и (или) скалярные выражения.

Θ-соединение
Пусть отношение A содержит атрибут X, отношение B – атрибут Y, а Θ – один из операторов сравнения. Тогда Θ – соединением отношения A по атрибуту X с отношением B по атрибуту Y называют отношение:
(A TIMES B) WHERE X Θ Y
(A TIMES B) WHERE X Θ Y
A
B

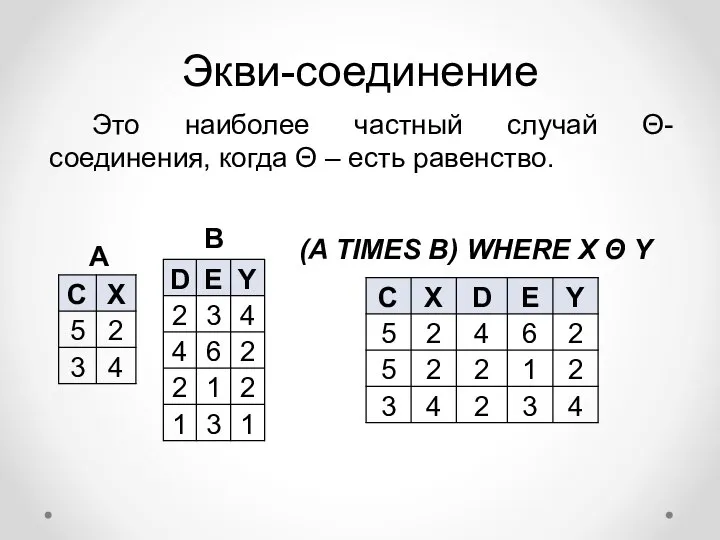
Экви-соединение
Это наиболее частный случай Θ-соединения, когда Θ – есть равенство.
(A TIMES B) WHERE X Θ Y
A
B

Естественное соединение
Результатом естественного соединения отношений R1(A,B) и R2(B,С) по общему атрибуту B является отношение R1 R2 с заголовком из атрибутов А, В, С, и телом, состоящим из соединенных кортежей, которые имеют совпадающие значения в общем атрибуте.
R1 R2
R1 R2 ≡ πA,B,C (σR1.B=R2.B(R1×R2))
R1
R2

Деление
Пусть имеются отношения А(X, Y) и В (Y), где атрибуты Y определены на одном и том же домене.
Тогда результатом деления A ÷ B будет отношение с заголовком из атрибута X и телом, в которое входят кортежи
такие, что существует кортеж
, который принадлежит отношению A для всех кортежей
из отношения В.

Деление

Деление