Содержание
- 2. Толковый словарь иностранных слов Л.П.Крысина СТАТИСТИКА [греч. statos стоящий; стоячий, неподвижный]. 1. Наука о количественных измерениях
- 3. Среднее арифметическое Мода Размах Медиана СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ
- 4. Среднее арифметическое ряда чисел - частное от деления суммы этих чисел на число слагаемых Задача: Сколько
- 5. Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду МОДА РЯДА ЧИСЕЛ
- 6. Какое число является модой данного ряда? 26 34 34 32 25 32 25 25 18 37
- 7. Размах ряда чисел - разность между наибольшим и наименьшим из этих чисел Пример: дан упорядоченный ряд
- 8. 26 34 34 32 25 32 25 25 18 37 20 23 25 РАЗМАХ РЯДА ЧИСЕЛ
- 9. Медианой упорядоченного ряда чисел с нечётным числом членов называется среднее в ряду число; с чётным числом
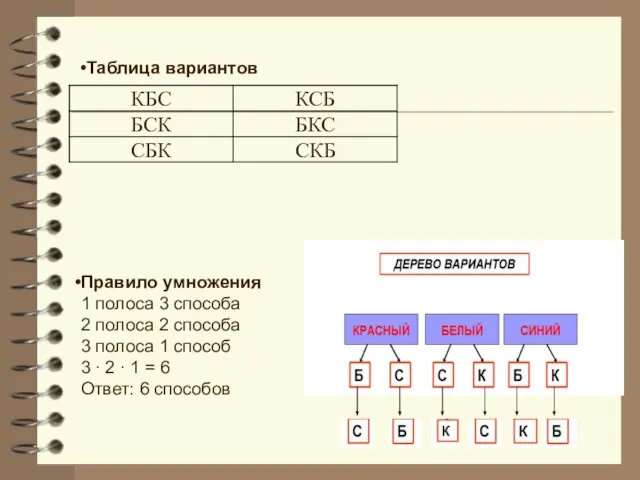
- 13. Таблица вариантов Правило умножения 1 полоса 3 способа 2 полоса 2 способа 3 полоса 1 способ
- 14. Пример 2.1. В кафе имеются 3 первых блюда. 5 вторых и 2 третьих. Сколькими способами посетитель
- 15. Пример 2.2. Двое размещаются в пустом купе. Сколькими способами они могут выбрать себе места. Решение. Представим
- 16. Пример 2.3. За круглый стол с 5-ю местами садятся 5 человек. а) Сколькими способами они могут
- 17. Пример 2.4. Представь, что у тебя 10 тюльпанов: 3 желтых, 2 оранжевых, 5 красных. Сколько и
- 19. Тест №5. В течении четверти Лена получила следующие отметки по алгебре: 3 двойки, 2 тройки, 4
- 20. Проверка теста №1. 4) 6 №2. 2) 13 №3. 1) 810 №4. 3)18 №5. 2) МОДА
- 21. Составить комбинаторные задачи практического содержания. Домашнее задание
- 22. Продолжите фразу: Сегодня на уроке… Теперь я знаю… - Мне на уроке… Итог урока
- 24. Скачать презентацию
![Толковый словарь иностранных слов Л.П.Крысина СТАТИСТИКА [греч. statos стоящий; стоячий, неподвижный]. 1.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/404936/slide-1.jpg)



















 THE CHRISTIAN WORKER
THE CHRISTIAN WORKER 1665678763032__30ro86
1665678763032__30ro86 Агрессия (4 класс)
Агрессия (4 класс) 1.1 + 1.2
1.1 + 1.2 История носового платка
История носового платка Поля листа
Поля листа Вкусное и красивое лакомство для неожиданных гостей
Вкусное и красивое лакомство для неожиданных гостей Добро пожаловать
Добро пожаловать Независимое распределение затрат в управленческом и регламентированном учете
Независимое распределение затрат в управленческом и регламентированном учете Абсолютные показатели оценки риска
Абсолютные показатели оценки риска Кипение
Кипение Страны Северной Европы
Страны Северной Европы Конструкция головы человека и её пропорции (6 класс)
Конструкция головы человека и её пропорции (6 класс) Энтеровирусная инфекция
Энтеровирусная инфекция Конвекция
Конвекция САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ
САНИТАРНО-ЭПИДЕМИОЛОГИЧЕСКИЕ ТРЕБОВАНИЯ К УСЛОВИЯМИ ОРГАНИЗАЦИИ ОБУЧЕНИЯ В ОБЩЕОБРАЗОВАТЕЛЬНЫХ УЧРЕЖДЕНИЯХ Ассоциация «МЫ»
Ассоциация «МЫ» Диагностика автомобиля. Диагностирование осветительных приборов
Диагностика автомобиля. Диагностирование осветительных приборов Денис Васильевич Давыдов
Денис Васильевич Давыдов Рекомендую как пособие по медицинской генетике
Рекомендую как пособие по медицинской генетике Любимый семейный завтрак семьи Пьянковых
Любимый семейный завтрак семьи Пьянковых Доброта
Доброта О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ
О РЕЗУЛЬТАТАХ ЕГЭ в г. Сочи в 2011 ГОДУ Психологические закономерности формирования личности в тренировочном процессе.
Психологические закономерности формирования личности в тренировочном процессе. Базовый межшкольный методический центр 26311
Базовый межшкольный методический центр 26311 Сложение и вычитание двузначных чисел 2 класс
Сложение и вычитание двузначных чисел 2 класс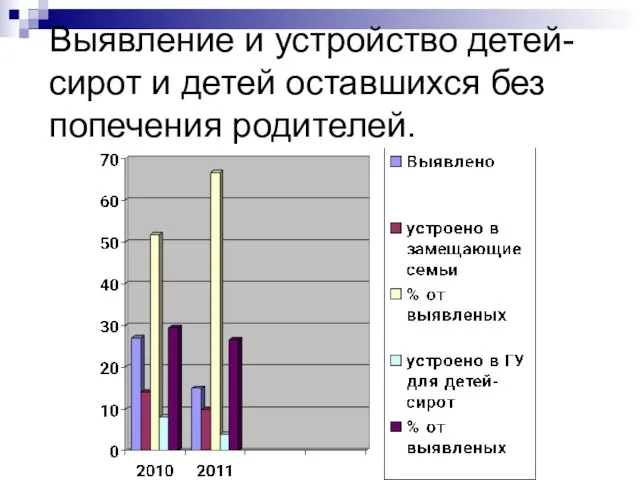 Выявление и устройство детей-сирот и детей оставшихся без попечения родителей.
Выявление и устройство детей-сирот и детей оставшихся без попечения родителей. Создание единого китайского государства
Создание единого китайского государства