Содержание
- 2. Вопрос: Что такое задача?
- 3. Ответ: В задаче по известным данным надо найти неизвестное.
- 4. Задача Расстояние между двумя пунктами по реке равно 21 км. Лодка проходит этот путь по течению
- 5. Вопрос Как решить данную задачу?
- 6. Ответ С помощью системы уравнений. Если поставлена задача найти такие пары чисел (х;у), которые одновременно удовлетворяют
- 7. Запишем математическую модель: Пусть х - у - Тогда по течению лодка пройдет а против течения
- 8. Вопрос Обязательно ли неизвестную величину обозначать буквой х?
- 9. Ответ Нет. Можно использовать любую букву. Всё зависит от того, что надо найти. Например, в данной
- 10. Вернемся к нашей задаче и проверим математическую модель: Пусть х – скорость лодки, у - скорость
- 11. Решим систему: 3(х+у) = 21 4,2 (х-у) =21
- 12. х+у = 7 х-у =5 2х = 12 х = 6 у = 1 Ответ: 6
- 13. Решите самостоятельно Найдите двузначное число, которое в 4 раза больше суммы своих цифр и в 3
- 14. 2. Решите систему: а + b = 6 ab = 5
- 16. Скачать презентацию













 Олимпийские игры в Греции 5 класс
Олимпийские игры в Греции 5 класс Поколение ЭВМ
Поколение ЭВМ ИКТ в системе работы с одаренными детьми
ИКТ в системе работы с одаренными детьми Histoire de Disneyland Paris
Histoire de Disneyland Paris Химическая связь
Химическая связь Вещное право в МЧП. Тема 8
Вещное право в МЧП. Тема 8 Где получить профессию финансиста?
Где получить профессию финансиста?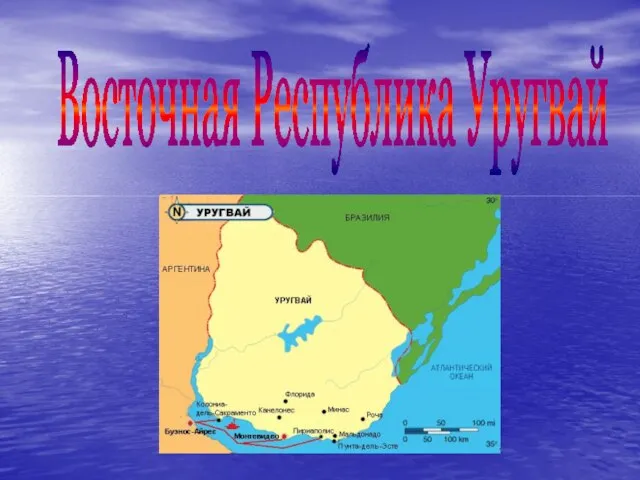 Презентация на тему Уругвай
Презентация на тему Уругвай Презентация без названия
Презентация без названия Модели данных
Модели данных  Письмо заглавной буквы Ж
Письмо заглавной буквы Ж Повторение изученного
Повторение изученного Музеи искусства. Картина-пейзаж
Музеи искусства. Картина-пейзаж Две стратегии повышения эффективности контекстной рекламы Андрей Лебедев , Зураб Полосин, интернет-маркетологи департамента Ин
Две стратегии повышения эффективности контекстной рекламы Андрей Лебедев , Зураб Полосин, интернет-маркетологи департамента Ин Презентация на тему Социальный прогресс и развитие общества 8 КЛАСС
Презентация на тему Социальный прогресс и развитие общества 8 КЛАСС Презентация на тему Причастие как часть речи (7 класс)
Презентация на тему Причастие как часть речи (7 класс) Деньги Money
Деньги Money Презентация на тему Начало Реформации в Европе
Презентация на тему Начало Реформации в Европе  Презентация на тему Архитектура классицизма в России МХК 11 класс
Презентация на тему Архитектура классицизма в России МХК 11 класс  Налогообложение и социальная политика РФ.
Налогообложение и социальная политика РФ. Групповая дифференциация и лидерство
Групповая дифференциация и лидерство Теория цвета
Теория цвета Гуморальная регуляция автономных функций
Гуморальная регуляция автономных функций Презентація
Презентація Порахуй з Вовком!
Порахуй з Вовком! Производство Наноструктурированного пенобетона
Производство Наноструктурированного пенобетона Система защиты труб от замерзания
Система защиты труб от замерзания Презентация на тему Развитие связной речи у дошкольников Советы родителям
Презентация на тему Развитие связной речи у дошкольников Советы родителям