Вписанные и описанные многогранники

Цель работы состоит в том, чтобы узнать весь теоретический материал по теме «Вписанные и описанные многогранники» и научиться применять его на практике.
Цель реферата

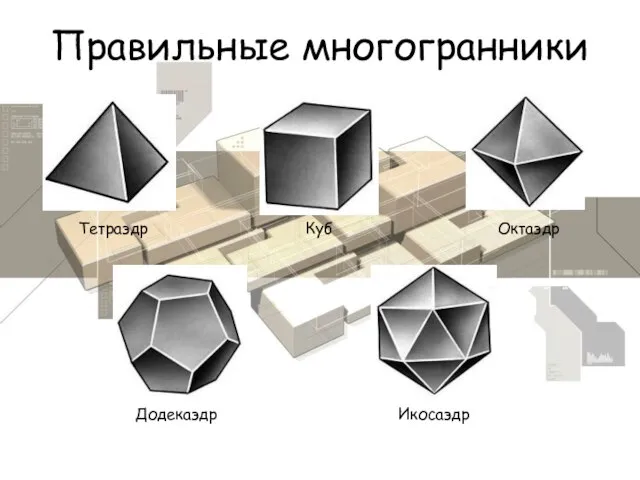
Правильные многогранники
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр

Многогранники, вписанные в шар
Выпуклый многогранник называется вписанным, если все его вершины лежат на некоторой сфере. Эта сфера называется описанной для данного многогранника. Центр этой сферы является точкой, равноудаленной от вершин многогранника. Она является точкой пересечения плоскостей, каждая из которых проходит через середину ребра многогранника перпендикулярно ему.

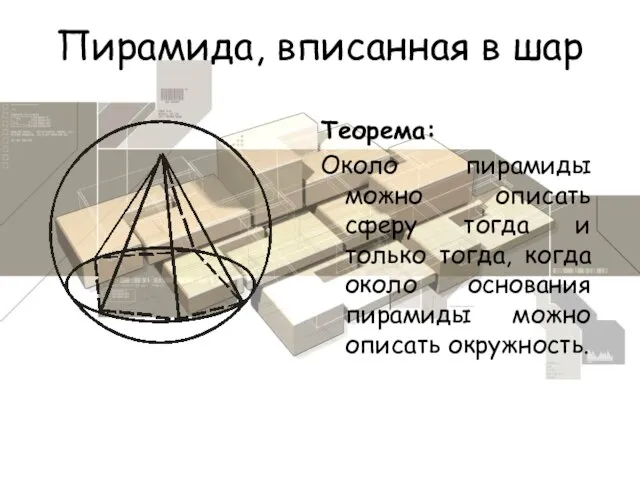
Пирамида, вписанная в шар
Теорема:
Около пирамиды можно описать сферу тогда и только тогда, когда около основания пирамиды можно описать окружность.

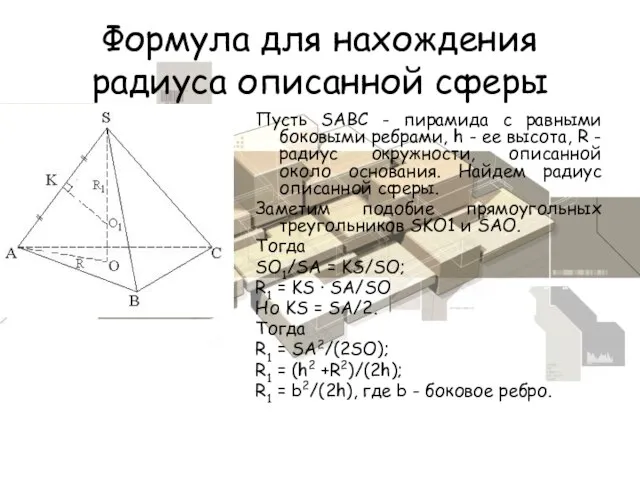
Формула для нахождения радиуса описанной сферы
Пусть SABC - пирамида с равными боковыми ребрами, h - ее высота, R - радиус окружности, описанной около основания. Найдем радиус описанной сферы.
Заметим подобие прямоугольных треугольников SKO1 и SAO.
Тогда
SO1/SA = KS/SO;
R1 = KS · SA/SO
Но KS = SA/2.
Тогда
R1 = SA2/(2SO);
R1 = (h2 +R2)/(2h);
R1 = b2/(2h), где b - боковое ребро.

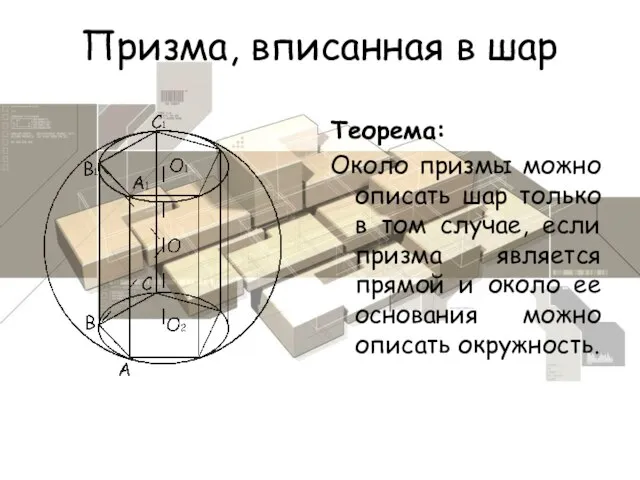
Призма, вписанная в шар
Теорема:
Около призмы можно описать шар только в том случае, если призма является прямой и около ее основания можно описать окружность.

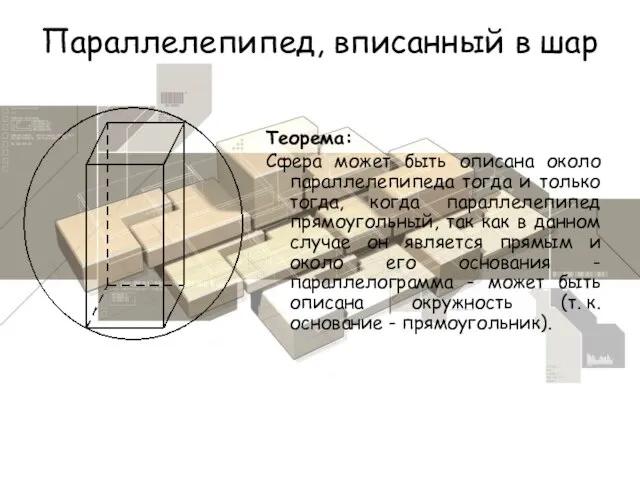
Параллелепипед, вписанный в шар
Теорема:
Сфера может быть описана около параллелепипеда тогда и только тогда, когда параллелепипед прямоугольный, так как в данном случае он является прямым и около его основания - параллелограмма - может быть описана окружность (т. к. основание - прямоугольник).

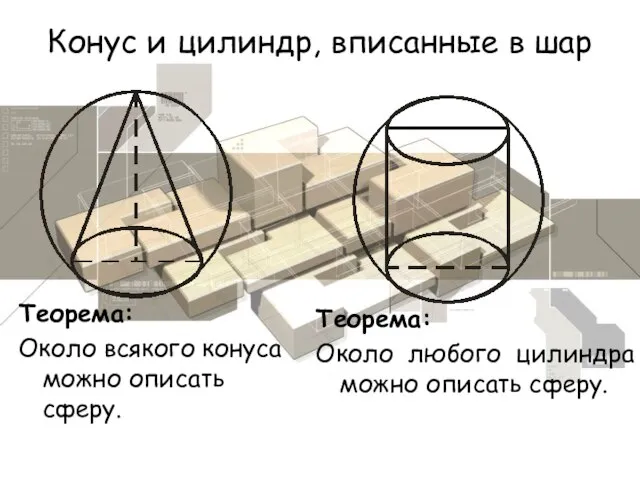
Конус и цилиндр, вписанные в шар
Теорема:
Около всякого конуса можно описать сферу.
Теорема:
Около любого цилиндра можно описать сферу.

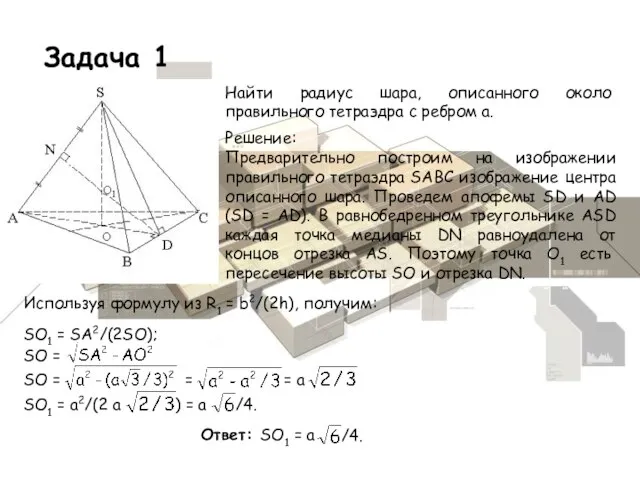
Задача 1
Найти радиус шара, описанного около правильного тетраэдра с ребром а.
Решение:
SO1 = SA2/(2SO);
SO =
SO =
=
= a
SO1 = a2/(2 a
) = a
/4.
Ответ:
SO1 = a
/4.
Предварительно построим на изображении правильного тетраэдра SABC изображение центра описанного шара. Проведем апофемы SD и AD (SD = AD). В равнобедренном треугольнике ASD каждая точка медианы DN равноудалена от концов отрезка AS. Поэтому точка O1 есть пересечение высоты SO и отрезка DN.
Используя формулу из R1 = b2/(2h), получим:

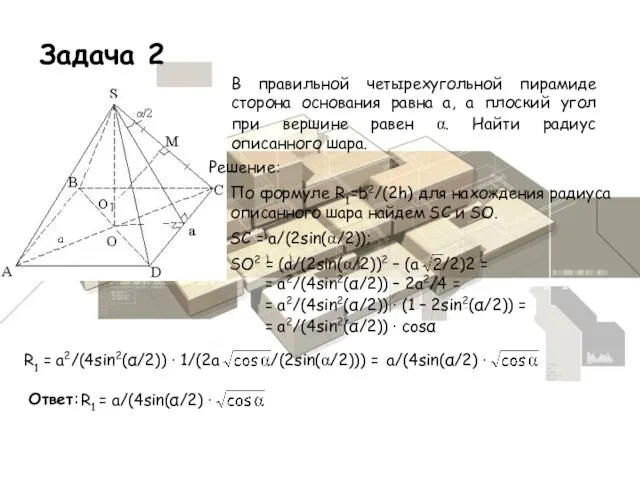
Задача 2
Решение:
По формуле R1=b2/(2h) для нахождения радиуса описанного шара найдем SC и SO.
SC = a/(2sin(α/2));
SO2 = (a/(2sin(α/2))2 – (a
/2)2 =
= a2/(4sin2(α/2)) – 2a2/4 =
= a2/(4sin2(α/2)) · (1 – 2sin2(α/2)) =
= a2/(4sin2(α/2)) · cosα
В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найти радиус описанного шара.
R1 = a2/(4sin2(α/2)) · 1/(2a
/(2sin(α/2))) =
a/(4sin(α/2) ·
).
Ответ:
R1 = a/(4sin(α/2) ·
).

Многогранники, описанные около шара
Выпуклый многогранник называется описанным, если все его грани касаются некоторой сферы. Эта сфера называется вписанной для данного многогранника. Центром вписанной сферы является точка, равноудаленная от всех граней многогранника.

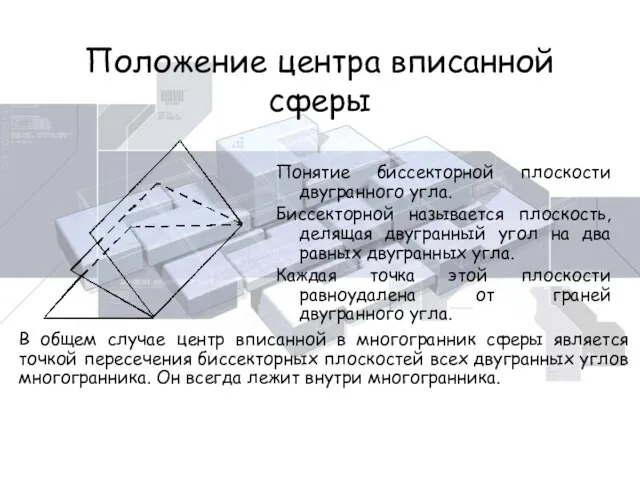
Положение центра вписанной сферы
Понятие биссекторной плоскости двугранного угла.
Биссекторной называется плоскость, делящая двугранный угол на два равных двугранных угла.
Каждая точка этой плоскости равноудалена от граней двугранного угла.
В общем случае центр вписанной в многогранник сферы является точкой пересечения биссекторных плоскостей всех двугранных углов многогранника. Он всегда лежит внутри многогранника.

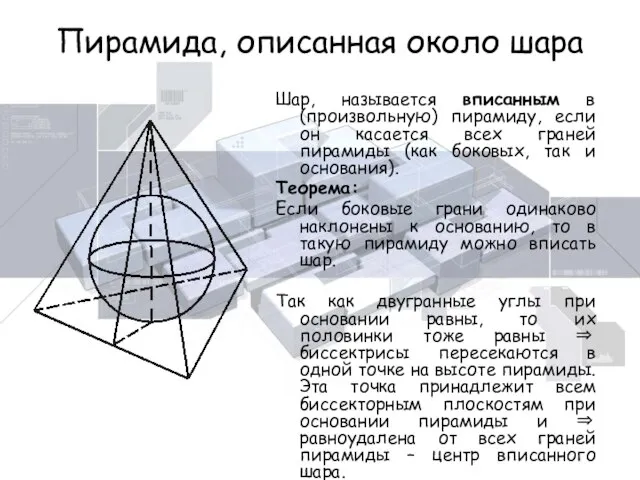
Пирамида, описанная около шара
Шар, называется вписанным в (произвольную) пирамиду, если он касается всех граней пирамиды (как боковых, так и основания).
Теорема:
Если боковые грани одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.
Так как двугранные углы при основании равны, то их половинки тоже равны ⇒ биссектрисы пересекаются в одной точке на высоте пирамиды. Эта точка принадлежит всем биссекторным плоскостям при основании пирамиды и ⇒ равноудалена от всех граней пирамиды – центр вписанного шара.

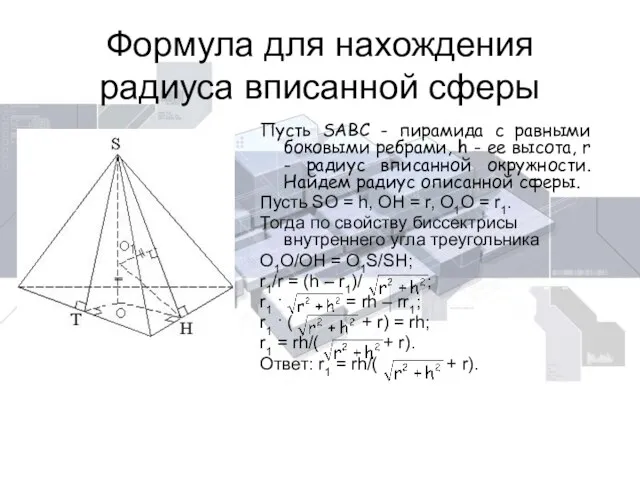
Формула для нахождения радиуса вписанной сферы
Пусть SABC - пирамида с равными боковыми ребрами, h - ее высота, r - радиус вписанной окружности. Найдем радиус описанной сферы.
Пусть SO = h, OH = r, O1O = r1.
Тогда по свойству биссектрисы внутреннего угла треугольника
O1O/OH = O1S/SH;
r1/r = (h – r1)/ ;
r1 · = rh – rr1;
r1 · ( + r) = rh;
r1 = rh/( + r).
Ответ: r1 = rh/( + r).

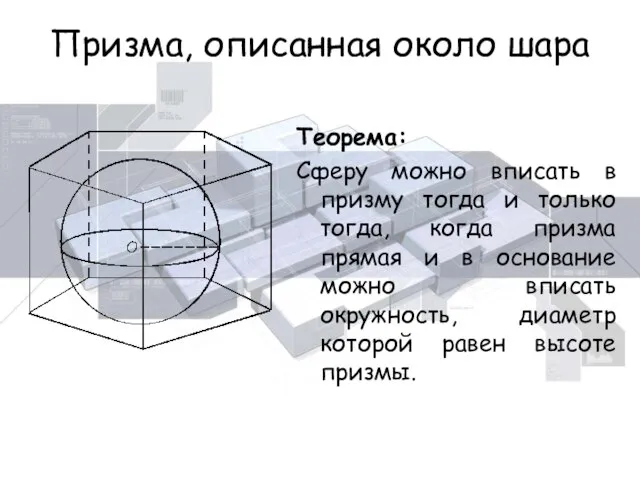
Призма, описанная около шара
Теорема:
Сферу можно вписать в призму тогда и только тогда, когда призма прямая и в основание можно вписать окружность, диаметр которой равен высоте призмы.

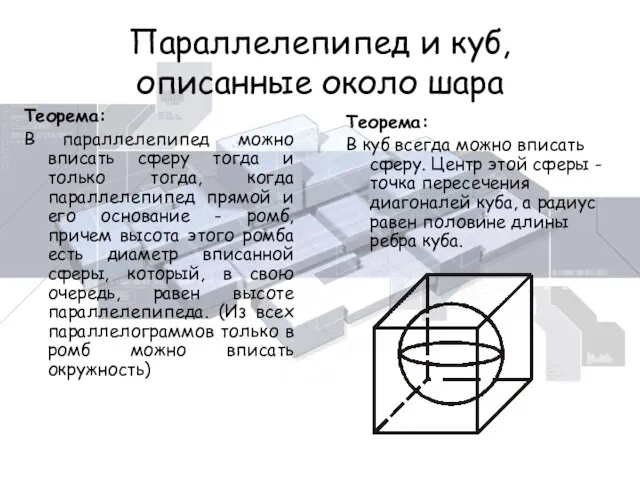
Параллелепипед и куб, описанные около шара
Теорема:
В параллелепипед можно вписать сферу тогда и только тогда, когда параллелепипед прямой и его основание - ромб, причем высота этого ромба есть диаметр вписанной сферы, который, в свою очередь, равен высоте параллелепипеда. (Из всех параллелограммов только в ромб можно вписать окружность)
Теорема:
В куб всегда можно вписать сферу. Центр этой сферы - точка пересечения диагоналей куба, а радиус равен половине длины ребра куба.

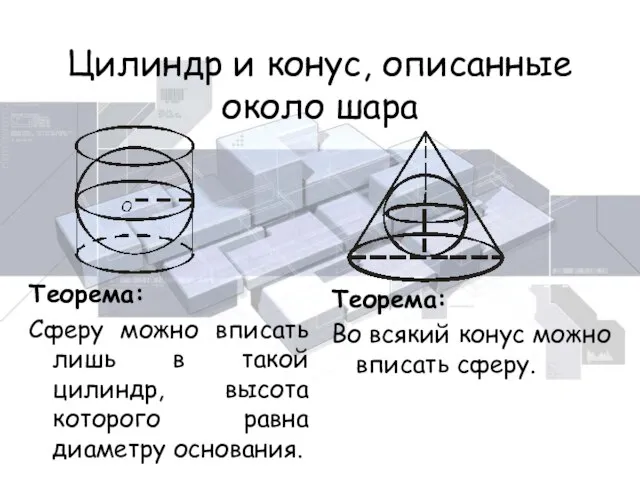
Цилиндр и конус, описанные около шара
Теорема:
Сферу можно вписать лишь в такой цилиндр, высота которого равна диаметру основания.
Теорема:
Во всякий конус можно вписать сферу.

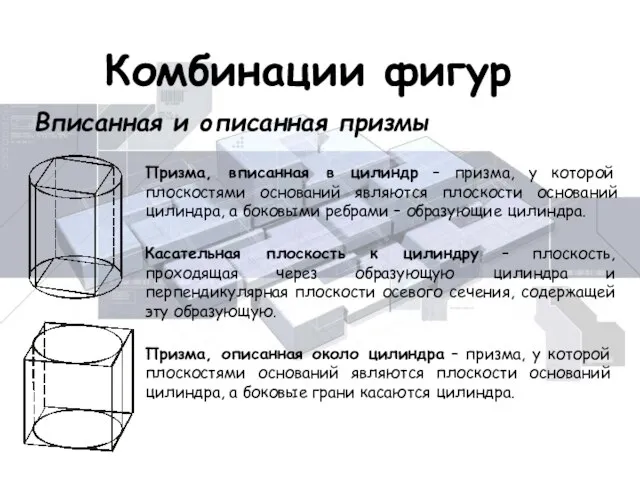
Комбинации фигур
Вписанная и описанная призмы
Призма, описанная около цилиндра – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковые грани касаются цилиндра.
Призма, вписанная в цилиндр – призма, у которой плоскостями оснований являются плоскости оснований цилиндра, а боковыми ребрами – образующие цилиндра.
Касательная плоскость к цилиндру – плоскость, проходящая через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.

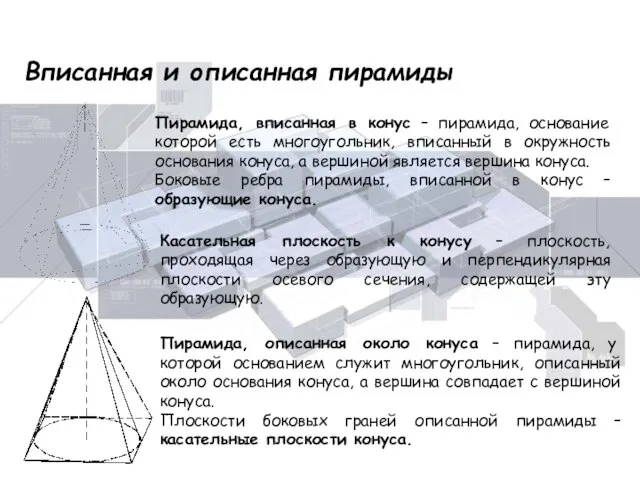
Вписанная и описанная пирамиды
Пирамида, вписанная в конус – пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, а вершиной является вершина конуса.
Боковые ребра пирамиды, вписанной в конус – образующие конуса.
Пирамида, описанная около конуса – пирамида, у которой основанием служит многоугольник, описанный около основания конуса, а вершина совпадает с вершиной конуса.
Плоскости боковых граней описанной пирамиды – касательные плоскости конуса.
Касательная плоскость к конусу – плоскость, проходящая через образующую и перпендикулярная плоскости осевого сечения, содержащей эту образующую.

Другие виды конфигураций
Цилиндр вписан в пирамиду, если окружность одного его основания касается всех боковых граней пирамиды, а другое его основание лежит на основании пирамиды.
Конус вписан в призму, если его вершина лежит на верхнем основании призмы, а его основание – круг, вписанный в многоугольник – нижнее основание призмы.
Призма вписана в конус, если все вершины верхнего основания призмы лежат на боковой поверхности конуса, а нижнее основание призмы лежит на основании конуса.

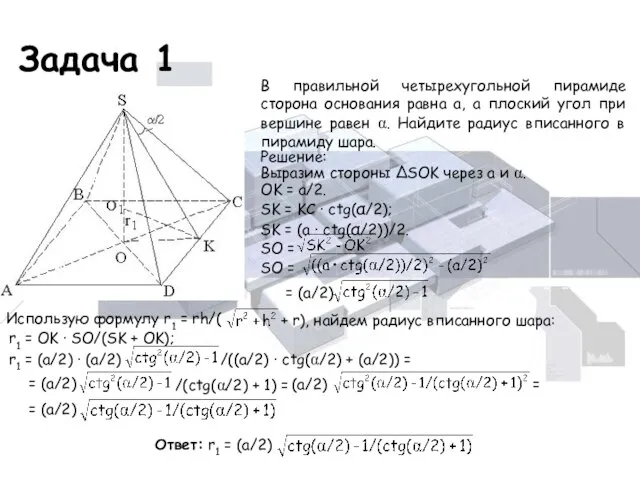
Задача 1
В правильной четырехугольной пирамиде сторона основания равна а, а плоский угол при вершине равен α. Найдите радиус вписанного в пирамиду шара.
Решение:
Выразим стороны ∆SOK через а и α.
OK = a/2.
SK = KC · ctg(α/2);
SK = (a · ctg(α/2))/2.
SO =
SO =
= (a/2)
Использую формулу r1 = rh/(
+ r), найдем радиус вписанного шара:
r1 = OK · SO/(SK + OK);
r1 = (a/2) · (a/2)
/((a/2) · ctg(α/2) + (a/2)) =
= (a/2)
/(ctg(α/2) + 1) =
(a/2)
=
= (a/2)
Ответ: r1 = (a/2)