Session 1.2_Time Value of Money

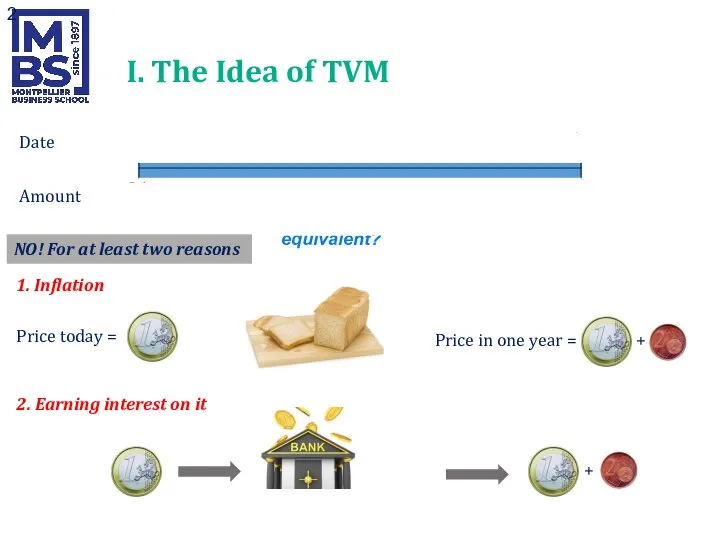
I. The Idea of TVM
€ 1
Date
Amount
0 (today)
€ 1
1 (end of the year)
1. Inflation
2. Earning interest on it
2%
NO! For at least two reasons

A project (= an investment) that will generate one cash flow in one year:
I. The Idea of TVM
Date
Amount
Cost = € 1000
0 (today)
€ 1020
1 (end of the year)
If the current interest rate is 5%, will you accept to invest € 1000 today in this project?
To decide, compare
The value of cash-flow from the project
today
The cost of the project
today
If the value of cash inflow today > The cost ? Accept
If not ? Reject
Take into account the time value of money to decide

I. The Idea of TVM
How can I obtain the value today (the present value) of a future cash flow?
If the project will generate cash flows over N periods in the future
How to obtain the present value of cash flows?
CF0
0
1
2
3
…....
N
CF1
CF2
CFN
CF3
N-1
CFN-1
…....
What if all the future cash flows are equal? What if we have an infinite number of cash flows?
? Tools to evaluate cash flows lasting several periods.
? We develop these tools in this session.

II. The Three Rules of Time Travel
Financial decisions ? Comparing or combining cash flows that occur at different points in time.
? Three important rules:
Rule 1: Comparing and Combining Values
It is only possible to compare or combine values at the same point in time.

II. The Three Rules of Time Travel
Rule 2: Moving Cash Flows Forward in Time
Suppose we have € 1000 today, and we wish to determine the equivalent amount in one year’s time.
If the current interest rate is 10%, we move the cash flow forward in time as follows:
€1000 × (1+0.1) = €1100 in one year
In general, if the market interest rate is r
CF today × (1+r) ? Move the cash flow from the beginning to the end of the year
0 (beginning of the year)
1 (end of the year)
CF
CF × (1+r)
Compounding

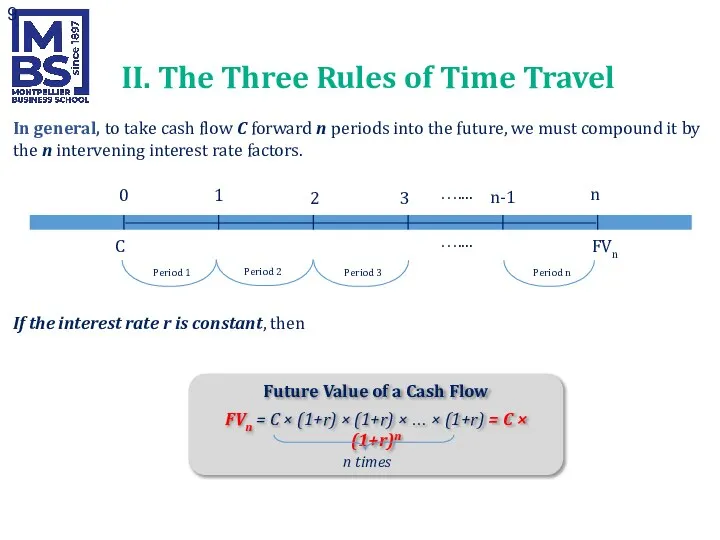
II. The Three Rules of Time Travel
0
1
2
€ 1000
€ 1100
€ 1210
× (1+0.1)
× (1+0.1)
How much the € 1000 is worth in two years’ time?
? If the interest rate for year 2 is also 10%, then
? Given a 10% interest rate, all of the cash flows (€1000 at date 0, €1100 at date 1, and €1210 at date 2) are equivalent: They have the same value but are expressed in different points in time.
The value of a cash flow that is moved forward in time is known as its future value.
Compound interest: Earning ‘interest on interest’.

0
1
2
€ 1000
€ 1100
€ 1210
× (1+0.1)
× (1+0.1)
? If we move the cash flow two years, we obtain: €1000 × (1.10)² = € 1210
0
1
2
3
€ 1000
€ 1100
€ 1210
€ 1331
× (1+0.1)
× (1+0.1)
× (1+0.1)
Over 3 years?
? If we move the cash flow three years, we obtain: €1000 × (1.10)3 = € 1331
II. The Three Rules of Time Travel

In general, to take cash flow C forward n periods into the future, we must compound it by the n intervening interest rate factors.
If the interest rate r is constant, then
II. The Three Rules of Time Travel
C
0
1
2
3
…....
n
FVn
n-1
…....

II. The Three Rules of Time Travel
Exercise 1
Suppose you invest €1000 in an account paying 10% interest per year. How much will you have in the account in 7 years and in 75 years?
Solution
7 years: €1000 × (1.10)7 = €1948.72 ? Your money nearly double.
75 years: €1000 × (1.10)75 = €1,271,895.37 ? You will be a millionaire!

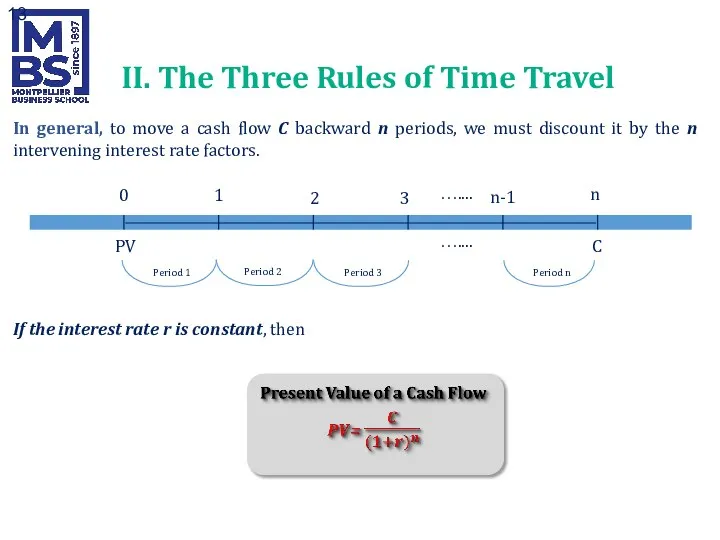
Rule 3: Moving Cash Flows Back in Time
Suppose you would like to compute the value today of €1000 you anticipate receiving in one year.
If the current market interest rate is 10%, you can compute this value as follows:
II. The Three Rules of Time Travel
? To move the cash flow backward in time, we divide it by the interest rate factor, (1+r), where r is the interest rate.
? This process of moving a value or cash flow backward in time is known as discounting.

0
1
2
€ 826.45
€ 909.09
€ 1000
/1.10
/1.10
II. The Three Rules of Time Travel
Suppose you would like to compute the value today of €1000 you anticipate receiving in two years.
If the current market interest rate is 10%, you can compute this value as follows:
The value of a future cash flow at an earlier point on the timeline is its present value at the earlier point in time.

In general, to move a cash flow C backward n periods, we must discount it by the n intervening interest rate factors.
If the interest rate r is constant, then
PV
0
1
2
3
…....
n
C
n-1
…....
II. The Three Rules of Time Travel

Exercise 2
You are considering investing in a savings bond that will pay €15 000 in 10 years. If the competitive market interest rate is fixed at 6% per year, what is the bond worth today?
?
0
1
2
3
10
€15 000
9
Solution
…
II. The Three Rules of Time Travel

Applying the Rules of Time Travel
The rules of time travel allow us to compare and combine cash flows that occur at different points in time. Suppose we plan to save €1000 today, and €1000 at the end of each of the next two years.
If we earn a fixed 10% interest rate on our savings, how much will we have three years from today?
0
1
2
3
€ 1000
€ 1000
€ 1000
?
Solution
€ 1000*1.13 + € 1000*1.12 + € 1000*1.1 = € 3641
II. The Three Rules of Time Travel

III. Valuing a stream of Cah Flows
Consider a stream of cash flows: C0 at date 0; C1 at date 1, and so on, up to CN at date N. We present this cash flow stream on a timeline as follows:
C0
0
1
2
N
CN
………………………
C2
C1