Система подготовки учащихся к Е Г Э(из опыта работы учителей Республики Бурятия)

Цель:
Исходя из опыта работы, а также результатов ЕГЭ в 2004-2005 учебном году, помочь коллегам-учителям наиболее эффективно подготовить учащихся-выпускников школ к успешной сдаче ЕГЭ по математике.

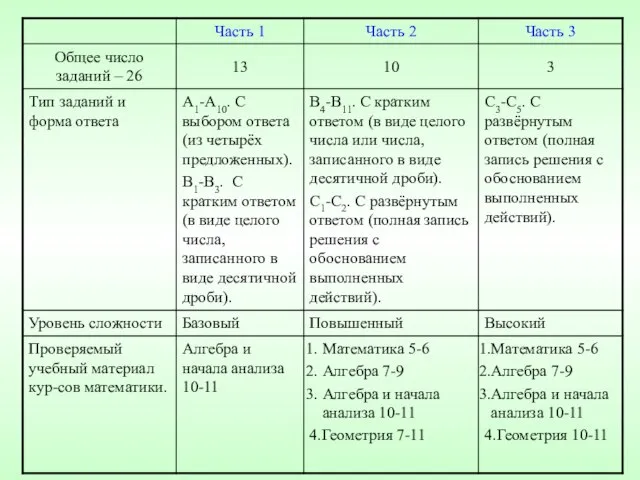
План
Цель проведения ЕГЭ.
Структура экзаменационной работы.
Шкала оценок и система оценивания работы учащегося.
Тестирование как способ мониторинга знаний.
Психологическая подготовка к ЕГЭ
Техническая подготовка к ЕГЭ.
Методическая подготовка к ЕГЭ.
Тематическое планирование занятий.
Методические разработки отдельных тем.
Методика работы с заданиями, содержащими модуль.
Уравнения и неравенства с модулем. Системы.
Выражения и преобразования. Функции
Геометрические фигуры и их свойства. Измерение
геометрических величин.
О результатах ЕГЭ выпускников лингв. Гимназии №3
(Учитель Баханова Л. И.) и Кяхтинской СОШ №2 (Учитель Булыгина Т.Г.)
11. Список литературы.

Цель ЕГЭ – совместить в себе два экзамена – выпускной за среднюю школу и вступительный в ВУЗы. В соответствие с целью в ЕГЭ проверяется владение материалом курса алгебры и начал анализа 10 – 11 классов, а также материалом, из которых часто составляются задания на вступительных экзаменах в ВУЗы.
Общее число заданий в работе в 2005году – 26. Время на выполнение работы – 4 часа.
Работа состоит из трёх частей:
Часть 1 – задания обязательного уровня сложности.
Часть 2 – задания повышенного уровня сложности.
Часть 3 – задания высокого уровня сложности.

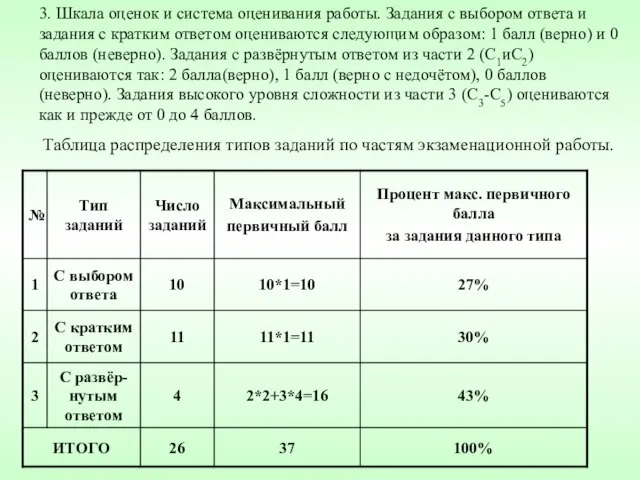
3. Шкала оценок и система оценивания работы. Задания с выбором ответа и задания с кратким ответом оцениваются следующим образом: 1 балл (верно) и 0 баллов (неверно). Задания с развёрнутым ответом из части 2 (C1иС2) оцениваются так: 2 балла(верно), 1 балл (верно с недочётом), 0 баллов (неверно). Задания высокого уровня сложности из части 3 (С3-С5) оцениваются как и прежде от 0 до 4 баллов.
Таблица распределения типов заданий по частям экзаменационной работы.

Проверка ответов к заданиям 1 и 2 проводится на компьютере. Проверка ответов к заданиям с развёрнутым ответом осуществляется экспертной комиссией, в составе которой находятся учителя, методисты и работники ВУЗов.
Задание с выбором ответа выполнено верно, если в бланке ответов обозначена правильная цифра, обозначающая ответ на данное задание.
Задание с кратким ответом (ответ всегда либо целое число, либо десятичная дробь) выполнено верно, если в бланке ответов записано это число.
Аттестационная оценка выпускника школы определяется по 5-балльной шкале на основе выполнения 22-х заданий (выполнение заданий B9, B10, B11, C4 не учитывается).
Тестовая оценка выставляется по 100-балльной шкале на основе выполнения всех 26 заданий работы. Тестовая оценка в отличие от аттестационной служит цели определения степени готовности выпускника к поступлению и учёбе в ВУЗе. Аттестационная оценка и тестовая – две разные оценки и служат различным целям.
10.06.2005г. вышло распоряжение Федеральной службы по надзору в сфере образования и науки № 943-08.

Установить шкалу перевода баллов в отметки при проведении ЕГЭ по алгебре и началам анализа и по математике:
По алгебре и началам анализа
0-5 заданий – «2»
6-11 заданий – «3»
12-18 заданий – «4»
19-30 заданий – «5»
По математике
0-37 баллов - «2»
38-55 баллов - «3»
56-74 балла - «4»
75 и более - «5»
Руководитель : В.А. Болотов
Выписка из РАСПОРЯЖЕНИЯ № 943-08 от 10.06.2005 «Об установлении шкалы перевода баллов в отметки при проведении ЕГЭ по математике»

Слово «test» (тест) в переводе с английского означает задачу, испытание. Тестирование – целенаправленное, одинаковое для всех испытуемых обследование, проводимое в строго контролируемых условиях, позволяющее объективно измерять изучаемые характеристики педагогического процесса. От других способов обследования тестирование отличается точностью, простотой, доступностью, возможностью автоматизации.
Таким образом, решаются три основных положения (подчёркнутые) в процессе тестирования.
Но есть и оборотная сторона такой организации мониторинга знаний:
нерегулярность (эпизодичность) обратной связи (всего лишь дважды: пробный и основной экзамен);
неполный охват проверкой содержания, хотя количество заданий достаточно велико;
отсутствие проверки процесса работы ученика. (лишь в части С)

Психологическая подготовка к ЕГЭ
Следует учить школьника «технике сдачи теста»:
обучение жесткому самоконтролю времени
обучение оценки трудности заданий и разумному выбору этих заданий
обучение прикидке границ результатов
обучение приему «спирального движения по тексту»
Например, тот ученик , который планирует получить оценку «5», должен 1-ю
часть выполнить за 40-45 мин., во 2-й части – еще 1 час, в 3-й части – 1-1,5
часа. Остальное время нужно потратить на повторную проверку, грамотные
записи.
Выдержать 3,5-4 часа без перерыва при этом не может большинство
школьников. Поэтому к такому режиму надо приучать учеников хотя бы 1 раз
в неделю.
При тематическом выборе заданий нужно детей ориентировать на те задания,
где работают универсальные приемы решения, например, при решении
показательных уравнений или заданий , связанных с логарифмами.
То есть, наша задача подготовить школьника так, чтобы он самостоятельно
сумел набрать максимально возможное для него количество баллов.

Техническая подготовка к ЕГЭ
При выполнении заданий A и B учить школьников не выполнять задания полностью письменно, как можно больше преобразований в уме, поменьше записей, что сэкономит время. Статистика показывает, что не более 10% учащихся выполняют задания C, поэтому с такими учащимися лучше заниматься факультативно. Однако 1-2 задания могут быть посильны и учащимся, претендующими на «4».

Принципы построения методической подготовки
Тематический принцип с соблюдением «правила спирали» - от простых типовых до заданий раздела С.
Логическая взаимосвязь системы тестовых заданий.
Тренировочные тесты в режиме «теста скорости», т.е. с жестким ограничением времени, помнить о том, что интеллект, как и мышцы, нужно тренировать.
Принцип максимализации нагрузки как по содержанию, так и по времени для всех школьников в равной мере.
Переход к комплексным тестам разумен только в конце подготовки (апрель-май), проведение пробного ЕГЭ.
Уметь максимально использовать запас знаний, применяя различные «хитрости» и «правдоподобные рассуждения» для получения ответа простым и быстрым способом.

Пример:
Найти наименьшее значение функции. Можно, конечно исследовать функцию с помощью производной, т.е. пойти стандартным путем.
Выполним рисунок
для g(x)=9-x2 , max g(x)=g(0)=9, значит min f(x)=f(0)=-2,
т.е. ; f(x)-убывающая функция.
Особое внимание следует уделить наиболее слабым местам в знаниях школьников: корни, модули, параметры, исследование функций, иррациональность во всех вариантах, в т.ч. с модулями, параметрами, геометрические задачи, т.е. эти темы считаются трудными и в школьных учебниках очень мало рассматриваются.

Тематическое планирование:
Выражения и преобразования
корень n-й степени
степень с рациональным показателем
логарифм
синус, косинус, тангенс, котангенс
прогрессии
Уравнения и неравенства
уравнения с одной переменной
равносильность уравнений
общие приемы решения уравнений
системы уравнений с двумя переменными
неравенства с одной переменной
Демонстрационный тест ЕГЭ
Функции
числовые функции и их свойства
производная функции
исследование функции с помощью производной
первообразная
Числа и вычисления
проценты
пропорции
решение текстовых задач
Модули
Параметры
Геометрические фигуры и их свойства.
Измерение геометрических величин.
Пробный тест ЕГЭ

Выражения и преобразования
Выбор рационального пути во многом зависит от владения всем объемом информации о способах преобразований выражений. Задания для ЕГЭ составляются в расчете на ограниченное число формул, которые Вы можете вполне прочно усвоить, что позволит успешно выполнить предлагаемые задания.
Часть А. Задания с выбором ответа.
Вычислите:
16 ; 2) 2; 3) 0,5; 4) 3.
Решение:

Часть С. Задания с развернутым ответом
Найдите наибольшее значение параметра a, при котором уравнение x3+5x2+ax+b=0 c целыми коэффициентами имеет три различных корня, один из которых равен -2.
Решение. Подставив x=2 в левую часть уравнения, получим -8+20-2a+b=0, а значит, b=2a-12. Так как число - 2 является корнем, то можно вынести общий множитель x+2: x3+5x2+ax+b=x3+2x2+3x2+ax+(2а-12)= =x2(x+2)+3x(x+2)-6x+ax+(2a-12)=x2(x+2)+3x(x+2)+(a-6)(x+2)=(x+2)(x2+ +3x+(a-6)). По условию имеются еще два корня уравнения. Значит, дискриминант второго множителя положителен. D=(-3)2-4(a-6)=33-4a>0, т.е. a<8,25. Казалось бы, что ответом будет a=8. Но при подстановке числа 8 в исходное уравнение получаем: x3+5x2+ax+b= =x3+5x2+8x+4=(x+2)(x2+3x+2)=(x+1)(x+2)2, т.е. уравнение имеет только два различных корня. А вот при a=7 действительно получается три различных корня.
Ответ: 7.

Методика работы с модулями. Уравнения и неравенства. Системы
Прежде всего повторить понятие модуля на простейших примерах. Запомнить: модуль - это расстояние.
IХI=7,
а, если а >0,
Итак, IaI = 0, если а =0,
-а, если а<0
Свойства модуля действительного числа:
1. Iа + bI ≤ IаI + IbI ; 3. I1/aI=1/IaI ;
2. Iа bI = IаI IbI ; 4. Iа - bI ≥ IIаI – IbII .

1. Простейшие уравнения и неравенства.
I3х +1I=7; I1-2хI=43; I7-3хI=11; I2х-7I≤2; I18-xI≥48; I1+5xI<4;
I2-9xI>13.
2. Задания из ЕГЭ.
2.1 Пусть (x0y0)- решение системы x-1 – y=0,
y-Ix-5I=2.
Найти разность x 0–y0 (Задание В)
2.2 Найти наибольшее натуральное значение параметра с, при котором решение неравенства II2х+4I-7I-13≤2c2 удовлетворяет
условию х ∈ [-37; 35] (Задание С)
Решение:
1.1 I3х+1I=7; 3х+1=7 или 3х+1= -7; х=2 или х= -8/3
I1-2xI=43; 1-2x=43 или 1-2х= -43; x= - 21 или х= 22.
1.2 I2x-7I≤2 ; рис 1.
-2≤2x-7≤2;
2,5≤x≤4,5 Ответ [2,5; 4,5]
I8-xI≥48; 18 -x≥48 или 18-х≤-48, х≤-30 или х≥66
Ответ (-∞; -30] ∪ [66;∞).
I1+5xI<4; Используем рис. 1: -4<1+5x<4; -1
I2-9xI>13; Используем рис. 2: 2-9x>13 или 2-9x<-13;
Ответ (-∞; -11/9) ∪ (5/3;∞).

2.1 Для решения системы выразим одну переменную через другую
и применим метод интервалов.
1) x∈(-∞;5); x - 1 - (5-x)=2; x1=5; x2=10; оба корня не входят в заданный промежуток.
2) x∈[5; ∞); x - 1 - x+5=2; x1=2; x2=5; 2∈[5; ∞); 5 x∈[5; ∞)
y=2; x - y=3. Ответ: 3
2.2 II2x+4I-7I-13≤2c2;
по определению модуля - 2с2-13≤I2x+4I-7≤2c2+13; рассмотрим 2 варианта:
1)I2x+4I≤2c2+20; 2)I2x+4I≥-2c2-6 верно при любых с.
1)-2c2-2y≤2x≤2c2+16; -с2-12≤x≤c2+8; по условию x∈[-37;35], очевидно, что
с2+8=35, с2=27, с=5 - единственно возможное
-с2-12=-37; с2=25. натуральное значение с. Ответ: с=5

Геометрические фигуры и их свойства.
Измерение геометрических величин
Признаки равенства и подобия треугольников. Решение треугольников. Площадь треугольника.
Многоугольники.
Окружность.
Многогранники.
Тела вращения.
Комбинации тел.

Геометрические задачи относятся к группам B и С. Это вполне закономерно, поскольку чаще всего они требуют нестандартного подхода. Они меньше, чем алгебраические задачи, связаны с традиционными алгоритмами и приёмами.
Ученик, приступающий к решению, должен хорошо знать и уметь применять соответствующие определения и свойства геометрических фигур. Кроме того, в ходе анализа задачи важно точно устанавливать связи между элементами условия, правильно передавать это на геометрическом чертеже. Хорошо сделанный чертёж – половина решения задачи.
Упражнения, представленные в этом блоке, охватывают разные темы курса геометрии и включают в себя два раздела: «Задания по планиметрии» и «Задания по стереометрии».
Геометрические фигуры и их свойства.
Измерение геометрических величин

Задача 1 Три окружности радиуса 2 см попарно касаются друг друга. Найдите площадь фигуры ABC, заключённой между дугами окружности.
Решение:
соединим отрезками точки О1,О2,О3 – центры заданных окружностей. Площадь искомой фигуры есть разность площадей
SΔО1О2О3 - 3SCЕКТОРА.
SΔО1О2О3=a2 √3 /4, где а – сторона треугольника О1О2О3
SΔО1О2О3=4√ 3; SCЕКТОРА= πR2n/3600=
= π *4*600/3600 = 2π/3,
SФИГУРЫ =4 √ 3 - 3* 2π/3= (√ 3 - 2π) (см2)
Ответ: (√ 3 - 2π)

Задача 2 Длины окружностей оснований усечённого конуса равны 48π см и 16π см. Найдите поверхность сферы, вписанной в усечённый конус, если площадь его боковой поверхности равна сумме площадей оснований.
Решение:
Обозначим радиусы оснований R1=O1D и
R2 =O2С. По условию 48π = 2πR1; R1=24;
16π = 2πR2; R2=8.
SБОК.КОН.= πl(R1+R1), где R1, R1 –радиусы оснований,
l – образующая конуса.
Так как SБОК.КОН.= S1+S2, где S1, S2 – площади оснований
конуса, то πl(24+8)=π*242+ π*64. Отсюда
πl*32=640π, l=20 (см).
MD=O1D-O2С=24-8=16 (cм). СМ=O1O2, где O1O2 –
диаметр вписанной сферы. Из треугольника CMD
получаем: СМ=√СD2-MD2 =√400-256 =12 (см).
Отсюда RСФ.=6.
SСФ =4πR2=4π*36=144π(см2).
Ответ: 144 π.

Итоги ЕГЭ 2004-2005 уч.г.
выпускников лингвистической гимназии №3.
Учитель: Баханова Л.И.
по первичной шкале (0-37).

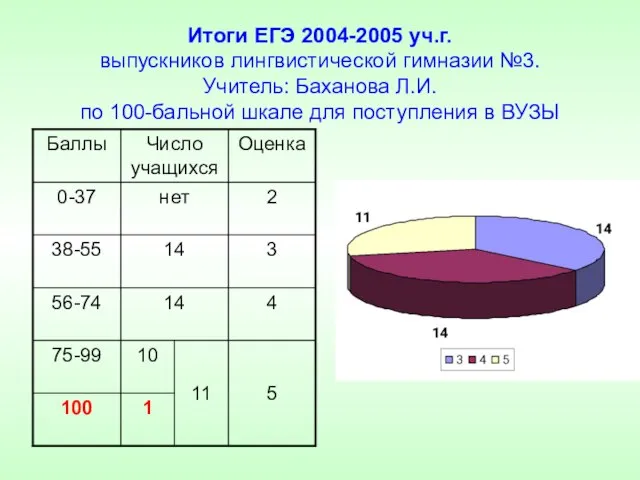
Итоги ЕГЭ 2004-2005 уч.г.
выпускников лингвистической гимназии №3.
Учитель: Баханова Л.И.
по 100-бальной шкале для поступления в ВУЗЫ

Итоги ЕГЭ 2004-2005 уч.г.
выпускников Кяхтинской СОШ №2.
Учитель: Булыгина Т.Г. По первичной шкале (0-37).

Литература:
Журнал «Математика в школе» 2002-05 г.
Газета «Математика»
Л.Д.Лаппо и др. Математика. ЕГЭ.
В.С.Туманов. Математика. ЕГЭ.
В.Н.Студенецкая. Математика. Система подготовки к ЕГЭ.
Т.А.Корешкова и др.Математика. ЕГЭ. Тестовые задания. Тренировочные задания.
А.Н.Рурукин. Математика. ЕГЭ.
Б.В.Соболь и др. Пособие по подготовке к ЕГЭ по математике.
О.Черкасов. Математика. Интенсивный курс подготовки к экзамену по математике.
Л.О.Денищева и др. ЕГЭ-2005. Математика.
С.И.Колесникова. Интенсивный курс подготовки к ЕГЭ по математике. Домашний репетитор.
Кодификатор элементов содержания по математике.
Особенности проведения экзамена по математике в 2005 году.
Анализ результатов экзамена 2004 года и рекомендации выпускникам по подготовке к ЕГЭ – 2005.