Содержание
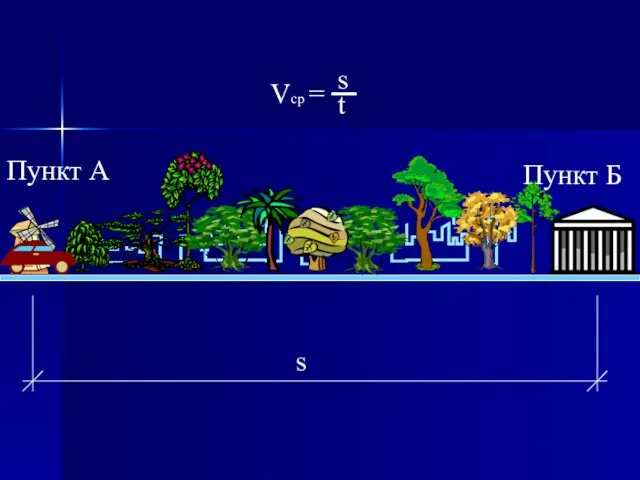
- 2. Пункт А Пункт Б s
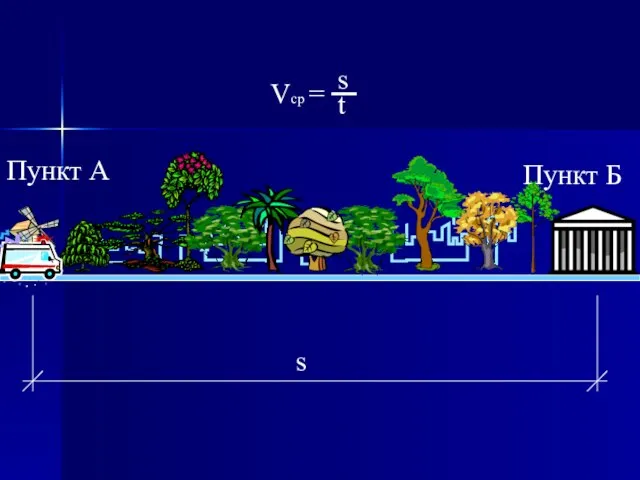
- 3. Пункт А Пункт Б s
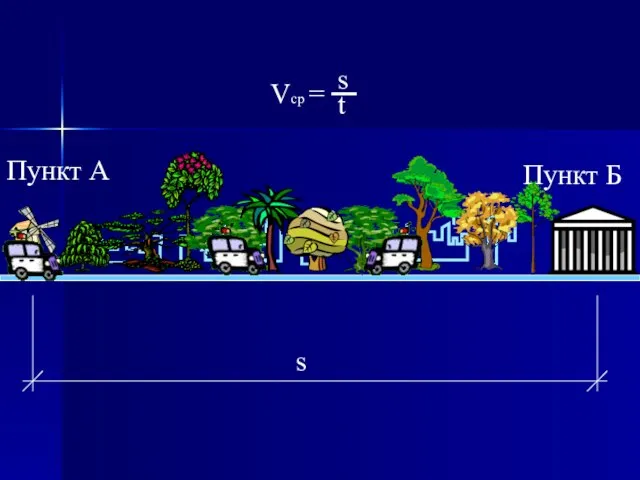
- 4. Пункт А Пункт Б s
- 5. Как видно, в этих трёх примерах расстояние между начальным и конечным пунктами фиксировано, время движения одинаково,
- 6. Очевидно, средняя скорость тем точнее харак-теризует существо вопроса, чем меньше про-межуток времени, на котором она измеряется.
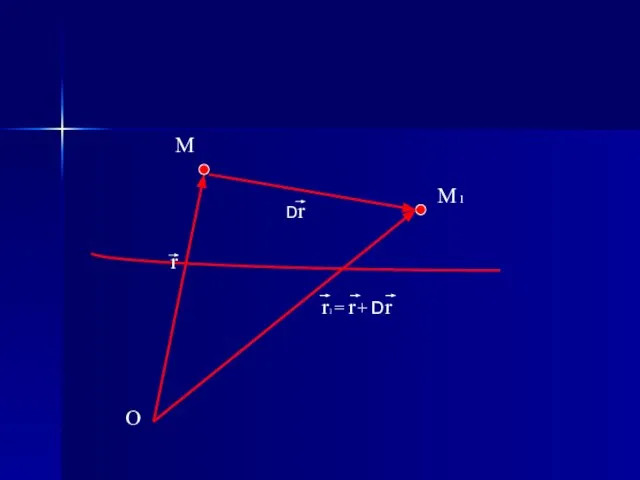
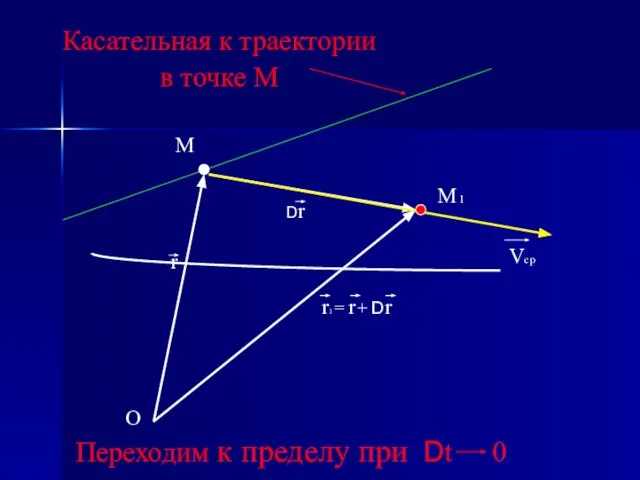
- 7. Пусть в момент времени t точка находится в положении М, которое задаётся радиусом-вектором r, а в
- 8. O r M M 1 Dr r1 = r + Dr
- 9. Dt O r M M 1 Dr r1 = r + Dr Dr Vcp = -
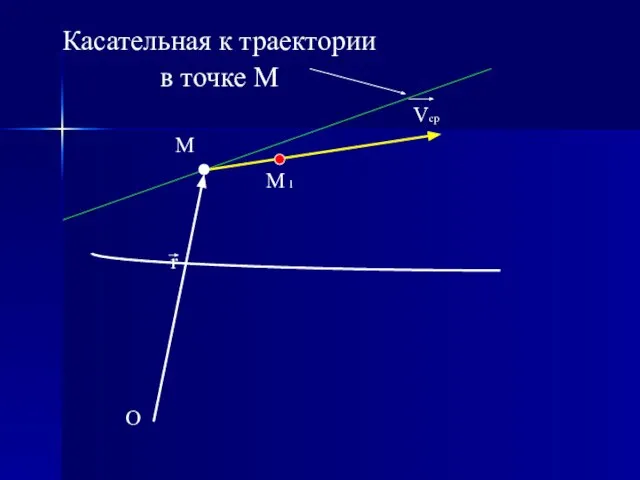
- 10. O r M M 1 Dr r1 = r + Dr Vcp Касательная к траектории в
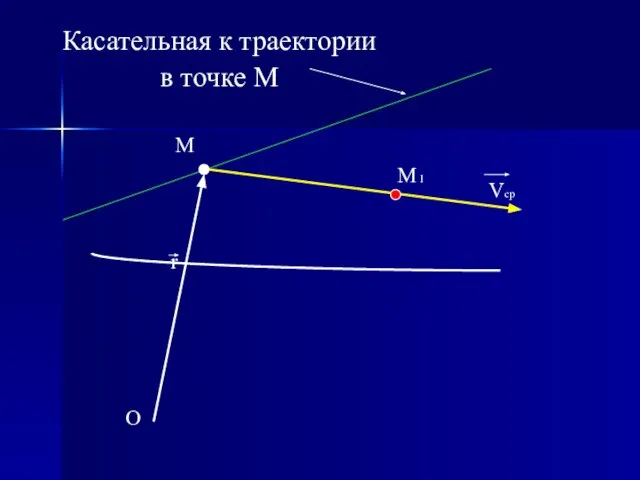
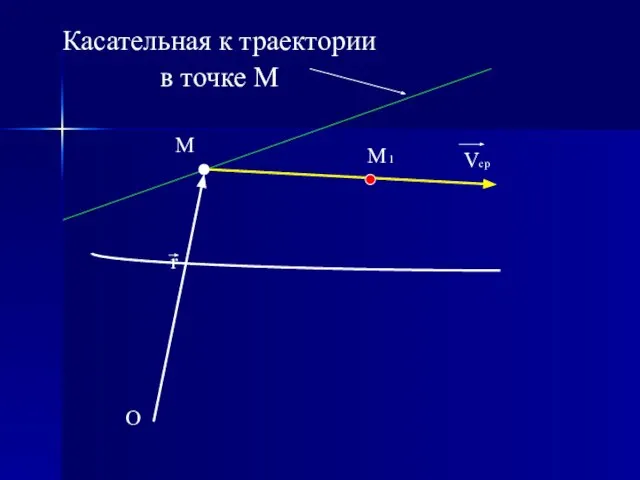
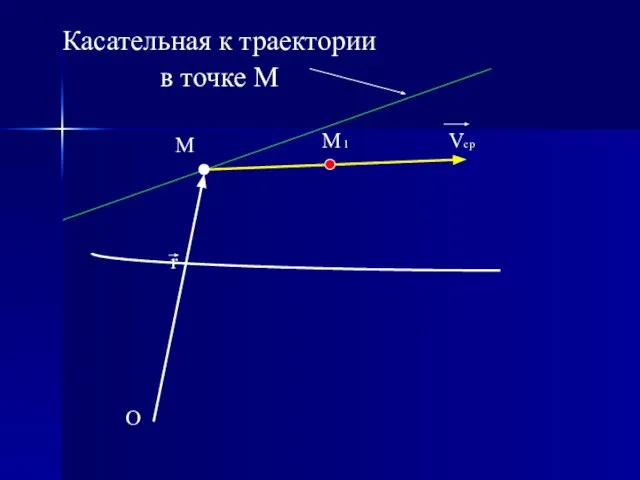
- 11. O r M M 1 Vcp Касательная к траектории в точке М
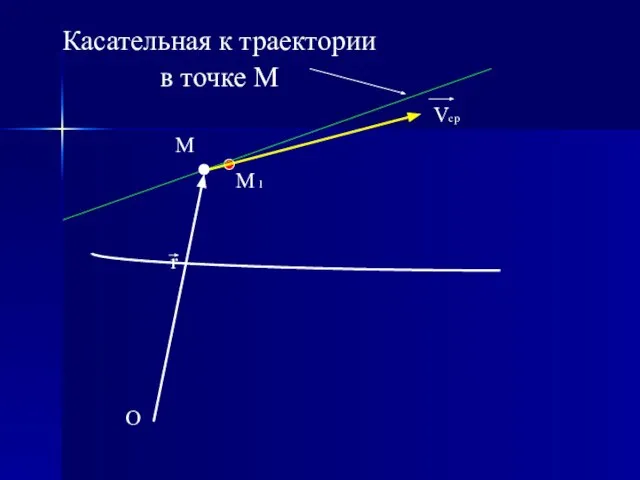
- 12. O r M M 1 Vcp Касательная к траектории в точке М
- 13. O r M M 1 Vcp Касательная к траектории в точке М
- 14. O r M M 1 Vcp Касательная к траектории в точке М
- 15. O r M M 1 Vcp Касательная к траектории в точке М
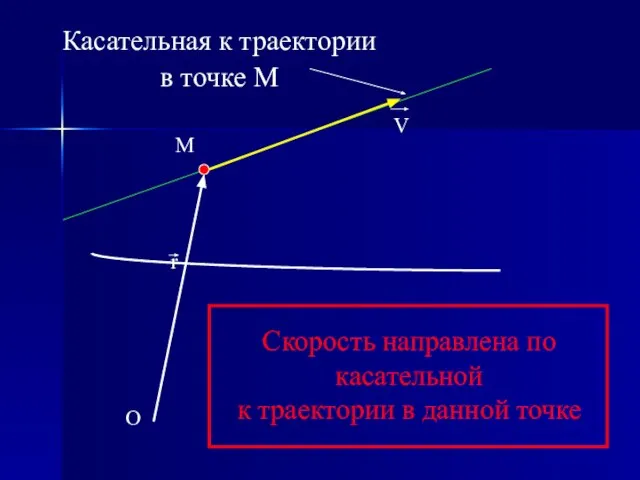
- 16. O r M V Скорость направлена по касательной к траектории в данной точке Касательная к траектории
- 17. Таким образом, скорость точки равна первой производной по времени от радиуса-вектора точки Учитывая, что единичные векторы
- 19. Скачать презентацию





 Парциальная программа Л.Л. Тимофеевой Формирование культуры безопасности
Парциальная программа Л.Л. Тимофеевой Формирование культуры безопасности Семинар 3. Знакомство с языками программирования
Семинар 3. Знакомство с языками программирования Происхождение денег
Происхождение денег Медицинский симпозиум
Медицинский симпозиум Военно-полевые сборы.
Военно-полевые сборы. Русский терем
Русский терем Вышивка
Вышивка Иван Иванович Шишкин - живописец и гравер, мастер пейзажа
Иван Иванович Шишкин - живописец и гравер, мастер пейзажа Тема 1. Функциональные возможности ГИС Занятие № 2. Ввод, предоб-работка и хранение данных
Тема 1. Функциональные возможности ГИС Занятие № 2. Ввод, предоб-работка и хранение данных Презентация на тему Классификация Компьютерных сетей
Презентация на тему Классификация Компьютерных сетей  Не с причастиями
Не с причастиями Презентация по теме: «Формирование экологических представлений у детей младшего дошкольного возраста»
Презентация по теме: «Формирование экологических представлений у детей младшего дошкольного возраста» АВАРИИ НА ХОО и РОО (химически опасных объектах) (радиационно опасных объектах)
АВАРИИ НА ХОО и РОО (химически опасных объектах) (радиационно опасных объектах) Изготовление оберега «Кукла-закрутка»
Изготовление оберега «Кукла-закрутка» Презентация на тему Проецирование. Виды проецирования
Презентация на тему Проецирование. Виды проецирования Антропогенная нагрузка и устойчивость ландшафта
Антропогенная нагрузка и устойчивость ландшафта Украинский фондовый рынок с точки зрения технического анализа – настоящее и перспективы
Украинский фондовый рынок с точки зрения технического анализа – настоящее и перспективы Культура эпохи Возрождения
Культура эпохи Возрождения Роль России и ЕС в конфликтах и кризисах на постсоветском пространстве
Роль России и ЕС в конфликтах и кризисах на постсоветском пространстве амортиз пр
амортиз пр Учим состав числа от 5 до 10
Учим состав числа от 5 до 10 Права студентов
Права студентов Предложение по размещению рекламы в салонах красоты
Предложение по размещению рекламы в салонах красоты Политическое развитие
Политическое развитие Использование ИКТ как способ формирования ключевых компетенций учащихся.Выполнила Ровенских С.В., учитель английского языка МОУ
Использование ИКТ как способ формирования ключевых компетенций учащихся.Выполнила Ровенских С.В., учитель английского языка МОУ  Проблеми зняття з експлуатації об’єктів ядерної енергетики та відновлення навколишнього середовища
Проблеми зняття з експлуатації об’єктів ядерної енергетики та відновлення навколишнього середовища Побег. Строение и значение побега
Побег. Строение и значение побега Почему мы спим ночью? (1 класс)
Почему мы спим ночью? (1 класс)