Содержание
- 2. План доклада 1. Происхождение социофизики и области ее интересов 2. Проявления физических факторов в социуме 3.
- 3. Социальная система: совокупность N (>>1) взаимодействующих индивидов во внешней среде. Экономика, политика, экология и т.д. =
- 4. «Частица материи не может сказать нам, что она вовсе не чувствует потребности притягивания и отталкивания и
- 5. Происхождение социофизики 1. Теоретические модели (гидродинамика, неравновесная термодинамика, теория фазовых переходов, кинетика) и сложные физические системы
- 6. Стенли Г. Фазовые переходы и критические явления (пер. с англ.) – М.: Мир, 1973. Хакен Г.
- 7. Каналы влияния физических факторов на социальные системы 1. Диссипативный характер глобальной подсистемы “человечество на Земле в
- 8. Основные направления социофизики 1. Коллективное движение в социальных системах: машины и пешеходы (1D), crowd control (2D),
- 9. S.Galam Sociophysics: a physicist’s modeling of psycho-political phenomena. 2012, Springer, 536 p. B.K.Chakrabarti, A.Chakraborti, A Chatterjee
- 10. Dirk Helbing. Quantitative Sociodynamics: Stochastic Methods and Models of Social Interaction Processes, 2nd Edition, Springer, 2010
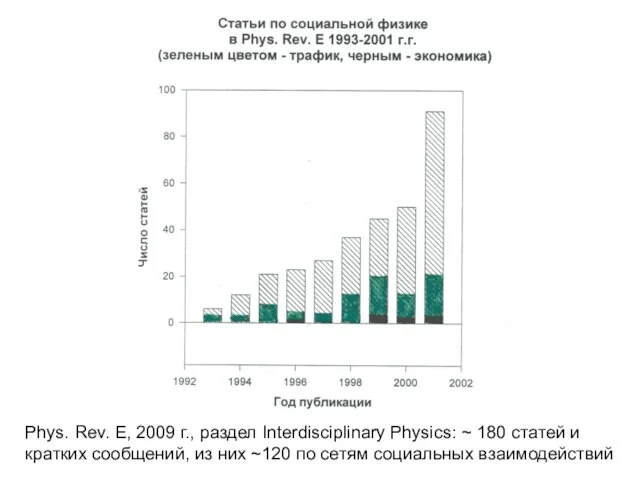
- 11. Phys. Rev. E, 2009 г., раздел Interdisciplinary Physics: ~ 180 статей и кратких сообщений, из них
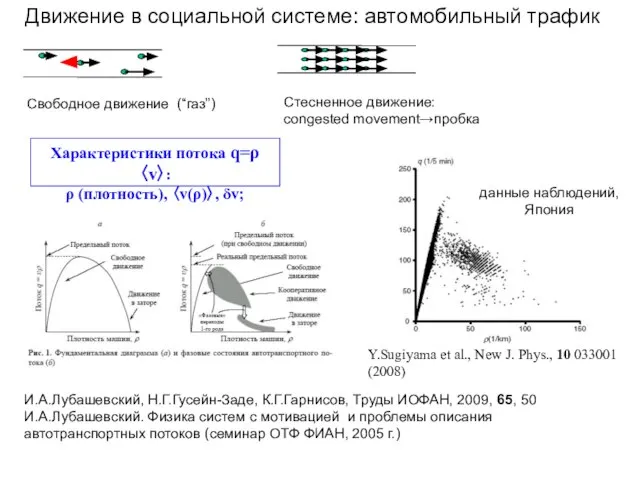
- 12. Движение в социальной системе: автомобильный трафик Свободное движение (“газ”) Стесненное движение: congested movement→пробка Характеристики потока q=ρ〈v〉:
- 13. Особенности движения в системе «живых частиц» θi(t+1) = 〈 θj(t)〉окружение + η где θi – направление
- 14. C.W. Reynolds, Computer Graphics, 21(4) 25-34 (1987)
- 15. midvi/dt = Fiинд + Fiобщ + ηi(t) Fiинд = (mi/τ)(vi(0)e – vi) Fiобщ. = −∑цели fik
- 16. T.Vicsek. Crowd control: a physicist’s approach to collective human behaviour. EPS-12 (European Physical Society), Budapest 2002
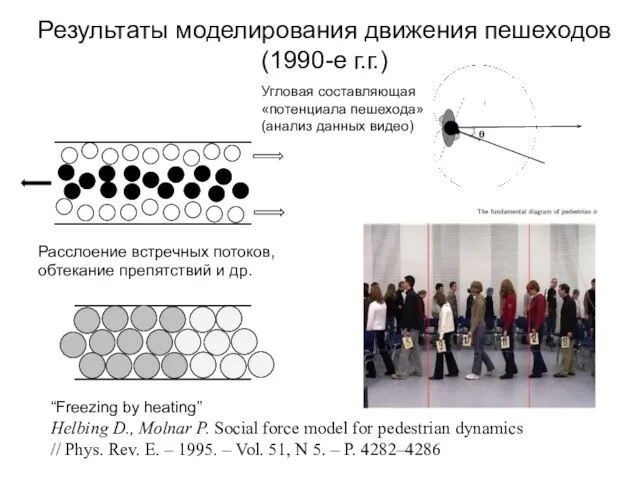
- 17. “Freezing by heating” Helbing D., Molnar P. Social force model for pedestrian dynamics // Phys. Rev.
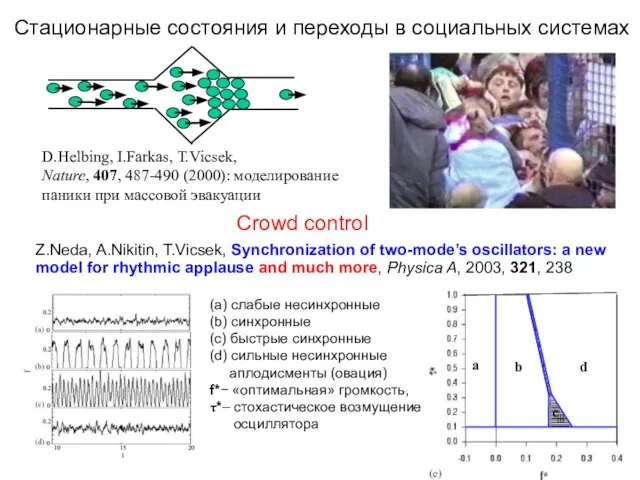
- 18. Crowd control Стационарные состояния и переходы в социальных системах Z.Neda, A.Nikitin, T.Vicsek, Synchronization of two-mode’s oscillators:
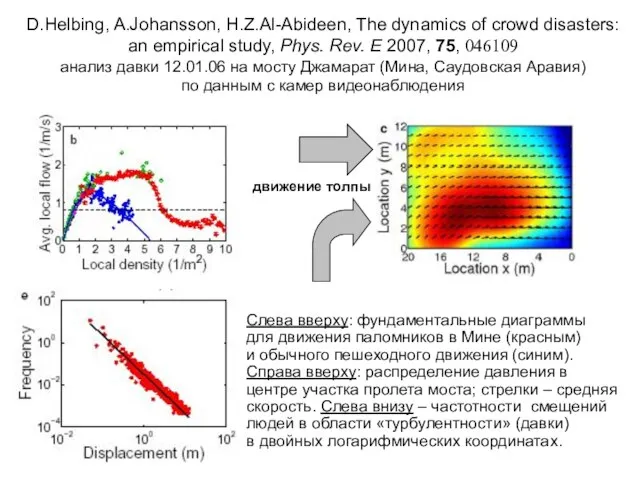
- 19. D.Helbing, A.Johansson, H.Z.Al-Abideen, The dynamics of crowd disasters: an empirical study, Phys. Rev. E 2007, 75,
- 20. J.R.G. Dyer, et al., Leadership, consensus decision making and collective behaviour in humans. Phil. Trans. Royal
- 21. Сети социальных взаимодействий (выборочно) Монографии и учебники: 1. M.Newman, A.-L.Barabasi, D.J.Watts (Eds.), The Structure and Dynamics
- 22. Д.А. Губанов, Д.А. Новиков, А.Г. Чхартишвили. Социальные сети: модели информационного влияния, управления и противоборства «Онлайновые социальные
- 23. Фрагменты сложных сетей (complex networks) регулярный граф полный граф реализация случайного графа, полученного преобразованием регулярного графа:
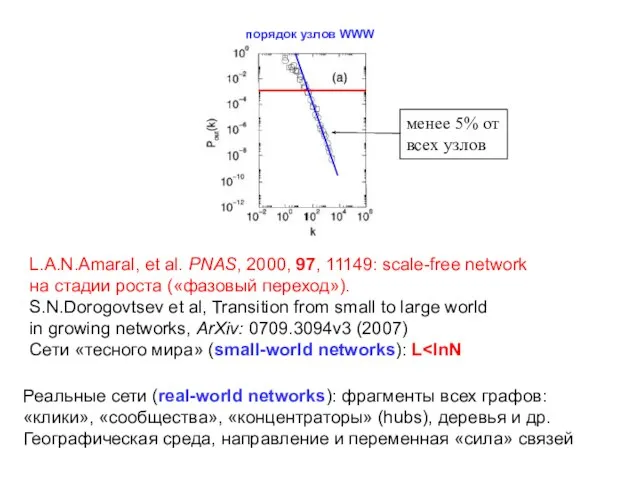
- 24. L.A.N.Amaral, et al. PNAS, 2000, 97, 11149: scale-free network на стадии роста («фазовый переход»). S.N.Dorogovtsev et
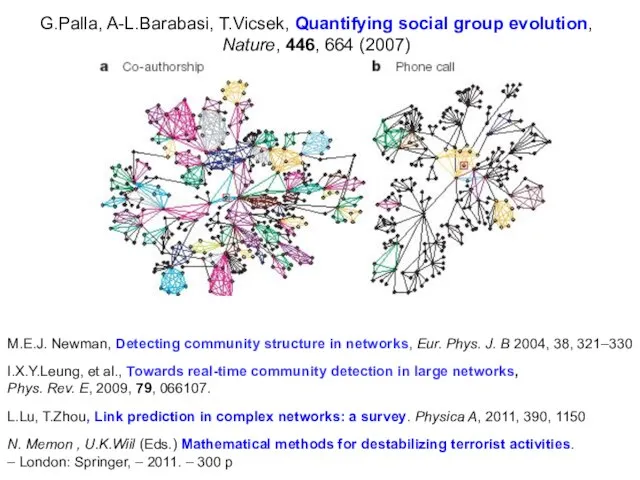
- 25. G.Palla, A-L.Barabasi, T.Vicsek, Quantifying social group evolution, Nature, 446, 664 (2007) M.E.J. Newman, Detecting community structure
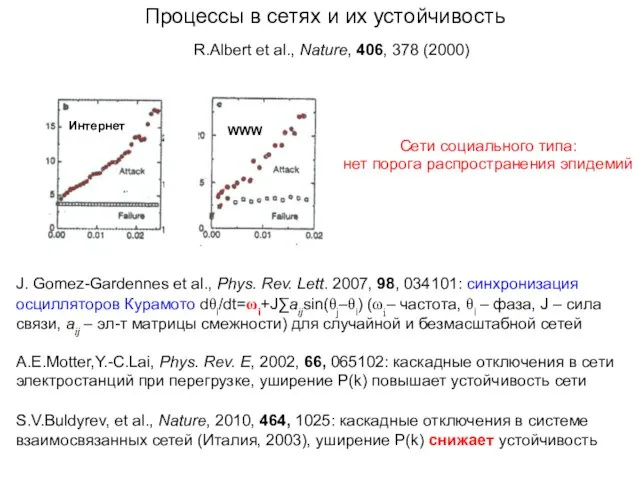
- 26. Процессы в сетях и их устойчивость R.Albert et al., Nature, 406, 378 (2000) Сети социального типа:
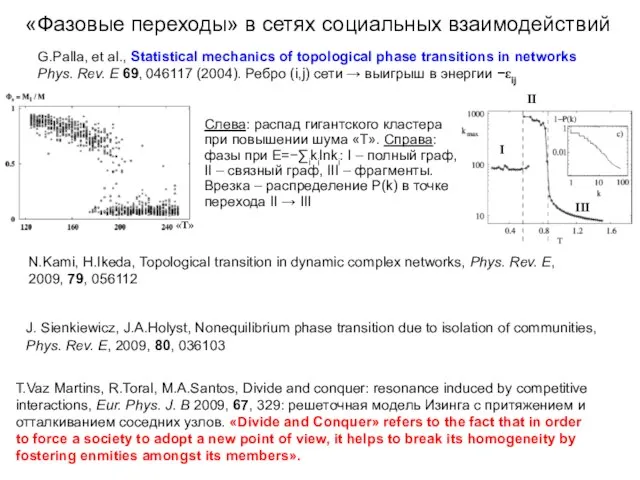
- 27. G.Palla, et al., Statistical mechanics of topological phase transitions in networks Phys. Rev. E 69, 046117
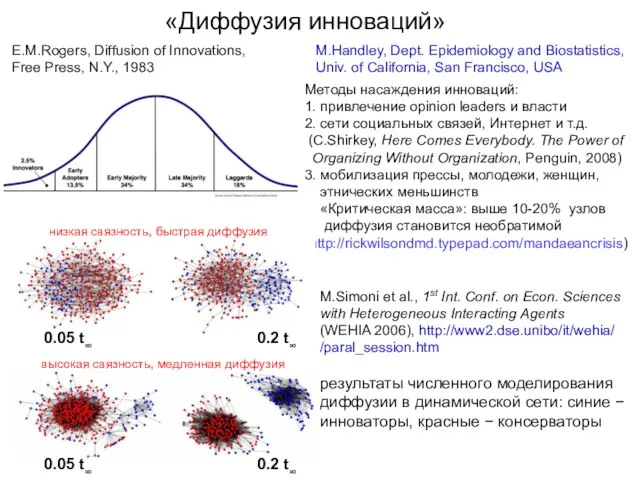
- 28. «Диффузия инноваций» M.Handley, Dept. Epidemiology and Biostatistics, Univ. of California, San Francisco, USA Методы насаждения инноваций:
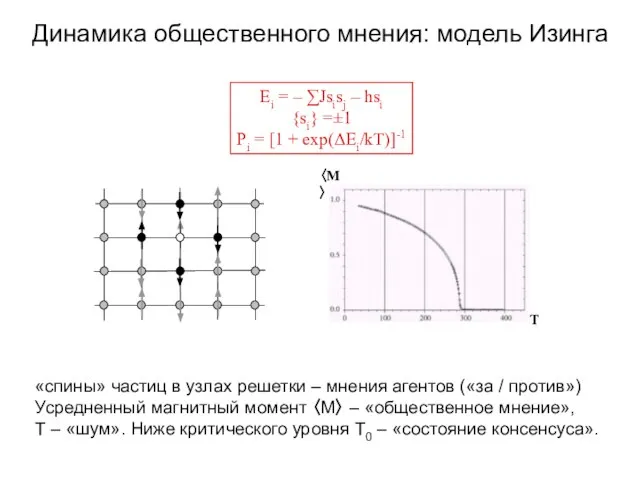
- 29. Динамика общественного мнения: модель Изинга Ei = – ∑Jsisj – hsi {si} =±1 Pi = [1
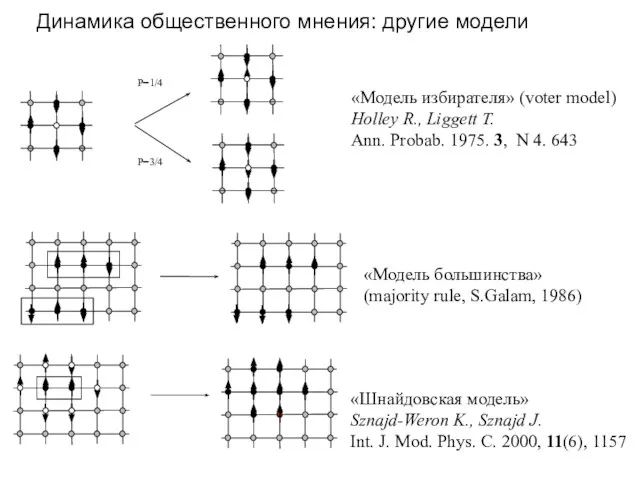
- 30. Динамика общественного мнения: другие модели «Модель большинства» (majority rule, S.Galam, 1986) P=1/4 P=3/4 «Модель избирателя» (voter
- 31. В основе всех моделей – случайное изменение мнения агента под воздействием окружения. В моделях обычно побеждает
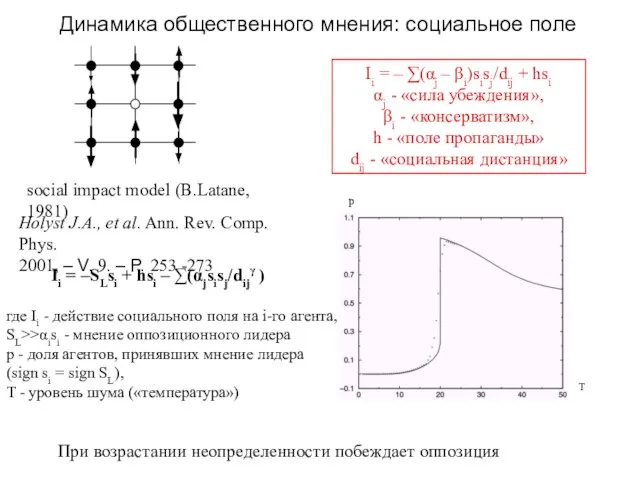
- 32. Динамика общественного мнения: социальное поле Ii = – ∑(αj – βi)sisj/dij + hsi αj - «сила
- 33. Непрерывная переменная мнения: модель де Гроота Модель де Гроота: n агентов с мнениями s(t)=(x1(t), x2(t), …,
- 34. Расчетные модели с непрерывным мнением {xi(t)∈[0,1]} «Условное доверие» (bounded confidence): вычисляется Δxij(t)=xi(t)–xj(t), и если 0 M.Afshar,
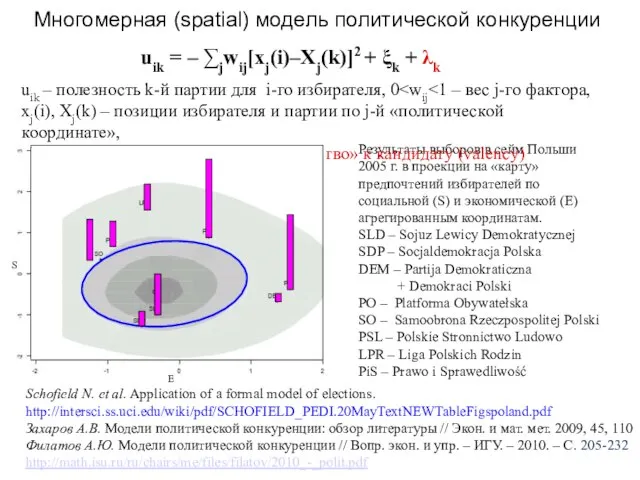
- 35. Многомерная (spatial) модель политической конкуренции Schofield N. et al. Application of a formal model of elections.
- 36. Модели политического кризиса Пороговые модели (threshold models): переход агента f1(t)→f2(t+1) при критическом значении параметра его окружения
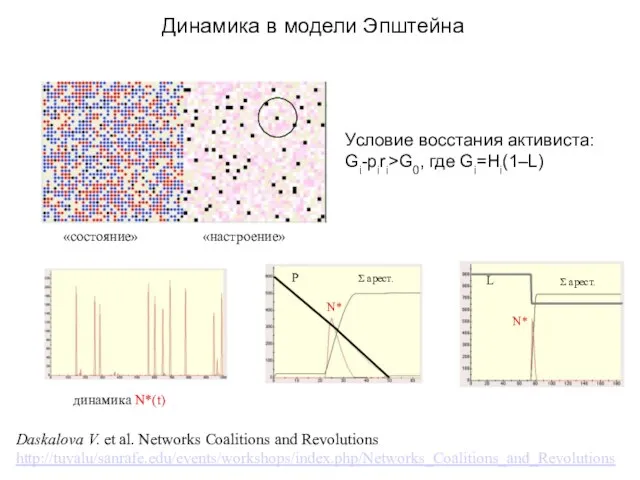
- 37. Daskalova V. et al. Networks Coalitions and Revolutions http://tuvalu/sanrafe.edu/events/workshops/index.php/Networks_Coalitions_and_Revolutions Динамика в модели Эпштейна Условие восстания активиста:
- 38. Моделирование гражданских войн 1. M.G.Findley, Agents and conflict: adaptation and the dynamics of war, Complexity, 2008,
- 39. «Self-organized criticality» Стратегия «управляемого хаоса»: Mann S.R. Chaos theory and strategic thought, // Parameters (US Army
- 40. Примеры исследований; по теме «twitter»: Gonzalez-Bailon S., et al. The dynamics of protest recruitment through an
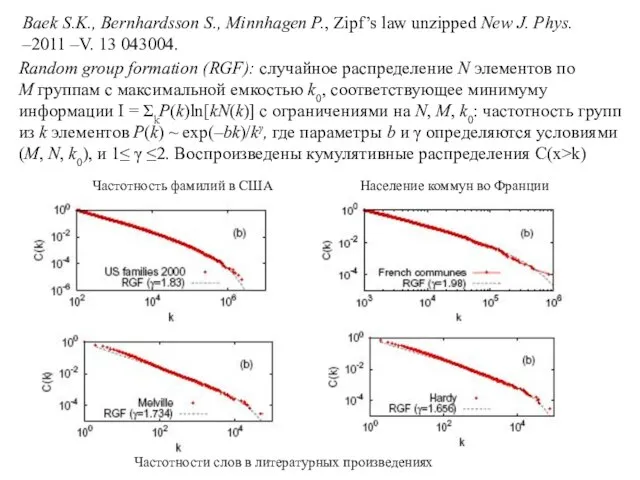
- 41. Baek S.K., Bernhardsson S., Minnhagen P., Zipf’s law unzipped New J. Phys. –2011 –V. 13 043004.
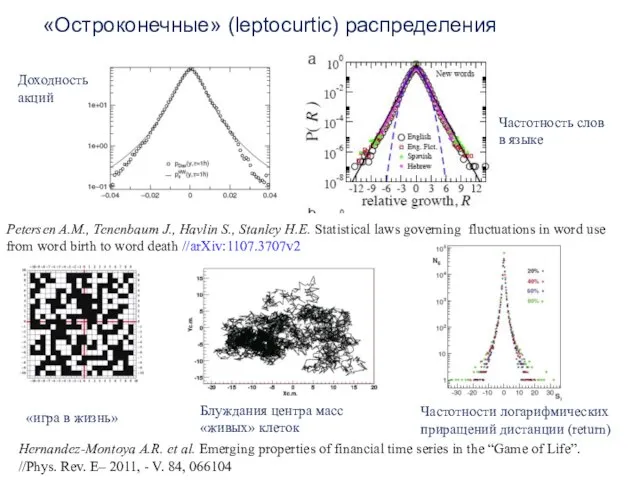
- 42. Petersen A.M., Tenenbaum J., Havlin S., Stanley H.E. Statistical laws governing fluctuations in word use from
- 43. Выводы 1. Физическое описание и моделирование социальных явлений - новая, быстро растущая область естествознания (социофизика): встречное
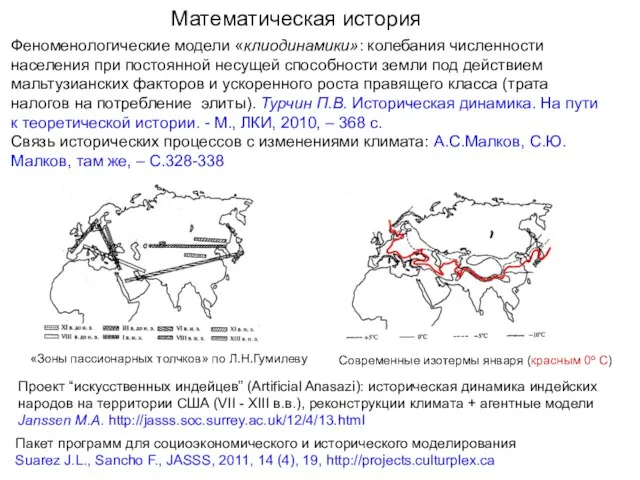
- 44. Математическая история Пакет программ для социоэкономического и исторического моделирования Suarez J.L., Sancho F., JASSS, 2011, 14
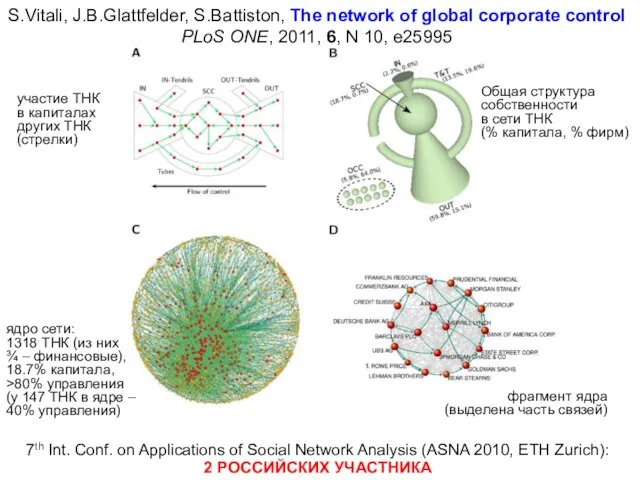
- 45. S.Vitali, J.B.Glattfelder, S.Battiston, The network of global corporate control PLoS ONE, 2011, 6, N 10, e25995
- 47. Скачать презентацию



















![Расчетные модели с непрерывным мнением {xi(t)∈[0,1]} «Условное доверие» (bounded confidence): вычисляется Δxij(t)=xi(t)–xj(t),](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/461470/slide-33.jpg)





 Тема: «Спортивные игры зимой»
Тема: «Спортивные игры зимой» Список детей на получение кроватей и полотенец
Список детей на получение кроватей и полотенец Тепловые двигатели. Паровая турбина.
Тепловые двигатели. Паровая турбина. Система образования в Англии
Система образования в Англии Геометрические паркеты
Геометрические паркеты Подходы к системному целеполаганию. Лекция 2
Подходы к системному целеполаганию. Лекция 2 Конституция РФ
Конституция РФ Проект "Задачи на смеси и сплавы"
Проект "Задачи на смеси и сплавы" Раздел #. Дизайн интерьера
Раздел #. Дизайн интерьера Основы научных исследований
Основы научных исследований 000834aa-f5be4922
000834aa-f5be4922 Погружение
Погружение Невербальное общение
Невербальное общение Однородность керамзита
Однородность керамзита Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения Презентация на тему Экономика как наука
Презентация на тему Экономика как наука Кофемашина Yamaguchi CoffeeMann
Кофемашина Yamaguchi CoffeeMann Танковая викторина
Танковая викторина Петр Петрович Семёнов-Тян-Шанский
Петр Петрович Семёнов-Тян-Шанский Александр
Александр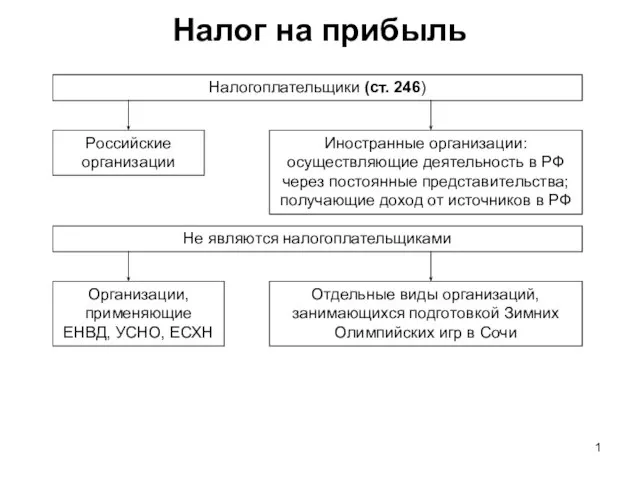 Налог на прибыль
Налог на прибыль SPORTS in Our Life
SPORTS in Our Life  Аудирование —цель и средство обучения
Аудирование —цель и средство обучения Отношения мужчины и женщины. Женская психология
Отношения мужчины и женщины. Женская психология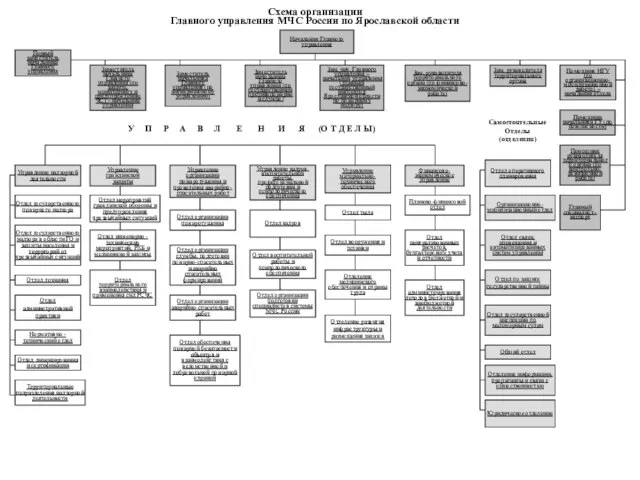 Схема организации Главного управления МЧС России по Ярославской области
Схема организации Главного управления МЧС России по Ярославской области Презентация на тему Афанасий Афанасьевич Фет (4 класс)
Презентация на тему Афанасий Афанасьевич Фет (4 класс) муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор
муниципальное образовательное учреждениеОбходская основная общеобразовательная школаУренского муниципального районаНижегор куликовская битва
куликовская битва