Содержание
- 2. Неупорядоченные сплавы Примесные атомы вместе с атомами кристалла (матрицы) образуют твердые растворы или сплавы. Различают два
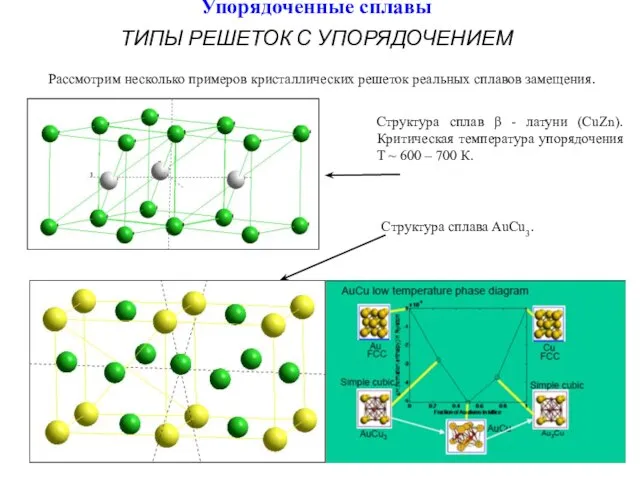
- 3. Упорядоченные сплавы ТИПЫ РЕШЕТОК С УПОРЯДОЧЕНИЕМ Структура сплав β - латуни (CuZn). Критическая температура упорядочения Т
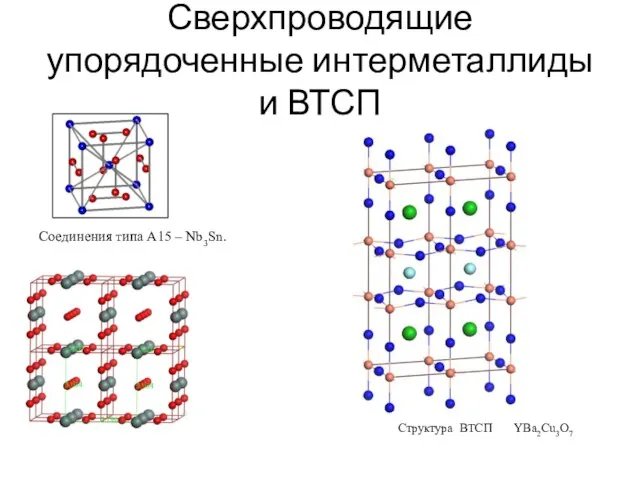
- 4. Сверхпроводящие упорядоченные интерметаллиды и ВТСП Соединения типа А15 – Nb3Sn. Структура ВТСП YBa2Cu3O7
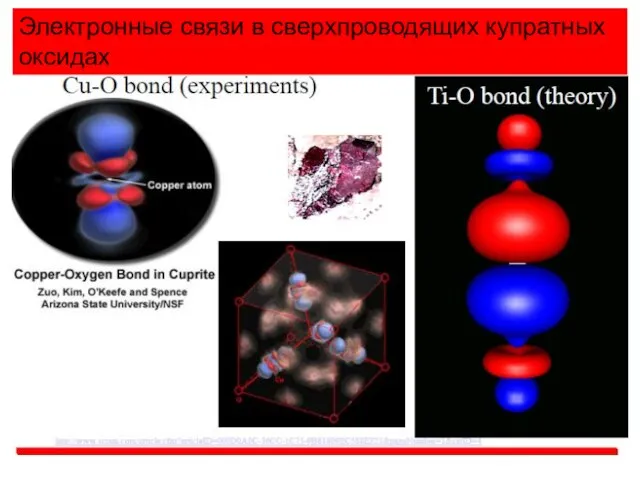
- 5. Электронные связи в сверхпроводящих купратных оксидах
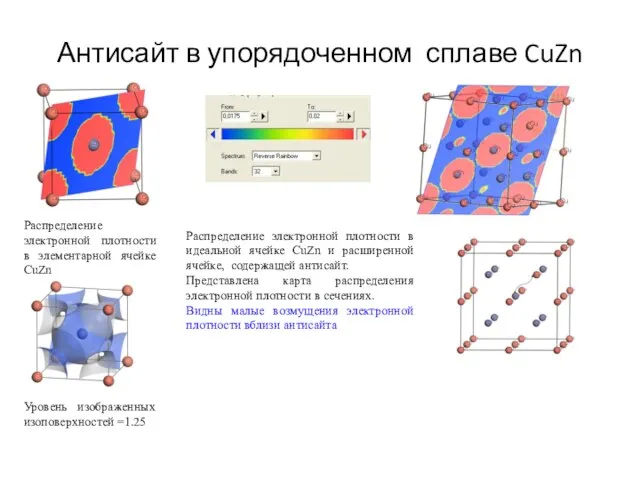
- 6. Антисайт в упорядоченном сплаве CuZn Распределение электронной плотности в идеальной ячейке CuZn и расширенной ячейке, содержащей
- 7. Сплавы замещения – Упорядочение в сплавах замещения тесно связано со стехиометрическим соотношением компонент. Только стехиометрический состав
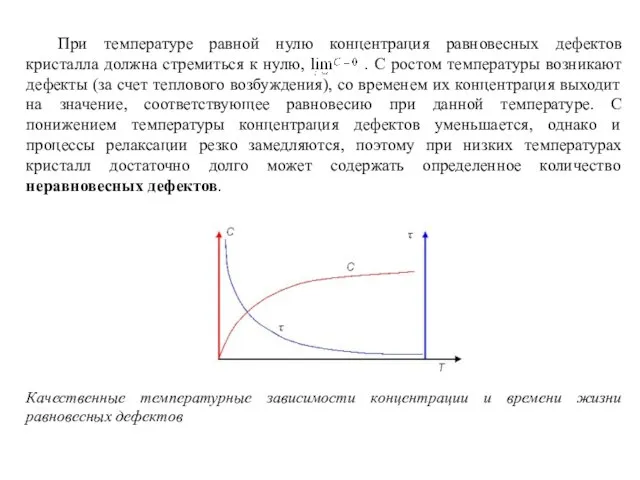
- 8. При температуре равной нулю концентрация равновесных дефектов кристалла должна стремиться к нулю, . С ростом температуры
- 9. Существует множество процессов, при которых возникают точечные дефекты. Большинству прямых процессов рождения можно сопоставить обратные процессы
- 10. В описанных выше механизмах рождения дефектов речь шла о термоактивированных процессах. Появляющиеся в этих процессах дефекты
- 11. Упорядочивающиеся сплавы В упорядочивающихся сплавах появляется новый тип дефектов – антисайт. В кристалле упорядочивающегося сплава из
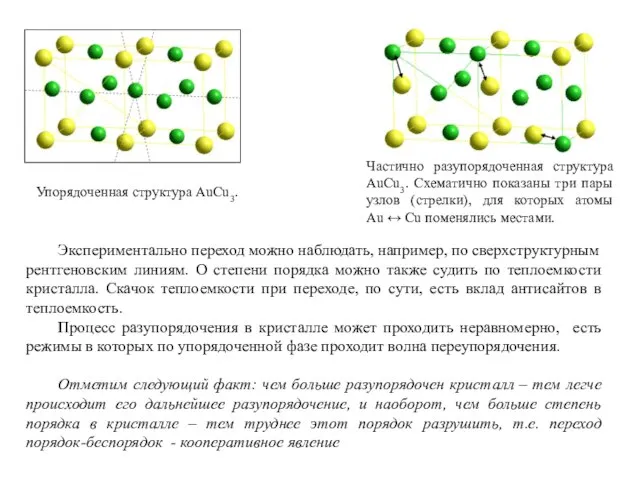
- 12. Частично разупорядоченная структура AuCu3. Схематично показаны три пары узлов (стрелки), для которых атомы Au ↔ Cu
- 13. ИТОГ:
- 15. Равновесная концентрация точечных дефектов в простых веществах Будем считать, что рассматриваемый кристалл представляет собой чистый металл.
- 16. Равновесная концентрация точечных дефектов в простых веществах Пренебрегаем эффектом изменения колебательной энтропии в связи с введение
- 17. ДЗ Задача 1 Ввести в задачу о равновесной конценрации дефектов давление. Подходящий потенциала -термодинамический потенциал ,
- 19. Скачать презентацию










 Островский на сцене театра
Островский на сцене театра Презентация
Презентация 20171221_stroenie_zemnoy_kory_k_konspektu
20171221_stroenie_zemnoy_kory_k_konspektu Сказать жизни Да
Сказать жизни Да Презентация на тему Мотивация персонала
Презентация на тему Мотивация персонала Политические режимы и государственная власть
Политические режимы и государственная власть Задачи по уголовному праву
Задачи по уголовному праву Сестринский процесс при болезнях почек
Сестринский процесс при болезнях почек Chill Map. Исследовательский проект
Chill Map. Исследовательский проект Состав комплекса. Роль транспорта
Состав комплекса. Роль транспорта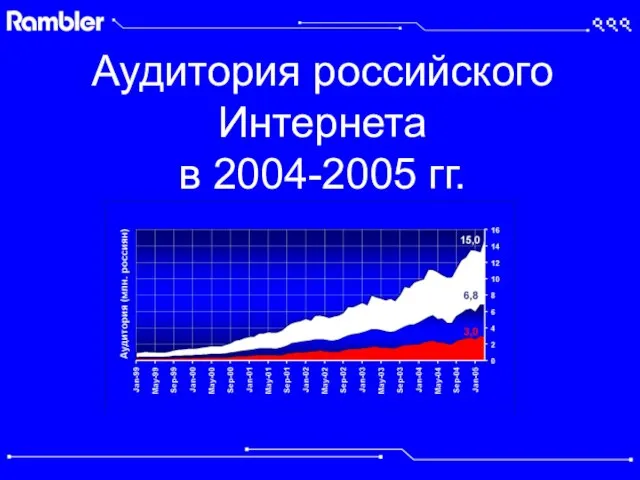 Аудитория российского Интернета в 2004-2005 гг.
Аудитория российского Интернета в 2004-2005 гг. Объекты для Субъектов МСП, включенные в перечень муниципального имущества г.о. Новокуйбышевск
Объекты для Субъектов МСП, включенные в перечень муниципального имущества г.о. Новокуйбышевск Сущность, функции и принципы управления образовательными системами
Сущность, функции и принципы управления образовательными системами Ты искал, ты искал, очень долго ты правду искал. Ты устал, не нашел, и надежду найти потерял. Открывал тайники, испытал и обиду, и ме
Ты искал, ты искал, очень долго ты правду искал. Ты устал, не нашел, и надежду найти потерял. Открывал тайники, испытал и обиду, и ме Применение ферромагнетиков
Применение ферромагнетиков kontrolnaya_rabota_10_kl
kontrolnaya_rabota_10_kl Химические формулы. Относительная атомная и относительная молекулярная массы
Химические формулы. Относительная атомная и относительная молекулярная массы История английского алфавита
История английского алфавита Презентация на тему Афины
Презентация на тему Афины  Наш Пермский край
Наш Пермский край Моделирование основных бизнес-процессов Jurby WaterTech International
Моделирование основных бизнес-процессов Jurby WaterTech International Исследование графиков функций Средствами программирования в QBasic
Исследование графиков функций Средствами программирования в QBasic Руку дружбы - хрустальному роднику!
Руку дружбы - хрустальному роднику! Тема 1.
Тема 1. WALTER PUT YOUR DICK AWAY
WALTER PUT YOUR DICK AWAY Шаблон ПРЕЗЕНТАЦИИ к рубежной аттестации 1 курс ОПД-1
Шаблон ПРЕЗЕНТАЦИИ к рубежной аттестации 1 курс ОПД-1 Карасёва Людмила АршавировнаЗинатулин Алексей МансуровичИННОВАЦИОННОЕ РАЗВИТИЕ ЭКОНОМИКИ: ПРОЕКТИРОВАНИЕ ИЗ БУДУЩЕГО?Кафед
Карасёва Людмила АршавировнаЗинатулин Алексей МансуровичИННОВАЦИОННОЕ РАЗВИТИЕ ЭКОНОМИКИ: ПРОЕКТИРОВАНИЕ ИЗ БУДУЩЕГО?Кафед Архитектура ЭВМ
Архитектура ЭВМ