Исследование графиков функций Средствами программирования в QBasic

Программа построения графика функции y=x
DECLARE FUNCTION f! (x!)
SCREEN 9
COLOR 1, 15
xmin = -320: xmax = 320
ymin = -175: ymax = 175
WINDOW (xmin, ymax)-(xmax, ymin)
LINE (xmin, 0)-(xmax, 0)
LINE (0, ymin)-(0, ymax)
LOCATE 2, 40: PRINT "y";
LOCATE 13, 75: PRINT "X";
LOCATE 2, 75: PRINT "I";
LOCATE 2, 2: PRINT "II";
LOCATE 22, 2: PRINT "III";
LOCATE 22, 75: PRINT "IV";
k = 10000
FOR x = xmin TO xmax STEP (xmax - xmin) / k
y = f(x)
CIRCLE (x, y), 2, 3
NEXT x
FUNCTION f (x)
f = x
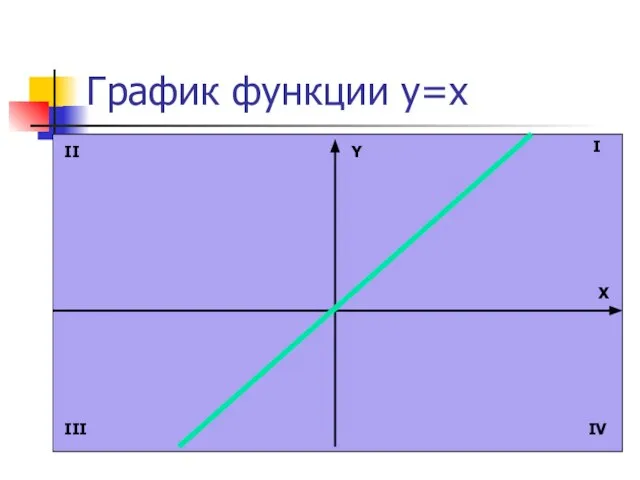
END FUNCTION

График функции y=x
Y
X
I
II
III
IV

Отрицательные и положительные значения функций
Положительные значения функции – это
Учитывая это, подправим программу с условием, что при положительных значениях функции график был
красного цвета,
а при отрицательных –
синего цвета.
Отрицательные значения функции – это
y<0
y>0

Отредактированный текст программы
DECLARE FUNCTION f! (x!)
SCREEN 9
COLOR 1, 15
xmin = -320: xmax = 320
ymin = -175: ymax = 175
WINDOW (xmin, ymax)-(xmax, ymin)
LINE (xmin, 0)-(xmax, 0)
LINE (0, ymin)-(0, ymax)
LOCATE 2, 40: PRINT "y";
LOCATE 13, 75: PRINT "X";
LOCATE 2, 75: PRINT "I";
LOCATE 2, 2: PRINT "II";
LOCATE 22, 2: PRINT "III";
LOCATE 22, 75: PRINT "IV";
k = 10000
FOR x = xmin TO xmax STEP (xmax - xmin) / k
y = f(x)
IF y > 0 THEN CIRCLE (x, y), 2, 4 ELSE CIRCLE (x, y), 2, 1
NEXT x
FUNCTION f (x)
f = ABS(x) - 50
END FUNCTION

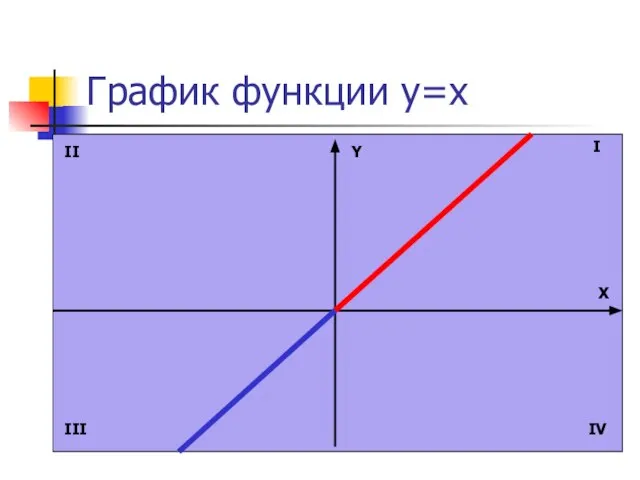
График функции y=x
Y
X
I
II
III
IV

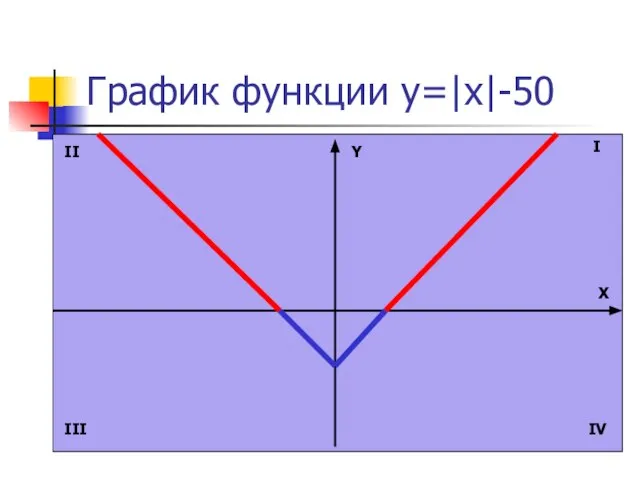
График функции y=|x|-50
Y
X
I
II
III
IV

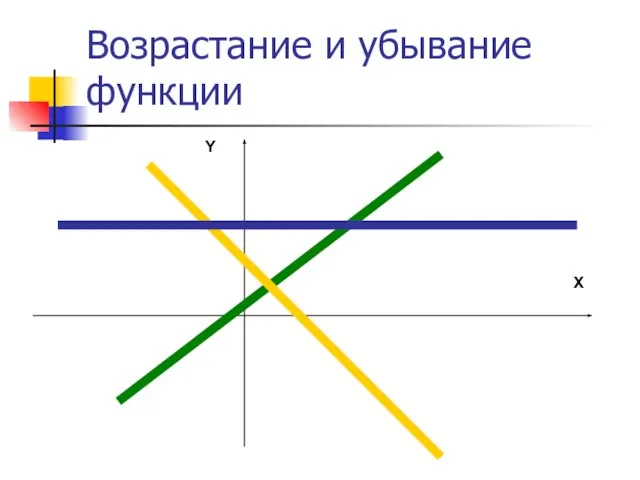
Возрастание и убывание функции
X
Y

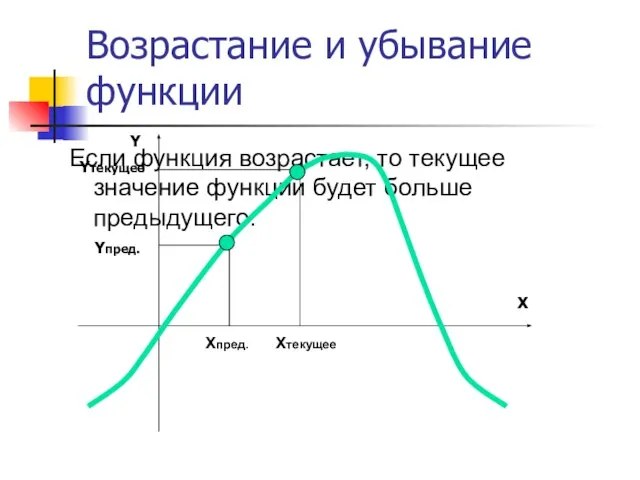
Возрастание и убывание функции
Если функция возрастает, то текущее значение функции будет больше предыдущего.
Yпред.
Yтекущее
Xпред.
Xтекущее

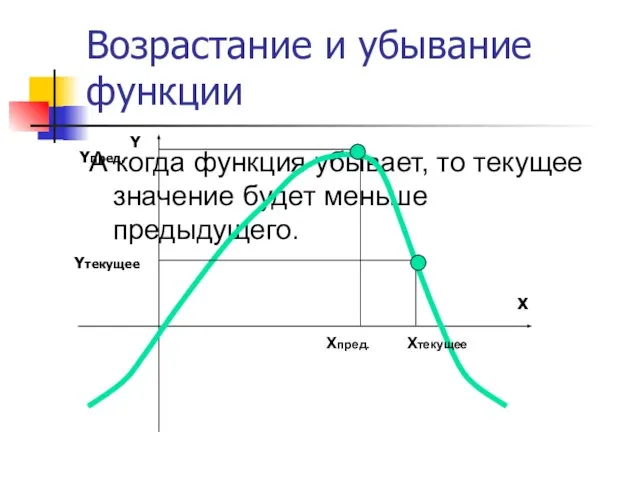
Возрастание и убывание функции
А когда функция убывает, то текущее значение будет меньше предыдущего.
Yпред.
Yтекущее
Xтекущее
Xпред.

Заведем переменную
Возрастание и убывание функции
Yp,
в которой будем запоминать предыдущее значение функции.
Договоримся, что при
зеленого цвета,
а при убывании – линия
желтого цвета.
возрастании графика
будет идти линия, оттеняющая график,

…
k = 10000
FOR x = xmin TO xmax STEP (xmax - xmin) / k
y = f(x)
IF y > 0 THEN CIRCLE (x, y), 2, 4 ELSE CIRCLE (x, y), 2, 1
NEXT x
Возрастание и убывание функции
Тогда, с учетом вышеизложенного, можно подправить предыдущую программу:
yp = f(xmin)
IF y > yp THEN CIRCLE (x, y + 5), 2, 2
IF y < yp THEN CIRCLE (x, y - 5), 2, 14
yp = y

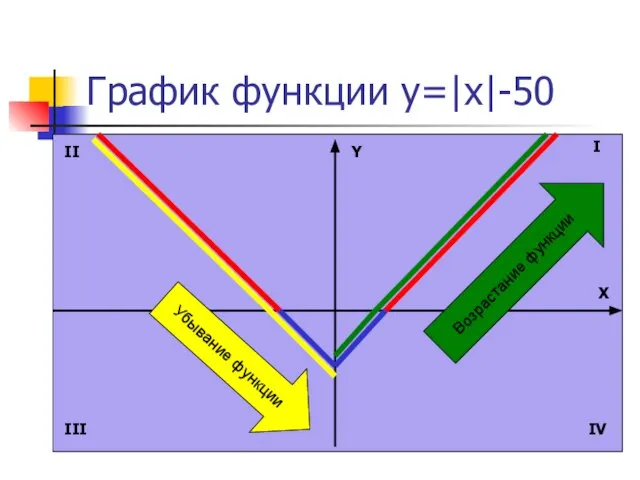
График функции y=|x|-50
Y
X
I
II
III
IV
Убывание функции
Возрастание функции

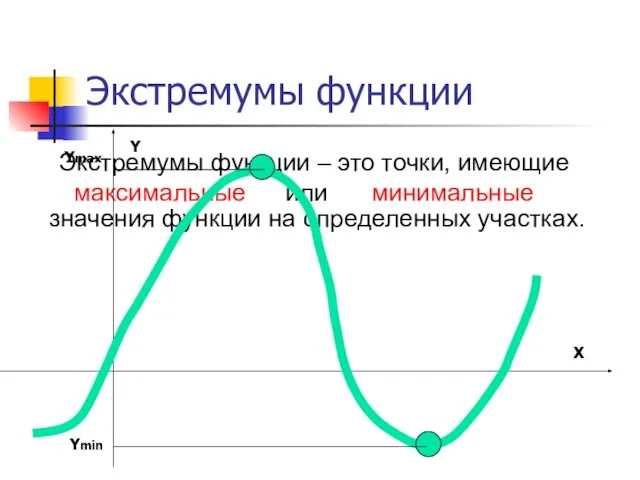
Экстремумы функции
значения функции на определенных участках.
Экстремумы функции – это точки, имеющие
максимальные
или
минимальные
X
Y
Ymax
Ymin

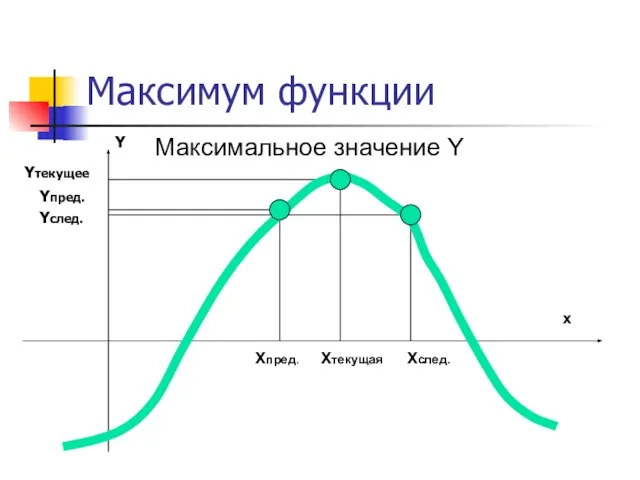
Максимум функции
Xтекущая
Xпред.
Xслед.
Yтекущее
Yпред.
Yслед.
x
Y
Максимальное значение Y

Максимум функции
на этом участке.
То есть, если в текущей точке функция имеет
большее значение
среди значений функций
предыдущей
и
следующей
за ней точками,
то она будет считаться
максимумом функции

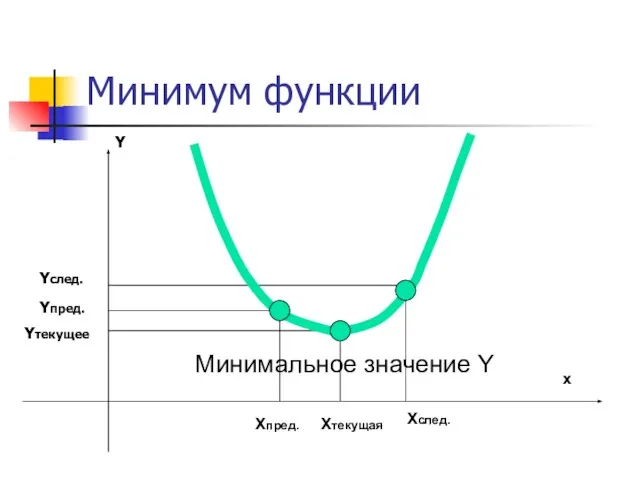
Минимум функции
Xтекущая
Xпред.
Xслед.
Yтекущее
Yпред.
Yслед.
x
Y
Минимальное значение Y

Минимум функции
на этом участке.
То есть, если в текущей точке функция имеет
меньшее значение
среди значений функций
предыдущей
и
следующей
за ней точками,
то она будет считаться
минимумом функции

Тогда с учетом этого и подправим программу – вставим команды рисования точек с экстремальными значениями функции:
Экстремумы функции
…
FOR x = xmin TO xmax STEP (xmax - xmin) / k
y = f(x)
IF y > yp THEN CIRCLE (x, y + 5), 2, 2
IF y < yp THEN CIRCLE (x, y - 5), 2, 14
yp = y
IF y > 0 THEN CIRCLE (x, y), 2, 4 ELSE CIRCLE (x, y), 2, 1
NEXT x
IF y > yp AND y > f(x + (xmax - xmin) / k) THEN CIRCLE (x, y), 10, 4
IF y < yp AND y < f(x + (xmax - xmin) / k) THEN CIRCLE (x, y), 10, 1

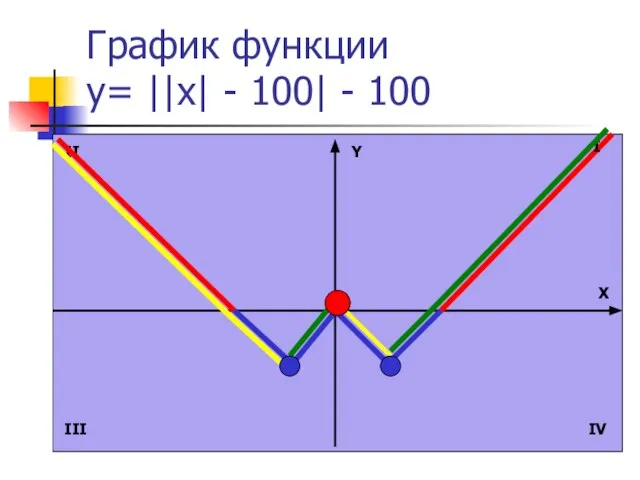
График функции
y= ||x| - 100| - 100
Y
X
I
II
III
IV

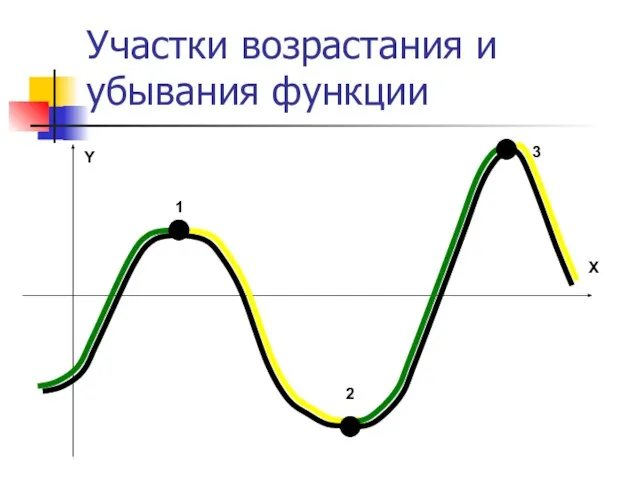
Участки возрастания и убывания функции
1
2
3
X
Y

Участки возрастания и убывания функции
При переходе от максимума к минимуму функция убывает
Выводы: При переходе от минимума к максимуму функция возрастает