StepSRacPoK

Корнем n-й степени из числа а называется такое число х, которое после возведения в n-ю степень дает а.
Арифметическим корнем n—ой степени из неотрицательного числа a называется неотрицательное число, n—ая степень которого равна a.
Подкоренное выражение
Показатель корня
Знак арифметического корня (радикал)
Это определение можно записать так:
Например:
Устно
из 29 слайдов, слайд №

Самостоятельно
из 29 слайдов, слайд №

Корень нечетной степени из положительного числа положителен, из отрицательного—отрицателен, т. е. корень нечетной степени имеет тот же знак, что и подкоренное число.
Корень четной степени из отрицательного числа не существует
Устно
из 29 слайдов, слайд №

Свойства арифметических корней
Свойства корней n—ой степени сходны со свойствами квадратных корней
Но квадратные корни имели одинаковые показатели = 2, поэтому чтобы действовать по аналогии с квадратными корнями мы должны уравнивать показатели корней, т.е. приводить корни к одинаковым степеням. Для этого используется основное свойство корня:
Величина корня не изменится, если показатель степени корня и показатель степени подкоренного выражения умножить на одно и то же число, не равное нулю, т. е.
из 29 слайдов, слайд №

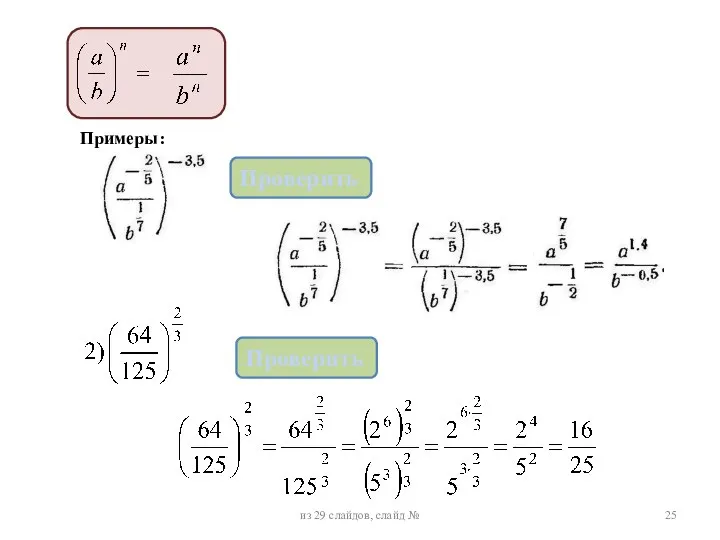
Читая то же самое тождество справа налево, получим:
показатель степени корня и подкоренного выражения можно разделить на их общий делитель.
из 29 слайдов, слайд №

Данное свойство используется для сравнения корней
Приведем корни к одинаковым показателям. Для этого найдем наименьшее из чисел, которое делится и на 6 и на 9 . Это число 18
Приведем корни к одинаковым показателям. Для этого найдем наименьшее из чисел, которое делится и на 4 и на 8. Это число 8.
из 29 слайдов, слайд №

1. Что больше: или ?
2. Что больше:
Самостоятельно
из 29 слайдов, слайд №

Проверьте себя:
из 29 слайдов, слайд №

из 29 слайдов, слайд №
Пример:

Будем рассматривать корень любой степени с a>0. Тогда извлечение корня из чисел можно заменить действием возведения в степень.
Степень с дробным (положительным) показателем есть корень, показатель степени которого равен знаменателю дробного показателя, а подкоренное выражение представляет собой степень того же основания с показателем, равным числителю дробного показателя.
Переход от корня к степени
из 29 слайдов, слайд №

Примеры:
Самостоятельно
Представьте корень в виде степени.
из 29 слайдов, слайд №

Проверьте себя:
из 29 слайдов, слайд №

Под корнем четной степени всегда стоит неотрицательное число.
Под корнем же нечетной степени (2n+1) может стоять любое число, в том числе и отрицательное. В этом случае, чтобы заменить корень на степень минус «-» надо вынести перед корнем.
Примеры:
из 29 слайдов, слайд №

из 29 слайдов, слайд №
Представьте корень в виде степени.
Самостоятельно

из 29 слайдов, слайд №
Проверьте себя:

Примеры:
В общем виде данное свойство выглядит: .
Сравните со свойством степени с целым отрицательным показателем.
А если показатель отрицательный, то
из 29 слайдов, слайд №

1.Сформулируйте определение степени с отрицательным рациональным показателем и запишите его аналитически.
2. Запишите, пользуясь этим определением, следующие степени в виде дробей:
3. Запишите в виде степеней:
Самостоятельно
из 29 слайдов, слайд №

Проверьте себя:
из 29 слайдов, слайд №

Действия над степенями с дробными показателями выполняются по тем же правилам, что и над степенями с любыми целыми показателями, т. е. по правилам:
ат · аn = ат+n
ат : аn= ат-n
(ат)n= ат·n
(аbc)n= аn · bn · cn
из 29 слайдов, слайд №

ат · аn = ат+n
из 29 слайдов, слайд №
Примеры:
Проверить
Проверить
Проверить
4)
Проверить

ат : аn= ат-n
из 29 слайдов, слайд №
Примеры:
4)
Проверить
Проверить
Проверить
Проверить

(ат)n= ат·n
из 29 слайдов, слайд №
Проверить
Проверить
Проверить
Проверить
4)
Примеры:

(аbc)n= аn · bn · cn
Примеры:
из 29 слайдов, слайд №
Проверить
Проверить
2)

Примеры:
из 29 слайдов, слайд №
Проверить
Проверить

1. Можно ли при выполнении действий над степенями с дробными показателями пользоваться правилами действий над степенями с целыми показателями?
Самостоятельно
из 29 слайдов, слайд №
(Сначала производите действия в скобках, десятичную дробь замените на обыкновенную, числа старайтесь представлять в виде степени.)
Основание степени каждого из сомножителей, стоящих в скобках, представьте в виде степени числа 2.
Подсказка
Подсказка
Подсказка
Используйте формулы сокращенного умножения
Не получается? Обратитесь к преподавателю, но покажите свое решение.

Проверьте себя:
из 29 слайдов, слайд №
1. Можно. Правила действий над степенями с целыми и дробными показателями одни и те же.
2.
4. 5

При упрощении следующих примеров, корни замените на степени, составные числа ( 32, 48, 81,16) представьте в виде степени или произведения степеней или простых чисел, и только потом пользуйтесь свойствами степени.
из 29 слайдов, слайд №
Подсказка
Подсказка
Подсказка
1.
2.
3.
4.
Подсказка
Выполните действия в скобках, а затем замените дробь 0,4 на обыкновенную дробь
Самостоятельно
Не получается? Обратитесь к преподавателю, но покажите свое решение.