Тайны паркетов

Почему мне это интересно?
В начале этого учебного года в курсе геометрии мы знакомились с темой «Выпуклые многоугольники». Когда был рассмотрен вопрос о сумме углов выпуклого многоугольника и разобран ряд задач, учитель рассказал нам о том, что эта тема имеет практическое применение и связана с покрытием плоскости паркетами разных видов. Подробно на этом мы не остановились, но этот вопрос меня очень заинтересовал.

Я решил узнать:
Что такое паркет?
Как проверить
собственную
гипотезу?
Каково прикладное значение выбран-ной мной темы ?
Только ли ученые-
математики
занимаются этой темой?
Какие бывают
виды паркетов?
Какими фигурами можно покрыть плоскость?
Какова история паркета?

Я выдвинул гипотезу: паркеты можно составлять только из правильных многоугольников и этих паркетов - конечное множество.
Цель данного проекта:
исследовать вопрос о покрытии плоскости многоугольниками.

Для достижения цели я поставил перед собой следующие задачи:
1) найти источники дополнительной информации
-о истории возникновения паркетов;
-о видах паркетов;
-о многоугольниках, с помощью которых можно составить паркет;
2) провести исследование, выясняющее, насколько верна выдвинутая мной гипотеза;
3) проанализировать, обобщить и систематизировать полученные данные;
4) подобрать иллюстрации и оформить презентацию «Тайны паркетов»;
5) ознакомить с результатами проекта учащихся
7-9 классов на уроках геометрии.

Что такое паркет?
Паркет (франц. parquet)- небольшие древесные, строганные планки для покрытия пола. С XVI в. известен в России. Паркет изготавливают преимущественно из твердых пород дерева, для художественного паркета используют ценные породы.
Паркет – это настил на полу из дощечек, уложенный так, что они образуют какой-нибудь рисунок (словарь С.И.Ожегова);
Паркет – это такое покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину или совсем не имеют общих точек («Энциклопедический словарь юного математика»);
Паркет - бесконечное семейство
многоугольников, покрывающее
плоскость без просветов и двойных
покрытий.

Паркеты из правильных многоугольников
Паркет называется правильным, если он составлен из равных правильных многоугольников и вокруг каждой вершины правильные многоугольники расположены одним и тем же способом.
Если при составлении паркета использовать несколько правильных многоугольников с различным числом сторон, то такой паркет называется полуправильным.

В вершине паркета может сходиться не более шести и не менее трех многоугольников. Действительно, при схождении в одной вершине семи или более многоугольников хотя бы один угол в правильном многоугольнике должен быть менее 60°, что невозможно (минимальный угол — у треугольника — равен 60°).
При схождении в одной вершине двух многоугольников у одного из них внутренний угол должен быть более 180°, что, очевидно, также невозможно. Таким образом, решение задачи распадается на анализ тех вариантов, когда в вершине паркета сходятся 3, 4, 5 и 6 правильных многоугольников.

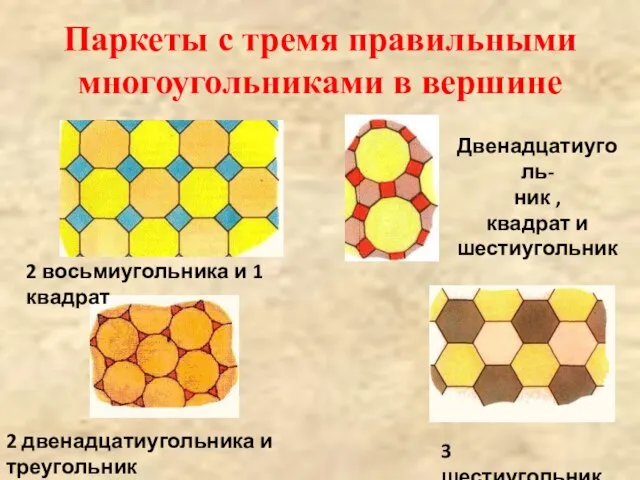
Паркеты с тремя правильными многоугольниками в вершине
3 шестиугольника
2 восьмиугольника и 1 квадрат
Двенадцатиуголь-
ник ,
квадрат и
шестиугольник
2 двенадцатиугольника и треугольник

Паркеты с четырьмя правильными многоугольниками в вершине
4 квадрата
Шестиугольник,
треугольник и
2 квадрата
2 шестиугольника и 2 треугольника

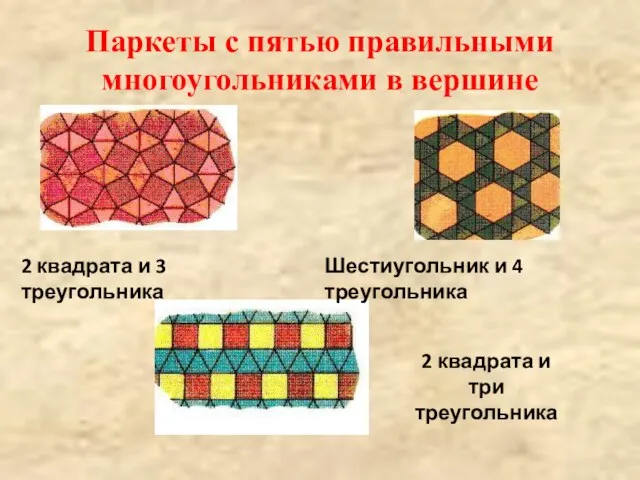
Паркеты с пятью правильными многоугольниками в вершине
2 квадрата и 3 треугольника
Шестиугольник и 4 треугольника
2 квадрата и три
треугольника

Паркеты с шестью правильными многоугольниками в вершине
6 треугольников

Паркеты из неправильных многоугольников
Возьмем произвольный четырех-угольник ABCD (I) и построим симметричный ему относительно середины стороны АВ четырех-угольник(II). Четырехугольник II отразим симметрично относительно середины его стороны ВС (III ). Отразим его симметрично относи-тельно середины стороны CD (IV). Четырехугольники I,II,III,IV примы-кают к общей вершине углами A,B,C,D, которые в сумме дают 360 градусов, поэтому четырехугольники заполнят плоскость вокруг общей вершины.

Паркеты из неправильных многоугольников
Вообще можно покрыть плоскость копиями произвольного многоугольника, необязательно выпуклого:

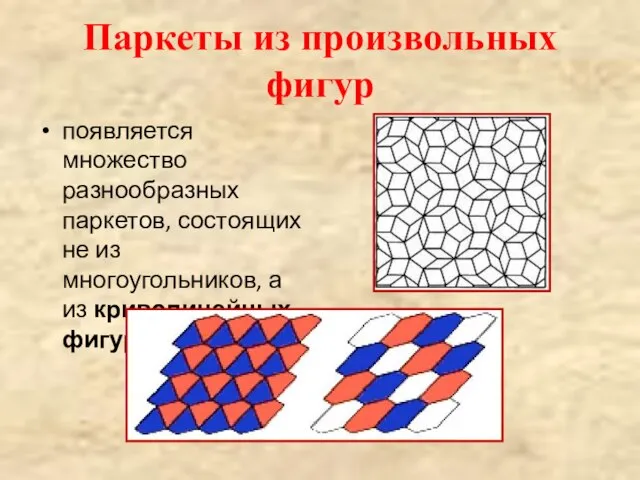
Паркеты из произвольных фигур
появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур

Паркеты из произвольных фигур
Всемирная известность пришла к Эшеру в 1951 году. В 1954 году в Амстердаме состоялась большая выставка Эшера, приуроченная к Международному математическому конгрессу. Математики сразу признали художника «своим»; с этого времени его рисунки – неизменный атрибут физико-математических изданий.
Знаменитый
голландский
художник
Мариус Эшер
(1898-1972).

Наиболее интересными для изучения идеями Эшера являются всевозможные разбиения плоскости.
Регулярное разбиение плоскости, называемое «мозаикой», - это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними. Эшер интересовался всеми видами мозаик, а также ввел собственный вид, который назвал «метаморфозами», где фигуры изменяются и взаимодействуют друг с другом.

Мариус Эшер посвятил орнаментам несколько своих картин.
Среди них: «Всадники», «Летящие птицы»; «Ящерицы».

Способы построения паркетов
Способ первый. Берем некоторую уже известный нам паркет и выполняем преобразования: сжатие или растяжение, замена прямолинейных отрезков кривыми с началом и концом в тех же точках, что и у отрезков...
Пример: паркеты, полученные заменой отрезков "квадратной" сетки некоторыми кривыми или ломаными.

Способы построения паркетов
Способ второй. Объединяем отдельные элементы уже существующих паркетов. Примеры: паркеты, полученные в результате объединения элементов квадратной сетки.

Способы построения паркетов
Способ третий. Берем существующую сетку и дополняем ее новыми линиями. Получаем разбиение плоскости на фигуры, которые затем можно по-новому объединить.

Способы построения паркетов
Способ четвертый. Выбираем некоторую кривую или ломаную и начинаем ее переносить, поворачивать, отражать... получившиеся кривые или ломаные размещаем на плоскости таким образом, чтобы они образовали замкнутые контуры (которые в дальнейшем будут рассматриваться как элементы паркета).

Подводя итоги...
Мне удалось:
- выяснить, что такое паркет с точки зрения математики;
- узнать много нового и интересного об истории возникновения паркетов;
- найти в литературе и в Интернете сведения о том, какие виды паркетов существуют;
провести собственное исследование вопроса о построении паркетов и убедиться в том, что паркетов из правильных многоугольников – конечное число, а именно 11, а также опровергнуть гипотезу о том, что паркеты можно составить только из правильных многоугольников;
подобрать иллюстрации и оформить с помощью руководителя и презентацию «Тайны паркетов»;
- ознакомить с результатами проекта учащихся 7-9 классов.