Тема:«Бросание мяча под определёнными углами к горизонту для попадания в площадную цель»

1. ПОСТРОЕНИЕ И ИССЛЕДОВАНИЕ ФИЗИЧЕСКОЙ МОДЕЛИ

Рассмотрим процесс построения и исследования физической модели движения мячика, брошенного под углом к горизонту.

Постановка задачи.
Необходимо определить скорость и угол бросания мячика для попадания в площадку определенной длины, находящуюся на известном расстоянии.

Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости v0 и угле бросания α значения координат дальности полета x и высоты y от времени можно описать следующими формулами:
(1) x = v0 ·cosα· t
(2) y = v0 ·sinα· t – g·t2/2

Рис. Бросание мячика в площадку
Рис. Бросание мяча в площадку

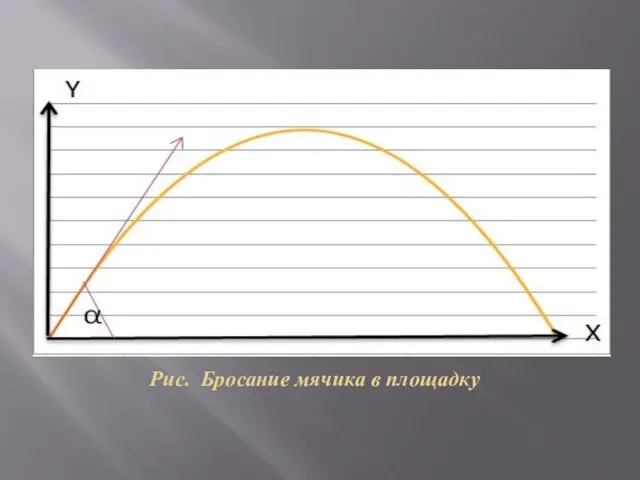
Площадка расположена на поверхности земли, поэтому из формулы (2) можно выразить время,
которое понадобится мячику, чтобы достичь площадки:
v0·sinα·t – g·t2/2 = 0
t·(v0·sinα – g·t/2) = 0

Значение времени t = 0 не имеет физического смысла, поэтому:
v0·sinα – g·t/2 = 0
t = (2·v0·sinα)/g
Подставим полученное выражение для времени в формулу для вычисления координаты х:
x = (v0·cosα·2·v0·sinα)/g = (v02·sin2α)/g

Формализуем теперь условие попадание мячика в площадку. Пусть площадка расположена на расстоянии s и имеет длину l. Тогда попадание произойдет, если значение координаты х мячика будет удовлетворять условию в форме неравенства:
s ≤ x ≤ s + l

Если х < s, то это означает "недолет", а если х > s + l, то это означает "перелет".

2. КОМПЬЮТЕРНАЯ МОДЕЛЬ ДВИЖЕНИЯ МЯЧИКА В ЭЛЕКТРОННЫХ ТАБЛИЦАХ

На основе формальной модели «Бросание мяча в площадку» создадим компьютерную модель с использованием электронных таблиц Excel и OpenOffice Calc.

Выделим в таблице определенные ячейки для ввода значений начальной скорости v0 и угла α и вычислим по формулам (1) и (2) значения координат тела x и y для определенных значений времени t с заданным интервалом.

Электронная таблица

Траектория движения мячика, построенная по электронной таблице

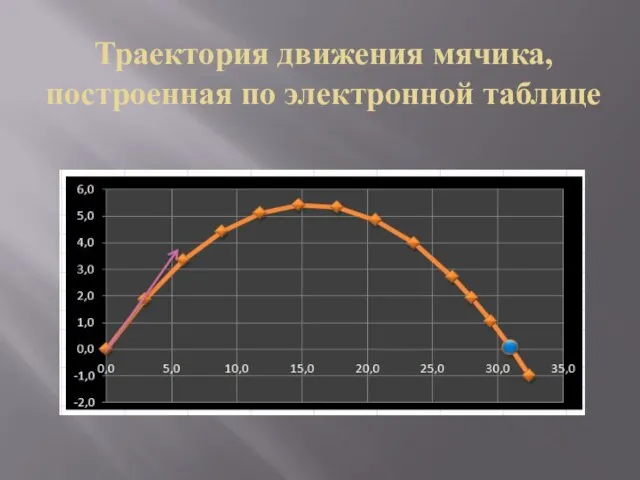
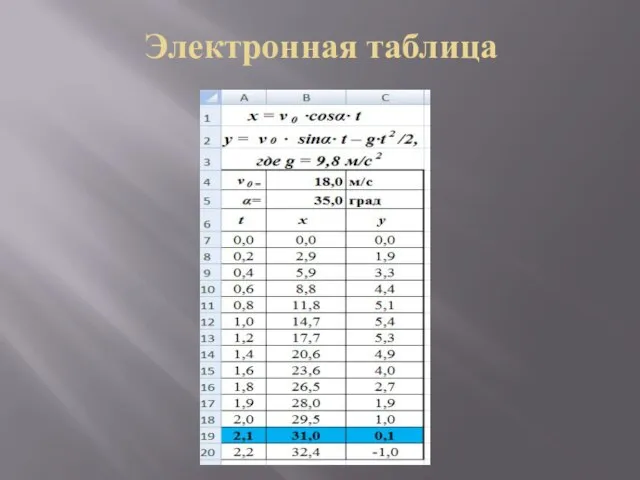
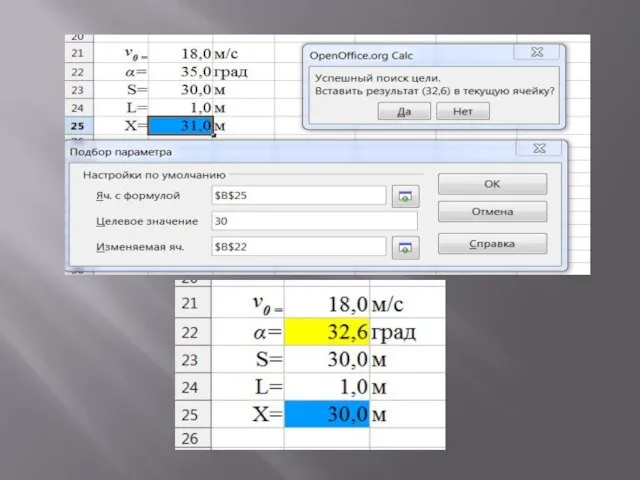
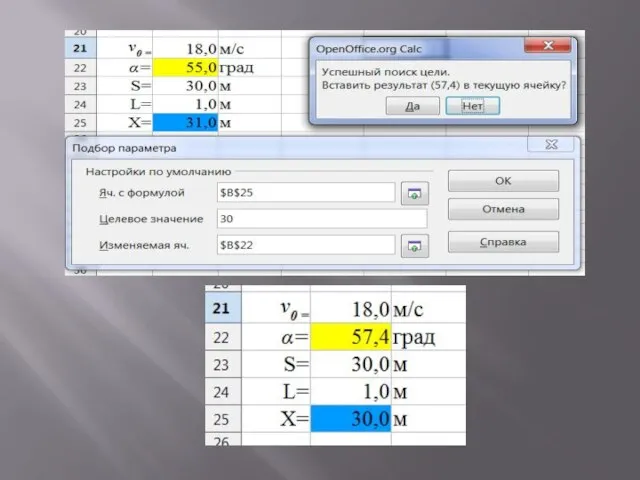
Ниже приведены результаты исследования, полученные методом "Подбор параметров" и зафиксированные снимками с экрана: