Тема: «Исследование функций»

2008г.
Учитель:Юдина Е.В.
Цель урока:
Формировать умение применять полученные сведения для построения графиков функции на основе предварительного исследования функции.

2008г.
Учитель:Юдина Е.В.
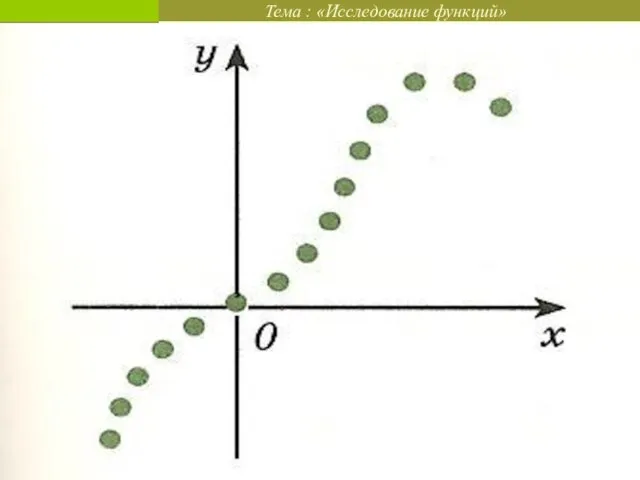
Проверка домашнего задания:
назовите промежутки возрастания и убывания;
назовите точки максимума и минимума;
назовите максимумы и минимумы функции.

2008г.
Учитель:Юдина Е.В.
Изучение нового материала:
Построение графика функции «по точкам» и с ее предварительным исследованием.
Схема исследования функции.
Определения горизонтальной, вертикальной и наклонной асимптот.

2008г.
Учитель:Юдина Е.В.
Закрепление изученного материала:
№ 93; № 94(а, в); № 95(а, б);
№ 96(в)
Замечание к № 95(б): находить абсциссу вершины параболы по формуле в
х0 = - -----
2а

2008г.
Учитель:Юдина Е.В.
Итог урока:
Какие задачи решаются при исследовании функции?

2008г.
Учитель:Юдина Е.В.
Домашнее задание:
§2, п.6 читать; № 94(б, г);
№ 95(в, г); № 96(а).

2008г.
Учитель:Юдина Е.В.
Пример №1

2008г.
Учитель:Юдина Е.В.

2008г.
Учитель:Юдина Е.В.
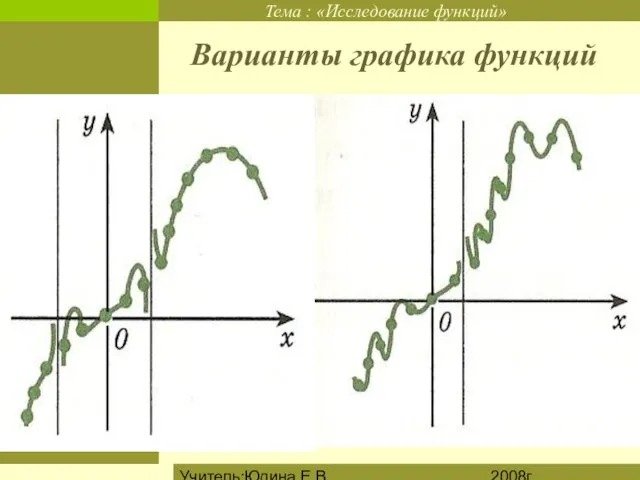
Варианты графика функций

2008г.
Учитель:Юдина Е.В.
Данные о функции ƒ :
D(ƒ): (-∞; - 10), (-10; 10), (10; ∞);
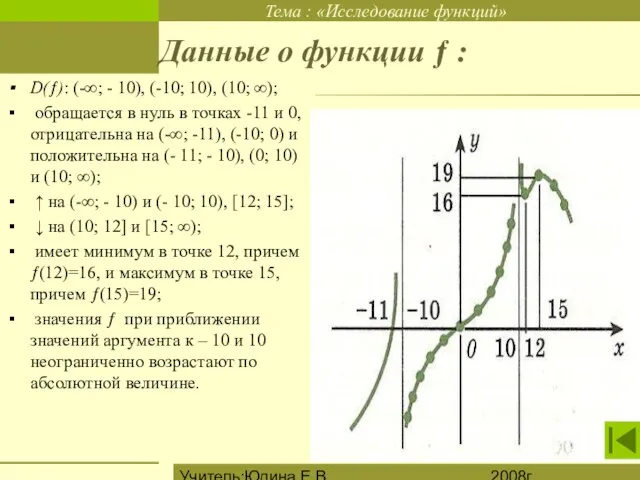
обращается в нуль в точках -11 и 0, отрицательна на (-∞; -11), (-10; 0) и положительна на (- 11; - 10), (0; 10) и (10; ∞);
↑ на (-∞; - 10) и (- 10; 10), [12; 15];
↓ на (10; 12] и [15; ∞);
имеет минимум в точке 12, причем ƒ(12)=16, и максимум в точке 15, причем ƒ(15)=19;
значения ƒ при приближении значений аргумента к – 10 и 10 неограниченно возрастают по абсолютной величине.

2008г.
Учитель:Юдина Е.В.
1
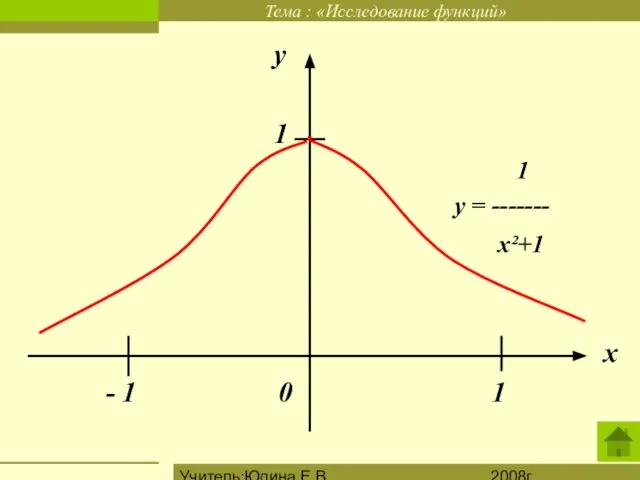
Исследование функций ƒ(х) = ------
х²+1
D (ƒ) = R; 1 1
2. ƒ(-х) = ------- = -------- = ƒ(х) – четная;
(-х)²+1 х²+1
3. График ƒ пересекает:
Оy: (0; ƒ(0)). Значение ƒ(0) = 1. Поэтому график ƒ проходит через точку (0; 1).
1
Оx: ƒ(х) = 0 ; ------- = 0 не имеет корней => не пересекает.
х²+1
4. ƒ(х) > 0 на всей числовой прямой.

2008г.
Учитель:Юдина Е.В.
5. ↑ (-∞; 0], ↓ [0; ∞).
Докажем, что функция ƒ ↓ [0; ∞):
Пусть х1 и х2 – два значения из промежутка [0; ∞), причем х2>х1.
1 1
х1 и х2 – положительны => х2²>х1², х2²+1>х1²+1, ------- < -------
х2>х1 (по условию) х2²+1 х1²+1
=> ƒ(х2)<ƒ(х1), т.е. ↓ на промежутке [0; ∞).
На промежутке (-∞; 0] функция ƒ ↑. Доказательство проводится аналогично. 1
6. Точка 0 – точка максимума функции ƒ(х) = ------; ƒ(0)=1.
х²+1

2008г.
Учитель:Юдина Е.В.
у
1
1
у = -------
х²+1
х
- 1 0 1

2008г.
Учитель:Юдина Е.В.
Схема исследования функций:
1. найти области определения и значений функции.
2. выяснить, является данная функция четной или нечетной; периодической.
3. вычислить координаты точек пересечения графика функции с осями координат.
4. найти промежутки знакопостоянства.
5. найти промежутки возрастания и убывания функции.
6. найти точки экстремума функции и вычислить значения функции в этих точках.
7. построить график функции по известному методу, проводя соответствующие исследования по этому графику.

2008г.
Учитель:Юдина Е.В.
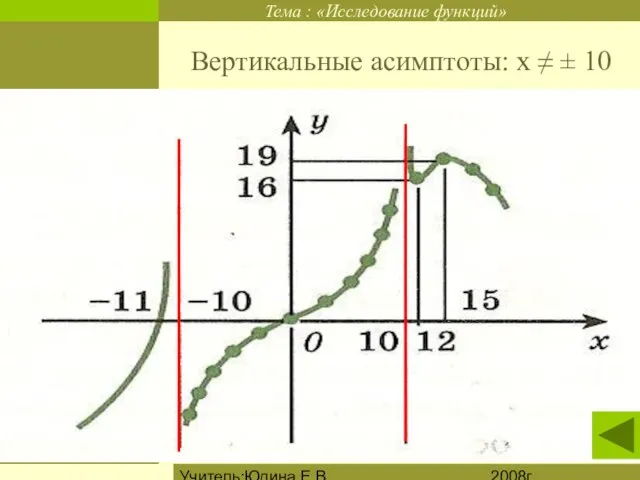
Вертикальные прямые, к которым неограниченно приближается график функции, называют вертикальными асимптотами.
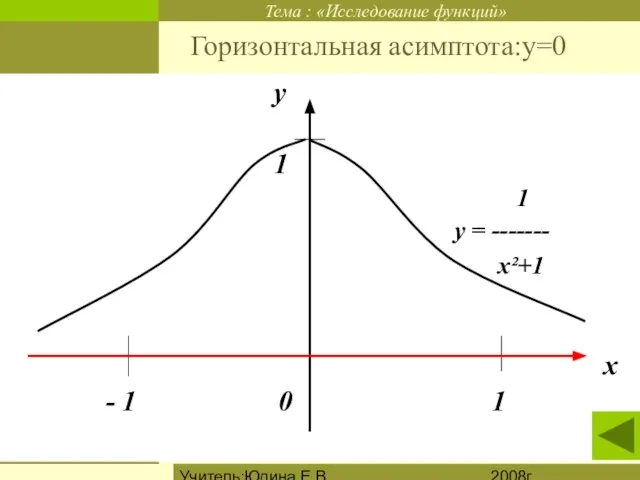
Горизонтальные прямые, к которым неограниченно приближается график функции, называют горизонтальными асимптотами.
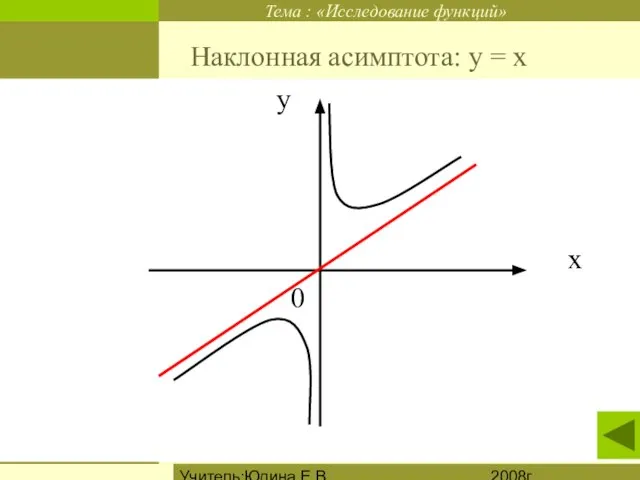
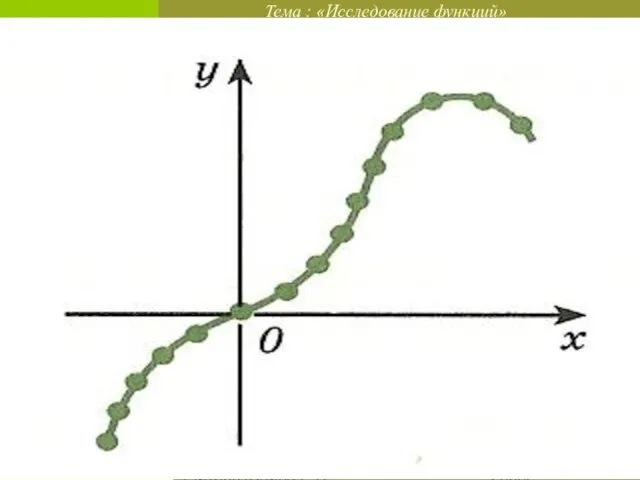
Если график функции неограниченно приближается к некоторой наклонной прямой при неограниченном возрастании х (по модулю), то такую прямую называют наклонной асимптотой.

2008г.
Учитель:Юдина Е.В.
Вертикальные асимптоты: х ≠ ± 10

2008г.
Учитель:Юдина Е.В.
Горизонтальная асимптота:у=0
у
1
1
у = -------
х²+1
х - 1 0 1

2008г.
Учитель:Юдина Е.В.
Наклонная асимптота: у = х
у
х
0