Теорема Пифагора

Биография Пифагора
Пифагор родился в Сидоне, Финикия, около 570 года до нашей эры.
Отец Пифагора, Мнесарх, был достаточно богатым человеком, чтобы дать сыну хорошее воспитание. Когда Мнесарх, отец Пифагора, был в Дельфах по своим торговым делам, он и его жена Партенис решили спросить у Дельфийского оракула, будет ли Судьба благоприятствовать им во время обратного путешествия в Сирию. Пифия (прорицательница Аполлона), не ответила на их вопрос, но сказала Мнесарху, что его жена носит в себе дитя и что у них родится сын, который превзойдет всех людей в красоте и мудрости и который много потрудится в жизни на благо человечества. Мнесарх был столь впечатлен пророчеством, что изменил имя собственной жены на Пифазис в честь Пифийской жрицы. Когда родилось дитя в городе Сидоне, Финикия, оно оказалось, как и говорил оракул, мальчиком. Мнесарх и Пифазис назвали его Пифагором, (в честь Пифии) и посвятили его свету Аполлона.

Пифагор с ранних лет стремится узнать как можно больше. Он обучается в нескольких храмах Греции. Принято считать его первыми учителями Ферекида Сиросского и старца Гермодаманта. Первый прививает мальчику любовь к науке, второй – к поэзии Гомера.
Ряд источников указывает, что Пифагор стал чемпионом одной из первых Олимпиад по кулачному бою.
В юном возрасте Пифагор отправился в Египет, чтобы набраться мудрости и тайных знаний у египетских жрецов. Диоген и Порфирий пишут, что самосский тиран Поликрат снабдил Пифагора рекомендательным письмом к фараону Амасису, благодаря чему он был допущен к обучению и посвящён в таинства, запретные для прочих чужеземцев.
Ямвлих пишет, что Пифагор в 18-летнем возрасте покинул родной остров и, объехав мудрецов в разных краях света, добрался до Египта, где пробыл 22 года (приобщается к математике и создает из нее центр своей философской системы), пока его не увёл в Вавилон в числе пленников персидский царь Камбиз, завоевавший Египет в 525 до н. э. В Вавилоне Пифагор пробыл ещё 12 лет, общаясь с магами, пока наконец не смог вернуться на Самос в 56-летнем возрасте, где соотечественники признали его мудрым человеком.

В Кротоне (Южная Италия) Пифагор основывает школу – пифагорейский союз. Только тех, кто прошел многие ступени знаний, Пифагор называет своими ближайшими учениками и допускает во двор своего дома, где беседует с ними. Отсюда пошло понятие «эзотерический», то есть находящийся внутри.
Пифагорейцы занимаются геометрией, математикой, гармонией, астрономией. Пифагор одним из первых заявляет, что Земля имеет форму шара, а Солнце, Луна и прочие планеты имеют собственную траекторию движения.
В возрасте примерно 60 лет Пифагор женится на Феано, одной из своих учениц. У них рождается 3 детей (два сына и дочь), и все они становятся последователями своего отца.
Пифагор принимает большое участие в политической жизни Кротона. По его инициативе создается аристократический правящий орган – «Совет трехсот». Пифагор сам возглавляет его в течение примерно 25 лет. Постепенно «Совет трехсот» распространяет свое влияние и на соседние города.
Примерно в 500 году до нашей эры в Сибарисе вспыхивает восстание против правления аристократической партии. Поговаривают, что поводом послужил отказ Пифагора принять в свою школу некого богатого, но недостойного гражданина, а тот из мести спровоцировал бунт. После восстания начинаются гонения на пифагорейцев.

О смерти Пифагора известно мало, существует как минимум три версии ухода великого ученого. Несомненно одно – это случилось из-за преследования пифагорейцев. По сохранившимся данным, Пифагор прожил около 100 лет. Воспоминания о Пифагоре дошли до нас благодаря тем немногим его ученикам, которым удалось бежать из Южной Италии в Грецию.
К последователям Пифагора и его учения относили себя Алкмеон, Парменид, Платон, Евклид, Эмпедокл, Кеплер
В III- IV вв. до н. э. появилась компилляция высказываний Пифагора, известная под названием «Священное слово», из которой позднее возникли так называемые «Золотые стихи».
Заключительный отрывок из «Золотых стихов» в переводе И. Петер:
Ты же будь твёрдым: божественный род присутствует в смертных,
Им, возвещая, священная всё открывает природа.
Если не чуждо это тебе, ты наказы исполнишь,
Душу свою исцелишь и от множества бедствий избавишь.
Яства, сказал я, оставь те, что я указал в очищеньях
И в избавленье души ко всему подходи с размышленьем
И руководствуйся подлинным знанием — лучшим возничим.
Если ты, тело покинув, в свободный эфир вознесёшься,
Станешь нетленным, и вечным, и смерти не знающим богом.

Исторические факты
Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:
"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".
В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

Кантор (крупнейший немецкий историк математики) считает, что равенство
3 ² + 4 ² = 5²
было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).
По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

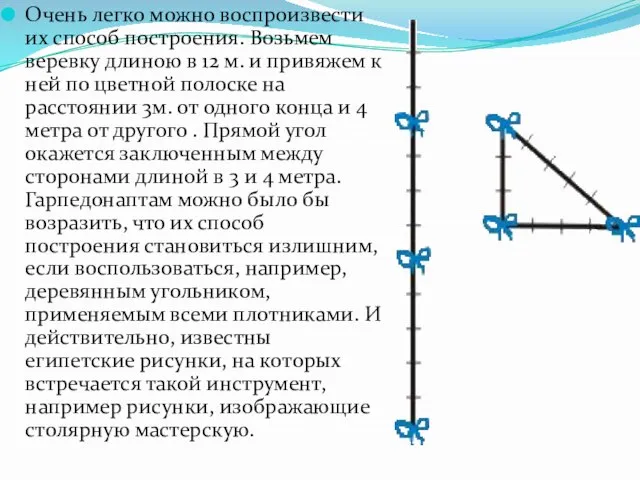
Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.

Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой-на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод:

"Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."
Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.

Формулировки теоремы
Приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.
У Евклида эта теорема гласит (дословный перевод):
"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".
Латинский перевод арабского текста Аннаирици (около 900 г. до н. э. ), сделанный Герхардом Клемонским (начало 12 в.), в переводе на русский гласит:
"Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".

В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так :
"Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".
В первом русском переводе евклидовых "Начал", сделанном Ф. И. Петрушевским, теорема Пифагора изложена так:
"В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".

В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифатор первым дал ее полноценное докзательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Многим известен сонет Шамиссо:

Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвопринашенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя ,вслед.
Они не в силах свету помешать ,
А могут лишь закрыв глаза дрожать
От страха, что вселил в них Пифагор.

Применение теоремы
Рассмотрим примеры практического применения теоремы Пифагора. Не будем пытаться привести все примеры использования теоремы - это вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой. Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур на плоскости.
Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом,
d=2a,
откуда:
d=2a².

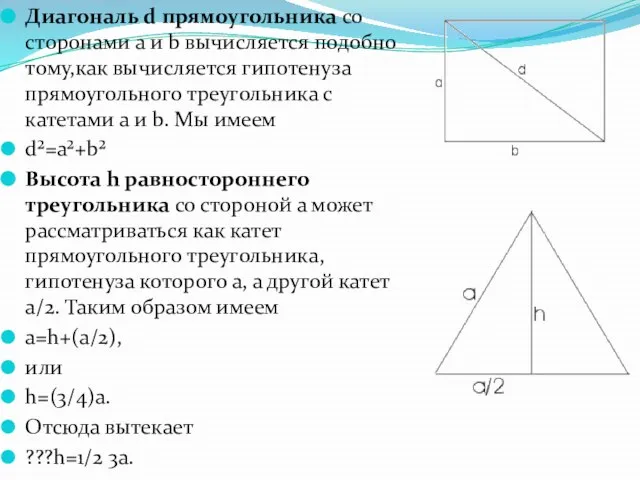
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем
d²=a²+b²
Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а другой катет a/2. Таким образом имеем
a=h+(a/2),
или
h=(3/4)a.
Отсюда вытекает
???h=1/2 3a.

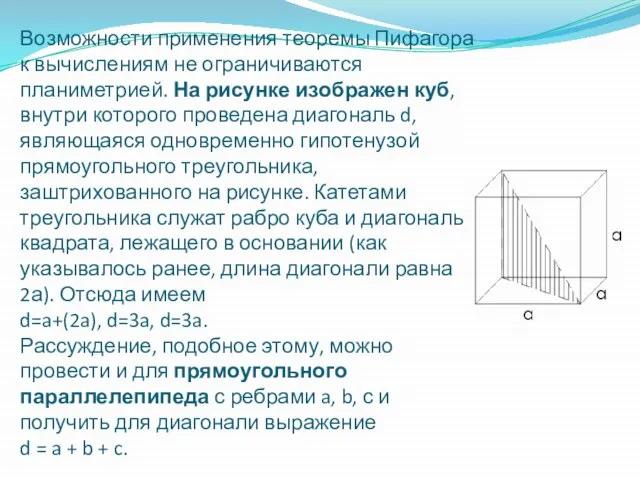
Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат рабро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна 2а). Отсюда имеем
d=a+(2a), d=3a, d=3a.
Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить для диагонали выражение
d = a + b + c.

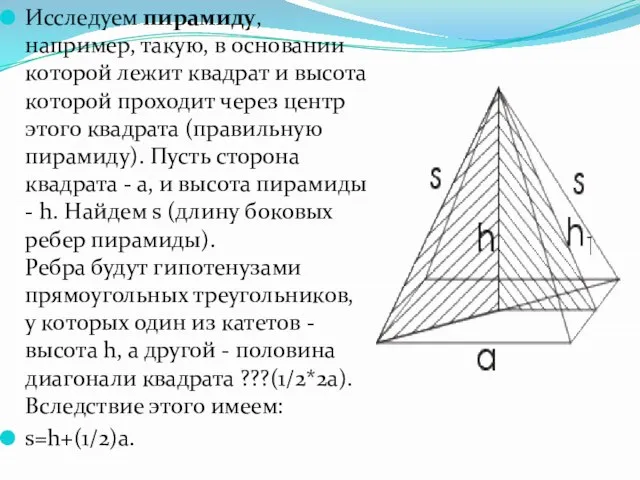
Исследуем пирамиду, например, такую, в основании которой лежит квадрат и высота которой проходит через центр этого квадрата (правильную пирамиду). Пусть сторона квадрата - а, и высота пирамиды - h. Найдем s (длину боковых ребер пирамиды).
Ребра будут гипотенузами прямоугольных треугольников, у которых один из катетов - высота h, а другой - половина диагонали квадрата ???(1/2*2a). Вследствие этого имеем:
s=h+(1/2)a.

Затем можем вычислить высоту h1 боковых граней.
h1= h+(1/4)a.
Считать эти приложения теоремы Пифагора только теоретическими - большая ошибка. Если, например, рассматривать нашу четырехугольную пирамиду как крышу башни, то в первом нашем вопросе речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши, а вопрос о величине боковой поверхности должен интересовать, например, кровельщика при подсчете стоимости кровельных работ. Заметим, что расчет площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит:

«Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила ??? на перекрываемую площадь.»

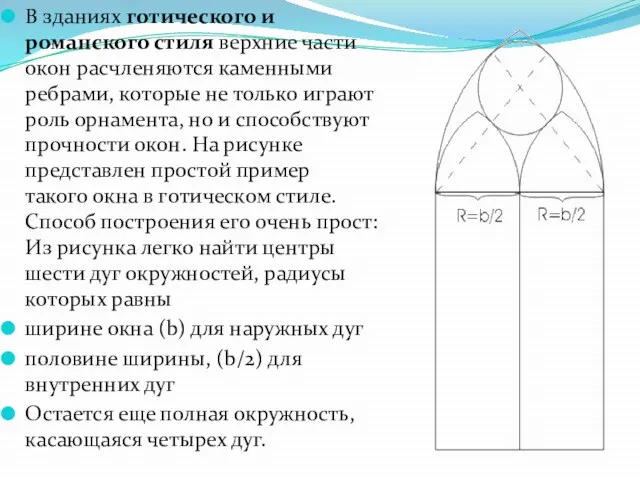
В зданиях готического и ромaнского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: Из рисунка легко найти центры шести дуг окружностей, радиусы которых равны
ширине окна (b) для наружных дуг
половине ширины, (b/2) для внутренних дуг
Остается еще полная окружность, касающаяся четырех дуг.

Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра.
В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоватися вычисления; покажем, как применяется в таких задачах теорема Пифагора.
В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем:
(b/4+p)=( b/4)+( b/4-p)
или
b/16+ bp/2+p=b/16+b/4-bp+p,
откуда
bp/2=b/4-bp.
Разделив на b и приводя подобные члены, получим:
(3/2)p=b/4, p=b/6.

У египтян была известна задача о лотосе. "На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну."
В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы которые долгое время считались исскуственными) и др.